Using Number Lines for Addition and Subraction

Using the Number Line to do Addition

The number line (or your ruler) is a very useful tool for solving addition problems. Let's have a look at an example so that we can see what to do.

Suppose you want to find the answer to the addition problem, \(4 + 5\).

1. Draw a number line (or take out your ruler).
2. Put your finger down on \(4\) on the number line (or ruler).
3. Move your finger across the number line (or ruler) \(5\) places to the right.
4. The number your finger lands on is the answer.

Let's see this on the number line:

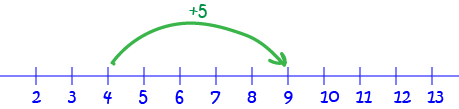
We end up at \(9\), so \(4 + 5 = 9\).

Well, you might have been able to do that one in your head. Let's try some harder problems.

For example, use the number line to find \(2 + 9\).

This time, we'll start at \(2\) and move our finger \(9\) spaces to the right:

We end up at \(11\). So, \(2 + 9 = 11\).

Let's try another. This time we want to know what \(3 + 8\) is. We'll start with our finger on \(3\) and move it \(8\) places to the right:

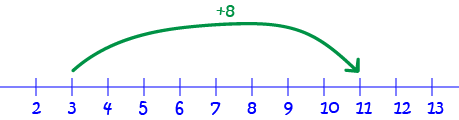
We end up at \(11\). So, \(3 + 8 = 11\).

Finally, let's do the trickiest one yet. What is \(17 + 4\) equal to?

This time, we'll need to start a bit further down the number line at \(17\). You'll have to do some more drawing if you're using a number line. Otherwise, find \(17\) on your ruler. Move your finger along \(4\) places to the right:

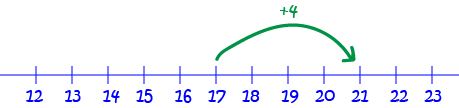
We end up at \(21\). So, \(17 + 4 = 21\).

So that's how we use a number line (or a ruler) to do addition. Let's see how we use a number line to do subtraction. Then we should be able to help Gus.

Using the Number Line to do Subtraction

The number line (or your ruler) is a very useful tool for solving subtraction problems. Let's have a look at an example so that we can see what to do.

Suppose you want to find the answer to the subraction problem: \(8 - 5\)

1. Draw a number line (or take out your ruler).
2. Put your finger down on \(8\) on the number line (or ruler).
3. Move your finger across the number line (or ruler) \(5\) places to the left.
4. The number your finger lands on is the answer.

Let's see this on the number line:

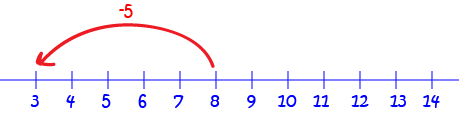
We end up at \(3\), so \(8 - 5 = 3\).

Notice that we move to the left for subtraction and to the right for addition.

Well, you might have been able to do the last example in your head. Let's try some harder problems.

For example, use the number line to find \(13 - 2\).

This time, we'll start at \(13\) and move our finger \(2\) spaces to the left:

We end up at \(11\). So, \(13 - 2 = 11\).

Let's try another. This time we want to know what \(12 - 4\) is. We'll start with our finger on \(12\) and move it \(4\) places to the left:

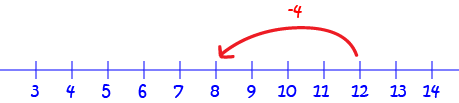
We end up at \(8\). So, \(12 - 4 = 8\).

Finally, it's time to help Gus. Gus needs to find the answer to \(21 - 7\) so that he can work out how many cabbages those pesky caterpillars ate.

This time, we'll need to start a bit further down the number line at \(21\). You'll have to do some more drawing if you're using a number line. Otherwise, find \(21\) on your ruler. Move your finger along \(7\) places to the left:

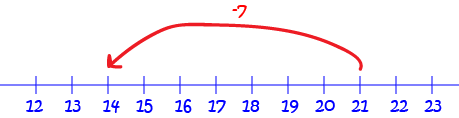
We end up at \(14\). So, \(21 - 7 = 14\), and those pesky caterpillars have eaten \(14\) of Gus' cabbages. Poor Gus!

Footnote (taking too much away)

Sometimes, when we do subtraction, we try to take away something bigger than the number we are subtracting from. The answer will be one of the minus numbers. Don't worry if you haven't heard of them. It's good to know that they exist, but you won't need to do anything with them for a while yet. If you're curious and want to find out more about the minus numbers, have a look at the article on the negative numbers.

Let's just see what happens if we use a number line to work out the answer to \(2 - 3\):

If we start at \(2\) and move three places to the left, we go past \(0\) and end up at \(-1\), which is one of the minus numbers. So, \(2 - 3 = -1\).