Commutative, Associative and Distributive Laws

These laws for addition and multiplication sound very complicated, but they are really very simple to use and remember.

Commutative Laws

The Commutative Law for Addition

The commutative law for addition says that order doesn't matter when you are adding. If \(a\) and \(b\) are numbers, then the commutative law for addition says that

For example,

So, \(2 + 5 = 7 = 5 + 2\).

The Commutative Law for Multiplication

There's also a commutative law for multiplication. It says that, whenever \(a\) and \(b\) are numbers, then

The pictures below give examples of the commutative laws for both addition and multiplication

The top sum with apples shows that \(3 + 2 = 5 = 2 + 3\). The bottom sum with applies shows that \(3 \times 2\) is the same as \(2 \times 3\). They are both \(6\).

It's hard to remember long words like "commutative", but if you think of commuters travelling to and from work on the train, it might help you. They travel in both directions as well.

Associative Laws

There are "associative laws" for both addition and multiplication as well. They say that the way we group numbers together doesn't matter when we're multiplying or adding them. If \(a,b\) and \(c\) are numbers, then the associative law for addition says that

For example,

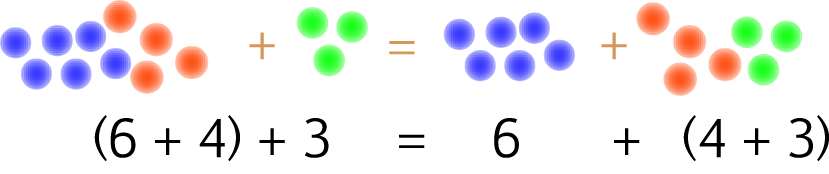
shows that \((6 + 4) + 3 = 13 = 6 + (4 + 3)\). If \(a,b\) and \(c\) are numbers, then the associative law for multiplication says that

For example,

shows that \((2 \times 5) \times 3 = 30 = 2 \times (5 \times 3)\).

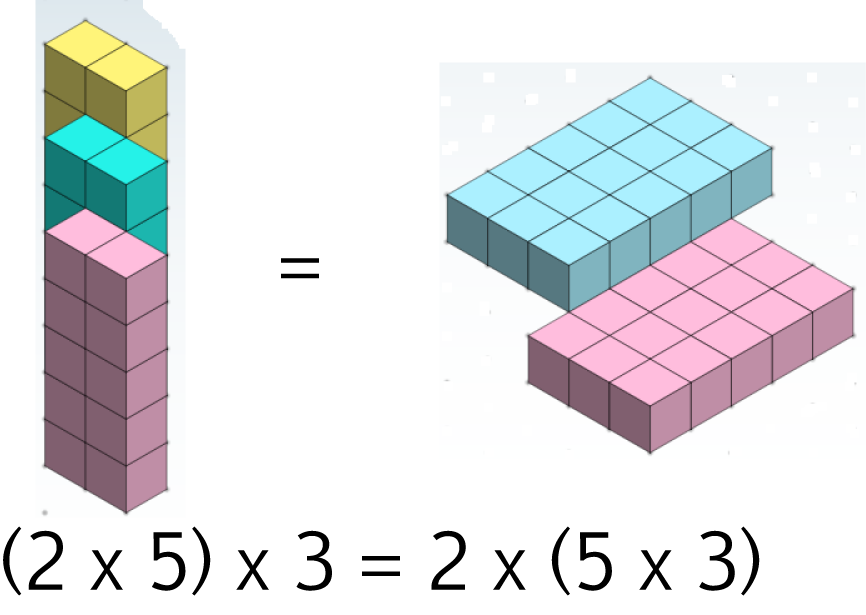
Together, the associative and commutative laws for addition and multiplication can really help you to simplify calculations. Sometimes it's easier to add or multiply in a different order.

For example, if you need to find \(23 + 18 + 7\), it's easier to calculate \((23 + 7) + 18 = 30 + 18 = 48\). The associative and commutative laws allow you to do just that.

In multiplication, you might be asked to calculate \(5 \times (23 \times 2)\). The commutative law for multiplication tells you that this is the same as \(5 \times (2 \times 23)\), and the associative law for multiplication tells you that this is the same as \((5 \times 2) \times 23 = 10 \times 23 = 230\), which is much easier to compute.

The Distributive Law

The Distributive Law tells you how to combine multiplication and addition. It lets you "distribute" multiplication over addition. If \(a,b\) and \(c\) are numbers, then the distributive law states that

For example,

shows that \(4 \times (2 + 3) = 4 \times 5 = 20 = 8 + 12 = 4 \times 2 + 4 \times 3\).

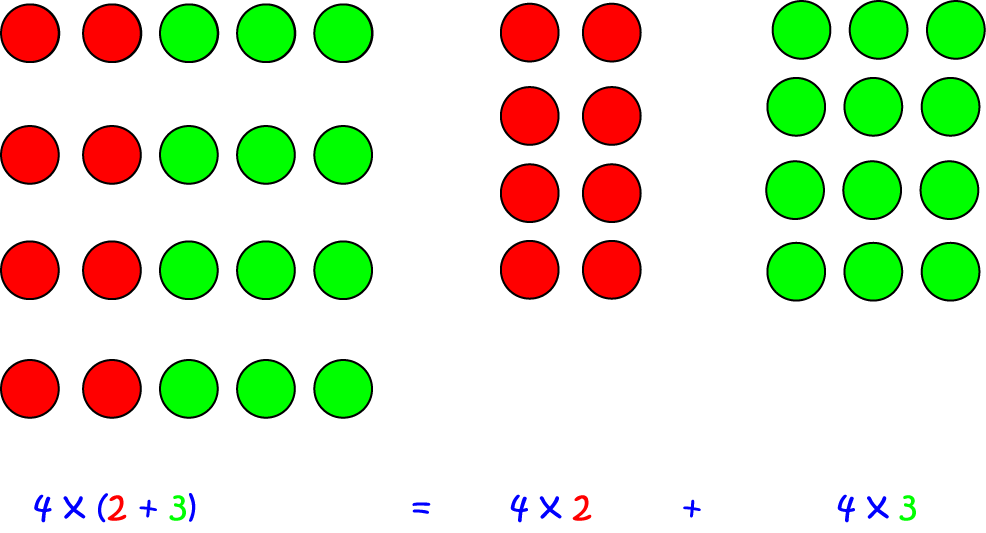
The distributive law comes in very handy when you need to do difficult multiplications. For example, \(8 \times 307 = 8 \times (300 + 7) = 8 \times 300 + 8 \times 7 = 2,400 + 56 = 2,456\).

You can also use the distributive law in reverse, to combine two more difficult sums into one easier one. For example, \(6 \times 17 + 6 \times 3 = 6 \times (17 + 3) = 6 \times 20 = 120.\)

We can also use the distributive law for subtraction because \(a - b\) is the same as \(a + (-b)\). So, for example, \(5 \times 28 - 5 \times 26 = 5 \times (28 - 26) = 5 \times 2 = 10\).

Finally, you can apply the distributive law over and over again to add a long list of products. For example, \(5 \times 3 + 2 \times 3 + 1 \times 3 + 2 \times 3 = (5 + 2 + 1 + 2) \times 3 = 10 \times 3 = 30.\)

Conclusion

If \(a,b\) and \(c\) are numbers, then

• The commutative laws state that:
  \(\begin{eqnarray*} a + b &= b + a\\ a \times b &= b \times a \end{eqnarray*} \)
• The associative laws state that
  \(\begin{eqnarray*} (a + b) + c &= a + (b + c)\\ (a \times b) \times c &= a \times (b \times c) \end{eqnarray*} \)
• The distributive law states that
  \(\begin{eqnarray*} a \times (b + c) &= a \times b + a \times c \end{eqnarray*} \)

We need to be very careful when we apply these laws. The commutative and associative laws don't work for division and subtraction. For example, \(6 \div 3 = 2\), but \(3 \div 6 = \dfrac{1}{2}\) and \( (7 - 5) - 2 = 2 - 2= 0\), but \(7 - (5 - 2) = 7 - 3 = 4\).

The distributive law does work for subtraction, but it does not work for division. For example, \(36 \div (3 + 9) = 36 \div 12 = 3\), but \(36 \div 3 + 36 \div 9 = 12 + 4 = 16\).

It is a great idea to remember these laws. They can make your life so much easier. But remember, wearing your undies on the outside of your tights is not a good look, even for super heroes!