Prekinder to Grade 2 Mathematics
Lines of Symmetry of Plane Shapes
Lines of Symmetry of Plane Shapes
It's getting pretty close to Christmas now. One of the things I like to do at Christmas time is make gingerbread. However, it's been really hot lately, and I use a Swedish recipe for my gingerbread that relies on the weather being cool. Today was forecast to be a lot cooler, so I mixed up my gingerbread dough last night, put it in the fridge and got up early this morning to make the biscuits. I have a collection of cutters in all different shapes and sizes. Some of them, like the gingerbread man cutter and the star cutter are quite symmetrical. Others like the poor old wombat are not.
I've added some dotted lines on the star and gingerbread man in the picture. Do you see how you could cut the two shapes into two equal halves along each of these lines? These lines are called
lines of symmetry (or axes of symmetry).
You should be able to fold a plane shape along its lines of symmetry and find that the two halves of the shape match each other exactly. You probably don't want to do this with a gingerbread man: the two halves would stick together and you wouldn't be able to bake him, but the idea is that they should cut him into two equal halves.

Let's investigate the lines of symmetry of some plane (flat) shapes.
Folding a Plane Shape to Check for Lines of Symmetry
You can find out if a line is a line of symmetry for a plane shape by folding the shape along that line. If the two halves of the shape match up perfectly, then the line that you folded along is a line of symmetry. If not, it isn't. Let's see this in action on a trapezium.
First, we'll fold the trapezium along a horizontal line that cuts through the sloping sides of the trapezium:

Can you see how the sloping sides of the trapezium don't match up? In fact, there's quite a bit of the lower part of the trapezium sticking out from under the upper part. So, this fold line is definitely not a line of symmetry.
When we try to fold the trapezium along a vertical line that cuts its two horizontal sides in half, the two parts match up perfectly, with no overlap. So, this vertical line is a line of symmetry.
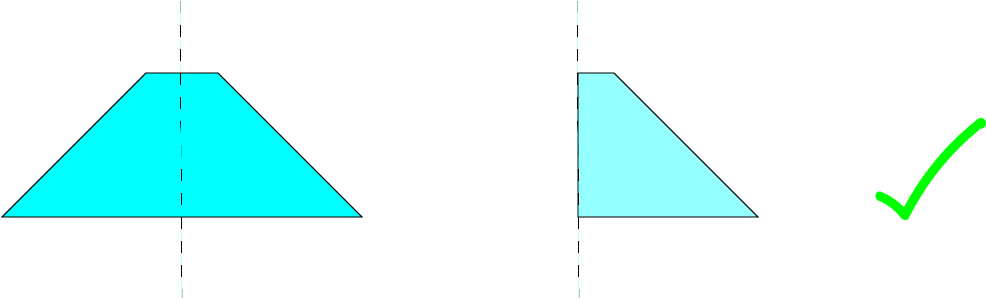
Lines of Symmetry in Plane Shapes
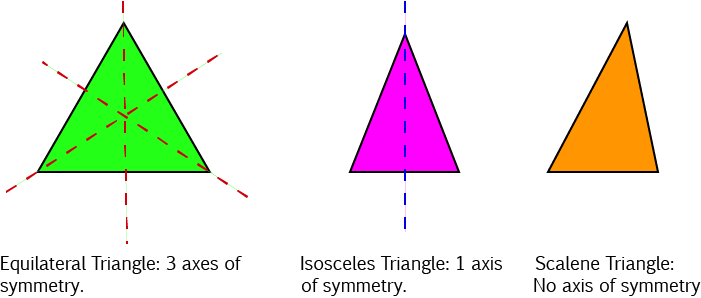
Triangles
As triangles can have three equal sides, two equal sides, or no equal sides, they can have three, one or no lines of symmetry as shown in the pictures below:
Quadrilaterals
There are many different types of quadrilaterals (four-sided plane shapes). Quadrilaterals can have \(0\), \(1\), \(2\) or \(4\) line of symmetry as shown in the pictures below:
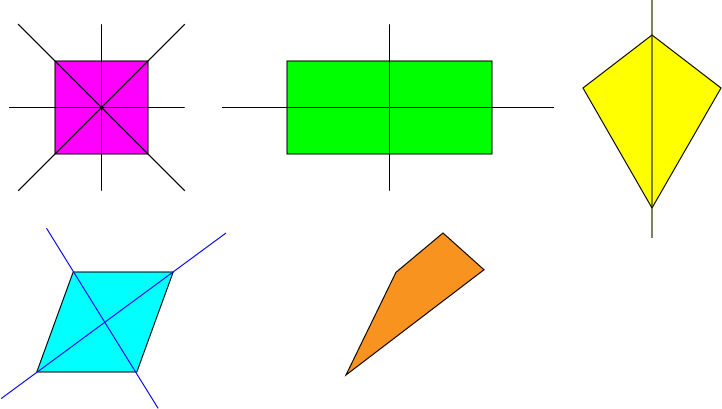
The square (purple) has four equal sides and four lines of symmetry, while the rectangle has two pairs of equal sides and only two lines of symmetry. The kite (yellow) has only only line of symmetry. The rhombus (pale blue) has only two lines of symmetry because its angles are not all equal. All sides of the orangey-brown quadrilateral have different lengths, so it has no lines of symmetry.
So far, we've seen that the regular polygons (equilateral triangle and square) have as many lines of symmetry as they have sides. Let's have a look at more regular polygons and see if the pattern continues.
Regular Polygons
All of the sides and angles of a regular polygon are equal. Let's check how many lines of symmetry each regular polygon has:
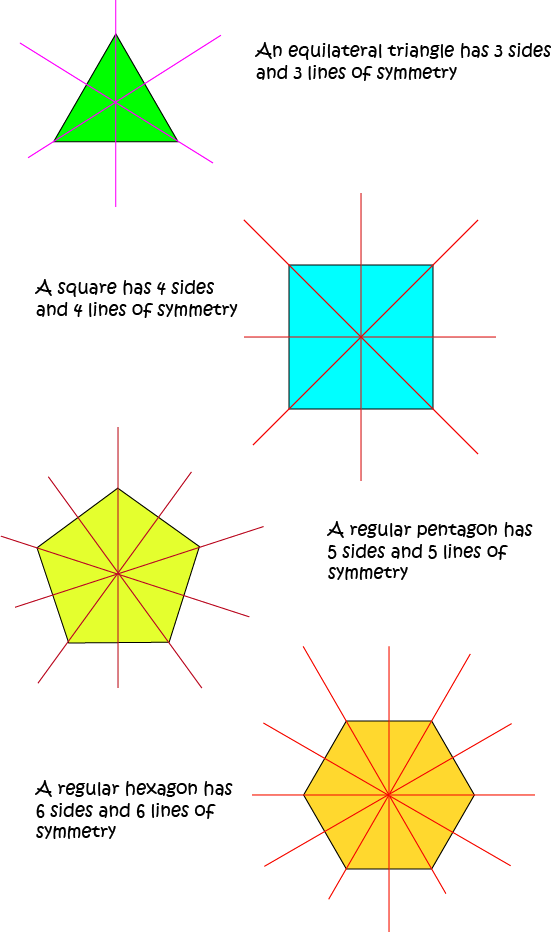
It looks like the pattern continues, so
- A regular heptagon has 7 equal sides and 7 lines of symmetry.
- A regular octagon has 8 equal sides and 8 lines of symmetry.
- A regular nonagon has 9 equal sides and 9 lines of symmetry.
- A regular decagon has 10 equal sides and 10 lines of symmetry.
- ...
- A regular \(n\)-gon will have \(n\) equal sides and \(n\) lines of symmetry.
Now, what about plane shapes that aren't polygons?
Circles

Every diameter (line passing from one point on the circle, through the centre, and cutting it at the other side) of a circle cuts it into two equal semicircles. So, every diameter of a circle is a line of symmetry. A circle has infinitely many diameters, so it has infinitely many lines of symmetry.
Ellipses

There are only two lines that you can draw through the centre of an ellipse that will cut it in half. So, an ellipse has only two lines of symmetry.
Conclusion
Why don't you have a look at some plane shapes and see if you can work out how many lines of symmetry they have? It's lots of fun. You could also try to figure out how many lines of symmetry this beautiful mandala has:

Description
This mini book covers the core of Math for Foundation, Grade 1 and Grade 2 mathematics including
- Numbers
- Addition
- Subtraction
- Division
- Algebra
- Geometry
- Data
- Estimation
- Probability/Chance
- Measurement
- Time
- Money
- and much more
This material is provided free of cost for Parent looking for some tricks for their Prekinder, Kinder, Prep, Year 1 and Year 2 children
Audience
Grade 1/Year 1, Grade 2/Year 2, Prep, Foundation, Kinder and Pre-Kinder
Learning Objectives
These lessons are for kids aged 4-8 with the core objective to expose their brains to concepts of addition, subtraction, division, algebra and much more.
Author: Subject Coach
Added on: 6th Apr 2018
You must be logged in as Student to ask a Question.
None just yet!