Common Number Patters

There are a number of interesting number patterns that crop up all the time. In this article we are going to look at the ones that you see most often, and how they are formed.

If you look at the heights that Timmy has recorded in his table, you might notice that they form a number pattern:

Each number is \(20\) more than the one before it. The sequence of heights that Timmy has reached forms a special kind of number pattern called an Arithmetic Sequence. You might see it called an arithmetic progression in some books.

Arithmetic Sequences

Just like the sequence of heights that Timmy the Turtle has reached, an arithmetic sequence is made by starting with one number, and adding the same amount to it at each step.

For example, the sequence

is made by starting with \(1\) and adding \(2\) over and over again to get the other numbers in the sequence, like this: You can make the pattern as long as you like by keeping going, and adding \(2\) again and again.

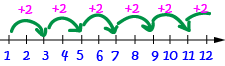
If you want to work out how much is being added each time in an arithmetic sequence, subtract one term from the next term in the sequence. The difference will always be the same.

For example, the sequence

is an arithmetic sequence. To work out how much is added each time, look at the value of \(5 - 2 = 8 - 5 = 3\). The pattern can be continued by adding \(3\) to the last number you've found each time, like this:

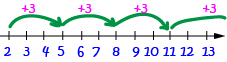
The value that we add to the last term each time is called the common difference: "difference" because you can work it out by subtracting each term from the next term in the sequence, and "common" because the answer is the same all the time.

For example, in the sequence

the common difference is \(27-18 = 9\).

Note that the common difference doesn't have to be a positive number. In the sequence,

the common ratio is \(26 - 28 = -2\), which is negative. So, we find the next term in the sequence by subtracting \(2\).

Geometric Sequences

Geometric sequences are number patterns in which the terms are formed by starting with a number, and multiplying it by the same number over and over again.

For example, the sequence

is formed by multiplying \(1\) by \(4\) again and again. You can keep making more terms of the pattern by multiplying the last term by \(4\), then the term you get by \(4\), then ..., as shown on the number line below:

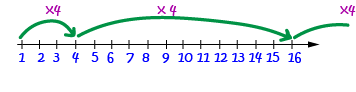
The number that we multiply the last term by each time is called the common ratio. In the last example, the common ratio was \(4\):

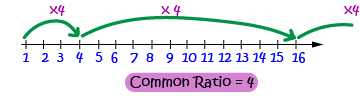
For example, the sequence

starts at \(3\) and has a common ratio of \(2\):

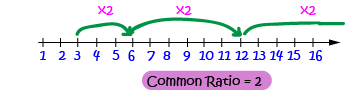
Note:The common ratio does not have to be a whole number. For example, in the sequence

the common ratio is \(\dfrac{1}{2}\).

The common ratio can also be a negative number. For example, you can build a sequence by starting at \(3\) and multiplying by the common ratio \(-2\) to get

However, if the common ratio is \(0\), the sequence is a bit boring. For example,

Special Number Patterns

There are a lot of number patterns around that aren't arithmetic or geometric sequences. Here are some examples.

Triangular Numbers

The numbers are called the triangular numbers. The numbers in this sequence form a pattern of dots that can be arranged as a triangle. You form each additional triangular number by adding an extra row to the previous triangle, and counting the number of dots in the new triangle:

Square Numbers

The numbers form a number pattern consisting of the squares of the whole numbers. For example, \(2 \times 2 = 4\) and \(3 \times 3 = 9\). You can also represent the numbers in this pattern by arranging dots in squares (or using blocks arranged in squares) as shown below:

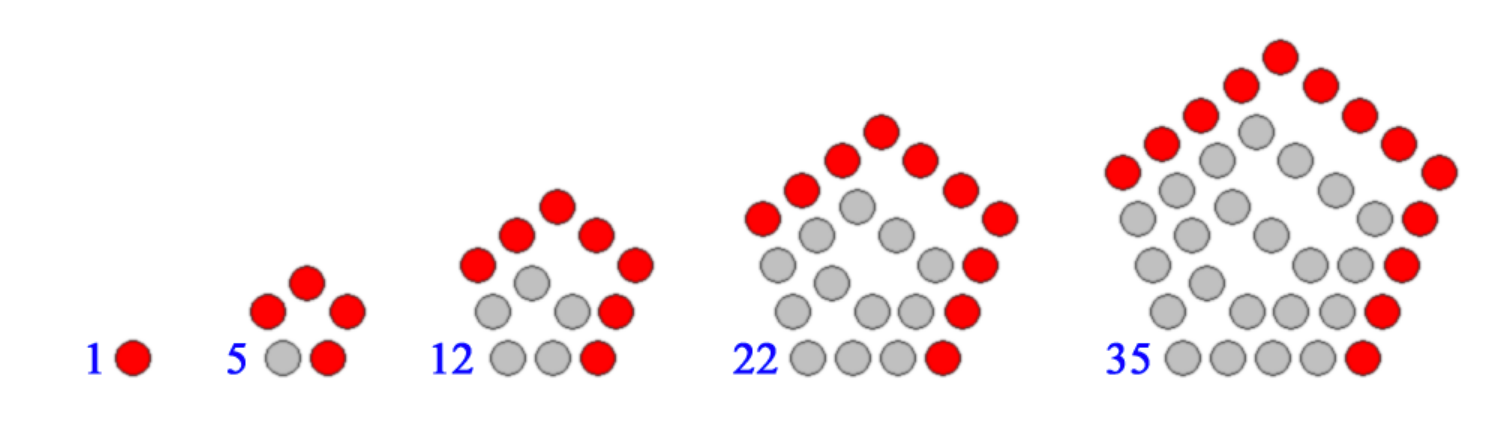
Pentagonal Numbers

You can also form a number pattern by counting the dots used to form pentagons of progressively bigger sizes as shown in the picture below:

Cube Numbers

The numbers

form a number pattern that is made up of the cubes of the counting numbers. For example, \(1 = 1 \times 1 \times 1\), \(8 = 2 \times 2 \times 2\) and \(27 = 3 \times 3 \times 3\). The next number in the pattern is found by cubing the next counting number: \(7^3 = 343\).

Fibonacci Numbers

Conclusion

There are all sorts of different number patterns. Why not see if you can come up with some of your own?