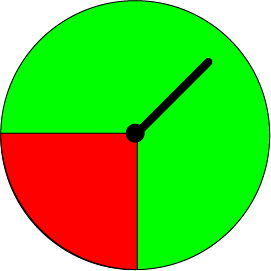
Gus isn't convinced he should paint himself green. He has a niggling feeling that red might be a better colour for him. To keep him happy, Christo designs another spinner that will make it likely that he will choose green, and unlikely (but still possible) that he will choose red. It might look something like the one in the picture. Do you see how most of the spinner is green, but just a small part (in this case \(\dfrac{1}{4}\)) is red? The arrow is much more likely to land on part of the spinner coloured green than it is to land on part coloured red.

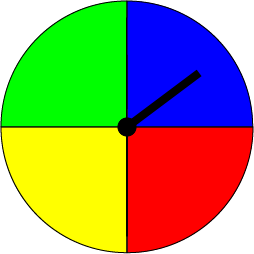
Now Gus' friend Gloria has suggested he should paint his shell pink. Christo really hates pink, so he designs a spinner with no pink on it at all. It's now impossible for Gus to spin up the colour pink. Instead, this spinner makes it equally likely for Gus to spin up blue, green, yellow or red. The parts of the spinner painted in these colours have the same size, so it's equally likely for the spinner's needle to land on each of them.

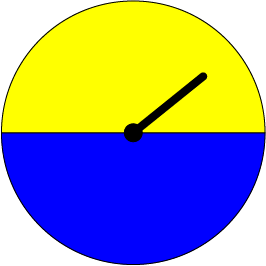
Gus has finally narrowed it down to two colours. He will either stick with his yellow shell or paint it blue. Although he's disappointed about the green, Christo designs yet another spinner. This time half of it is yellow, and the other half is blue. Both colours cover the same amount of the spinner. So, there's a 50-50 chance that, when Gus spins this spinner, it'll land on yellow, and a 50-50 chance that the arrow will land on blue.

Well, what do you think of Gus' new look? Can you guess which colour that last spinner landed on?