Decimal Numbers

Decimal numbers are numbers made out of the ten digits \(0,1,2,3,4,5,6,7,8,9\) that also contain a decimal point

This is Blublubox, a friendly alien from the planet BleBeep who is visiting the Earth. Blublubox is interested in hearing about our number system. His planet uses a number system with only six digits because his people only have six fingers, so it's quite different from our own. He really wants to hear what we do with parts of numbers.

Let's start by showing Blublubox an example.

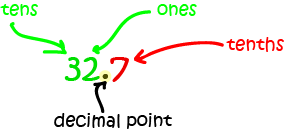
Blublubox, this is the number "thirty-two and seven tenths", written as a decimal number. Do you notice that we have tens, ones, and tenths places? The tenths are numbers smaller than a whole number, and we put a dot, called a decimal point in between the ones place and the tenths place.

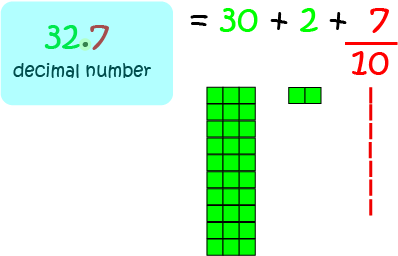
Place Value

We always know what number a numeral represents because our decimal number system uses place value. Each column of a number stands for a power of \(10\). The position of a digit in a numeral is very important.

In the number, 758:

• The "8" is in the ones column, so it stands for 8 ones (or 8)
• The "5" is in the tens column, so it stands for 5 tens (or 50)
• The "7" is in the hundreds column, so it stands for 7 hundreds (or 700)

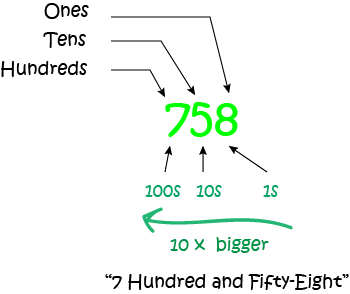
Do you notice, Blublubox, that as we move to the left, each place stands for a number that is ten times bigger? The opposite happens as we move to the left: each position stands for a value that is ten times smaller.

• Hundreds are ten times bigger than tens, which are ten times bigger than ones.
• Ones are ten times smaller than tens, which are ten times smaller than hundreds.

We use decimal numbers to write down numbers with fractional parts (parts smaller than a whole number). To do this, we need to continue our decimal number to the right, but we have to put in a decimal point first so that we can separate the whole number part and the fractional part, and so that we know exactly where the ones column is. Here's an example:

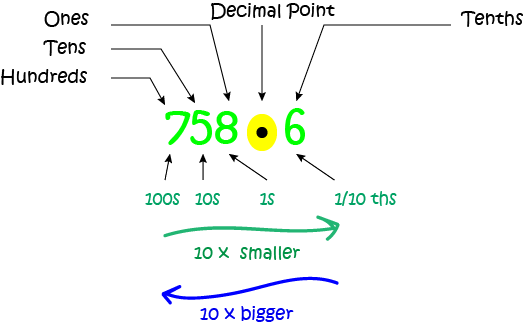
This number is seven hundred and fifty-eight and six tenths. The first column after the decimal point is the tenths column. Note that \(\dfrac{1}{10}\) is 10 times smaller than 1. We usually say this decimal number as "seven hundred and fifty-eight point six".

Of course, we can continue on to the right, making columns that stand for smaller and smaller values for as long as we like. We can include tenths, hundredths, thousandths, ten thousandths and so on. Each column is ten times smaller than the column immediately to the left of it. Here's an example:

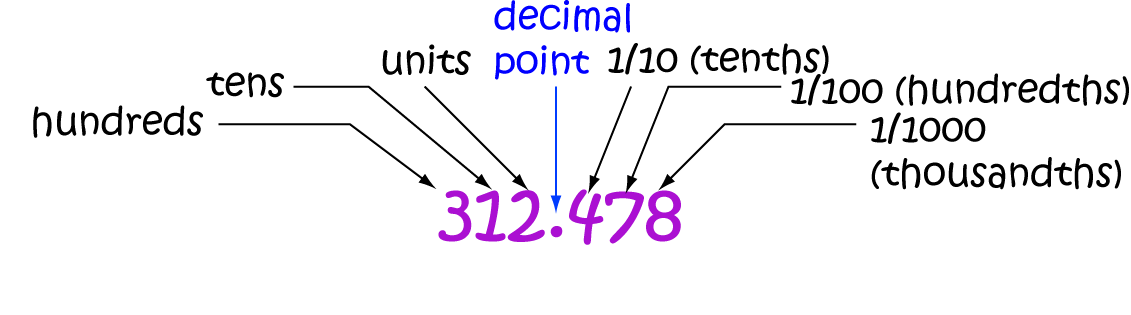
Decimal Numbers can be Very Large or Very Small

The decimal number system we use here on Earth lets us write numbers that are as large or as small as we like, Blublubox. To make a bigger number, we simply add more columns on the left. Each column is ten times bigger than the column immediately to its right. To make a smaller number, we add more columns after the decimal point. Each column is ten times smaller than the column immediately to its left.

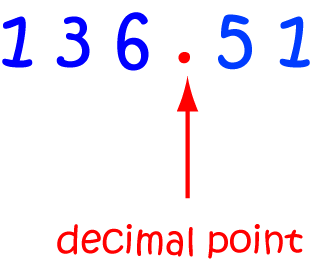
Blublubox, when we write down a decimal number, we really mustn't forget the decimal point. It is very important as it tells us exactly where the ones digit is (immediately to its left). If we don't have a decimal point, we just have to assume that we are dealing with a whole number. Sometimes people use the word "decimal number" to refer to any number in our number system, but we usually use it to mean a number with a decimal point in it.

Remember: the first digit on the left of the decimal point is the ones digit. The first digit on the right of the decimal point is the \(\dfrac{1}{10}\)ths digit.

Different Ways to Think of Decimal Numbers

Different people have different ways of thinking about decimal numbers including:

1. As a whole number plus a fraction:
   For example, you can think of the decimal number \(3.4\) as the whole number \(3\) plus \(4\) tenths, because the \(4\) is in the tenths position. So, \(3.4\) can be thought of as \(3\) and \(4\) tenths. You can think of \(23.573\) as \(23\) plus \(\dfrac{5}{10}\), plus \(\dfrac{7}{100}\), plus \(\dfrac{3}{1000}\).
2. As a decimal fraction. A decimal fraction is a fraction whose denominator (the bottom number) is a power of ten like 10,100,1000, etc. So, we can think of \(3.4\) as \(\dfrac{34}{10}\), and \(23.573\) as \(\dfrac{23573}{1000}\).
3. As a whole number with a fractional part that is a decimal fraction. For example, we can think of \(3.4\) as \(3 \; \dfrac{4}{10}\) and \(23.573\) as \(23 \; \dfrac{573}{1000}\).

So, Blublubox, there are at least three different ways that people can think of decimal numbers. All of them are equally good. It just depends on what makes the most sense to you.