Prekinder to Grade 2 Mathematics
Reflection
Reflection
Grant the Galah has noticed another galah in the water. It seems to be the same size as him, and it moves when he moves. Grant is testing it out. Yes, it looks up when he looks up, it sways to the side when he sways to the side, it lifts a claw when he lifts a claw, and it bobs up and down when he bobs up and down. Grant wonders, "How did that galah get into the water, and why is it copying me?"
You and I both know, of course, that Grant is looking at his reflection in the water. We see reflections all around us: in the mirror, in water, in the windows when its dark outside, and even in the toaster. Let's talk a bit more about reflections and the ways they are made. Photographers and painters love to use reflections in their pictures. We'll talk a little bit about how you can draw your own reflections.

The best reflections in water occur when the surface of the water is smooth, like in the picture below:

Do you notice the line running from left to right across the picture (I've drawn it in red)? It divides the picture into two halves that are copies of each other. Every point
of the picture above the red line has a copy exactly the same distance below the red line. We call the red line the mirror line, or if you want to sound very clever,
the axis of reflection. The reflection has the same size as the original object because every point of the reflection is the same distance away from the mirror line as it is in the original
object. You can see this more clearly in the picture below:
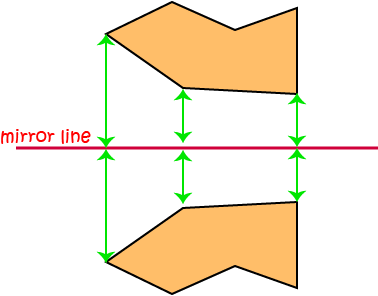
Of course, mirror lines don't have to be horizontal (run from left to right). They can run in any direction you like. Grant's mirror line goes at a bit of a slant,
and when you look in the mirror in the bathroom, your mirror line is vertical (runs up and down). The idea behind a reflection is exactly the same in all cases:
the copy of each point is exactly the same distance away from the mirror line as it was in the original object.
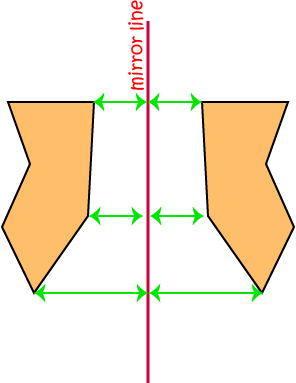
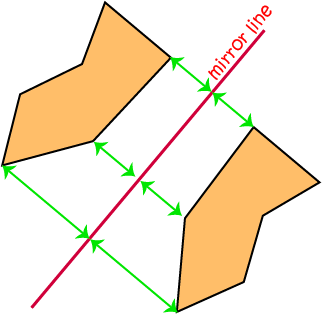
Another term for a reflection is a flip over a line.
Drawing Your Own Reflections
It's quite easy to draw your own reflections of geometric shapes. Why not try a few for yourself? You just have to complete three steps:
1. Measure the distance from each corner of the shape to the mirror line. Your distance has to be at right angles to the mirror line.
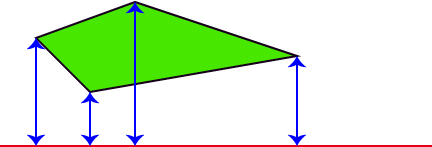
2. On the other side of the mirror line, measure the same distances at right angles to the mirror line and place a dot for each point.
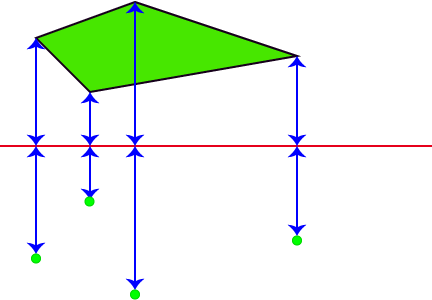
3. Join the dots and colour in the picture.
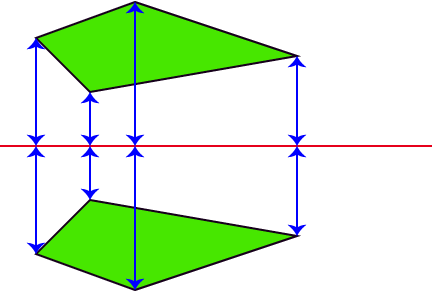
For more complicated pictures, you can just fold your paper in half, and then use a light box, or hold it up to a window, to trace the picture.
More Advanced Geometry
If you haven't heard of plotting points in the \(xy\)-plane, just ignore this for now, and come back to it when you have.
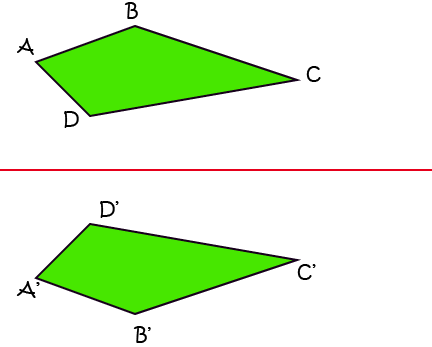
Mathematicians like to label their geometric shapes with one letter for each corner. They like to label the reflections of geometric shapes as well. It is usual to label the original point with a letter like \(A\) and its reflection with that letter, followed by a dash, like \(A'\). I've done this for the quadrilateral in the picture below. The original corners (or vertices) are labelled with \(A, B, C \) and \(D\). The corners of the reflection are labelled with \(A',B',C'\) and \(D'\). This time, I've used a horizontal mirror line.
Tricks for Horizontal and Vertical Reflection
If you need to reflect a geometric shape in the \(x\) or \(y\)-axis, there's a quick way to find its corners.
If you need to reflect the object in the \(x\)-axis, you just change each point \((x,y)\) to \((x,-y)\). This point will be in the same horizontal position as the original point, and the same distance from the \(x\)-axis (our mirror line) as the original point, but on the other side of it.
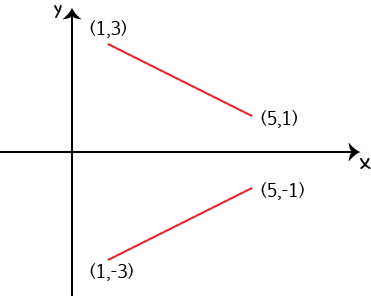
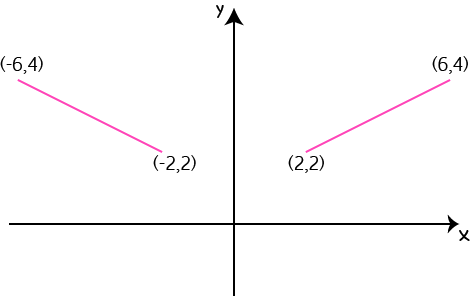
If you need to reflect the object in the \(y\)-axis, you just change each point \((x,y)\) to \((-x,y)\). This point will be in the same vertical position as the original point, and the same distance from the \(y\)-axis (our mirror line) as the original point, just on the other side of it.
So there you have it. It's quick, easy and fun to draw reflections of geometric shapes. Why don't you try a few? Maybe you could try reflecting a few different triangles and quadrilaterals. You can even make pretty patterns like this mandala using reflections, but they take a bit more effort. Have fun!

Description
This mini book covers the core of Math for Foundation, Grade 1 and Grade 2 mathematics including
- Numbers
- Addition
- Subtraction
- Division
- Algebra
- Geometry
- Data
- Estimation
- Probability/Chance
- Measurement
- Time
- Money
- and much more
This material is provided free of cost for Parent looking for some tricks for their Prekinder, Kinder, Prep, Year 1 and Year 2 children
Audience
Grade 1/Year 1, Grade 2/Year 2, Prep, Foundation, Kinder and Pre-Kinder
Learning Objectives
These lessons are for kids aged 4-8 with the core objective to expose their brains to concepts of addition, subtraction, division, algebra and much more.
Author: Subject Coach
Added on: 6th Apr 2018
You must be logged in as Student to ask a Question.
None just yet!