Reflection Symmetry

An object has reflection symmetry if one half of it can be produced by reflecting the other half. Some other terms for reflection symmetry are line symmetry and mirror symmetry.

This is Blublubox, a friendly alien who is visiting the Earth from his planet BleBeep. Everything and everyone on the planet BleBeep has reflection symmetry. If BleBeep would put his hand down, we could see that one half of Blublubox can be obtained by reflecting the other half of Blublubox in a vertical line drawn through the middle of Blublubox's head. Don't worry Blublubox, we have no intention of chopping you in half! Blublubox's line of symmetry (or mirror line) is this imaginary vertical line through the middle of the top of his head.

Blublubox was fascinated to visit the lake shown in the picture below and see this reflection. On his planet, there are only vertical lines of symmetry, but you can see a horizontal line of symmetry in this picture. It lies at the edge of the water. Sometimes reflections in water don't give perfect symmetry because the water will distort the image. This one is pretty good, however, because the water is so still and clear.

Lines of Symmetry

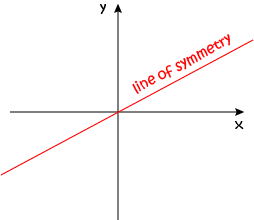
Unlike on Blublubox's planet, lines of symmetry (or mirror lines) on Earth can point in any direction. There are four directions that are most commonly used. Let's have a look at some examples of reflections in these lines of symmetry. Each of the four common lines of symmetry is named after the line it makes on the \(xy\)-plane.

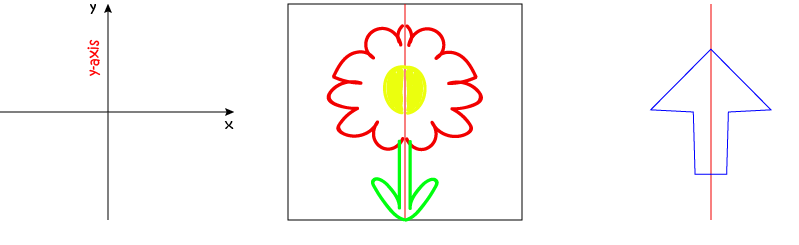
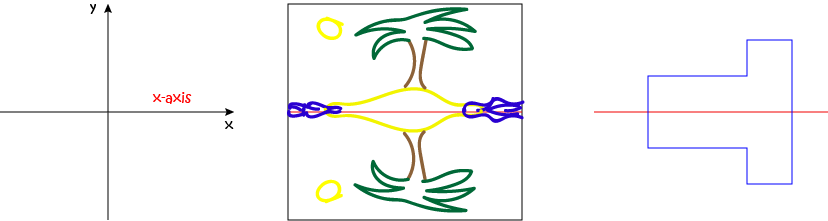
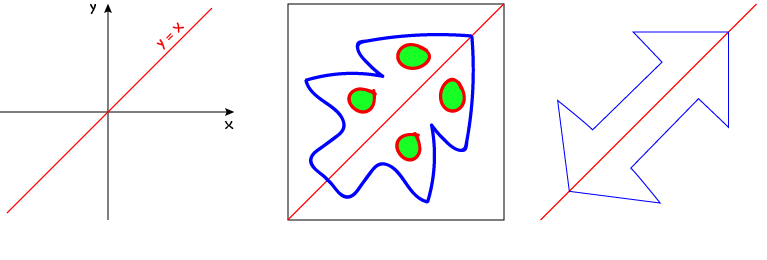
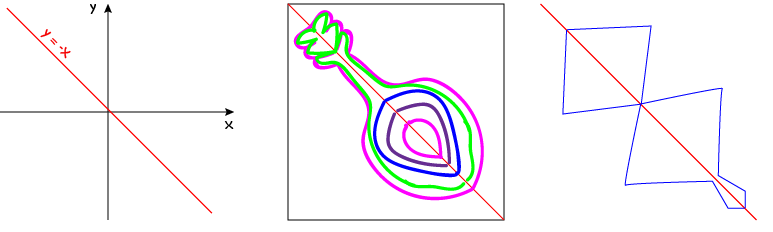
Reflection Symmetry of Plane Shapes

I think Blublubox will be very interested in this. Even plane shapes with the same number of sides can have different numbers of lines of symmetry. For example, quadrilaterals can have \(0, 1,2,3\) or \(4\) lines of symmetry as you can see in the pictures below:

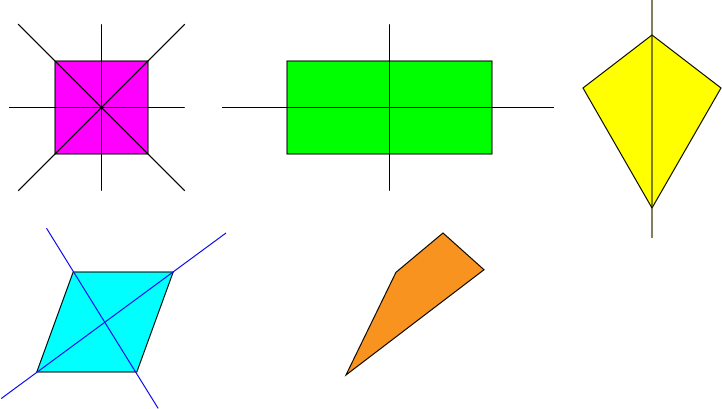
Notice how the square (top left) has 4 lines of symmetry, while the rhombus (bottom left) has only 2? The rectangle (middle top row) has 2 lines of symmetry. However, the kite (top right) has only one, vertical line of symmetry. It could have come from Blublubox's planet. Finally, at the bottom right, there is a quadrilateral with no equal sides or angles. It has no lines of symmetry.

Conclusion

There are a great many shapes that have lines of symmetry. Lines of symmetry need not be vertical, they can point in any direction.

This beautiful mandala has quite a number of lines of symmetry. Why not see if you can work out how many there are? I know Blublubox will be interested.