Tips and Tricks for Addition

Counting On (From the Larger Number)

This tip is useful when you want to add a smaller number to a larger number. Always start with the larger number first.

Let's see what you do. We'll find the answer to \(9 + 4\):

We start with the larger number, which is \(9\) and then add \(4\) to it, by moving \(4\) spaces to the right along the number line. We end up at \(13\), so \(9 + 4 = 13\).

Although you can count on from the smaller number, it's always a good idea to start with the larger number first. It doesn't matter what order you add two numbers together in, you'll always get the same answer. For example, if someone asked you to find \(3 + 8\), the easiest thing to do would be to start at \(8\) (the larger number) and count on \(3\) like this: \(8, 9, 10, 11\). If you started with \(3\), you'd have to count on \(8\), and that's a lot harder to keep track of: \(3,4,5,6,7,8,9,10,11\). In both cases you get the same answer, which is \(11\), so it's best to start with the bigger number first.

Jump Strategy

Sometimes you can make an easy jump by \(2\) or \(5\) or \(10\) to help you with the calculation.

For example, if we wanted to find \(6 + 13\), we might do a jump of \(10\) to add \(10\) to the \(6\), and then count on by \(3\) as we've done on the number line below:

We said \(6,16,17,18,19\) in our heads. So, \(6 + 13 = 19\).

Combining Numbers that Add to 10

Keep in mind that the order you add numbers in doesn't matter. Sometimes, like Patrick and his friends, we need to add up a long string of numbers. This strategy can help you out with that. Go looking for any numbers that add up to \(10\) (or \(20\) etc), and add them together first. This will simplify your addition. Let's have a look at an example:

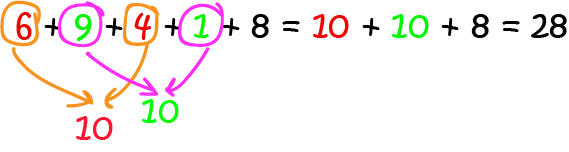
We noticed that \(6 + 4 = 10\) and \(9 + 1 = 10\), so we added these together first and changed our sum into a much easier one: \(10 + 10 + 8 = 28\). This would definitely be a good strategy for Patrick and his friends to use!

Split Strategy

In the split strategy, we use place value to split our numbers up into chunks that are easier to add. We split them up into their tens parts and ones parts (and hundreds parts if there is one). We add the parts together, and then add the two sums. Let's have a look at how we might use the split strategy to calculate \(27 + 42\):

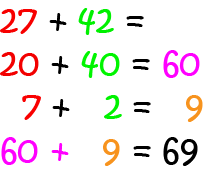
The split strategy is useful when you want to add large numbers together.

Bridging to Ten

Sometimes one of your numbers is quite close to ten. Then you can make the sum easier by borrowing enough from the second number to get up to ten, and then adding what's left over to the first \(10\). You can also bridge to \(20\) or \(30\), or even \(100\). The idea is basically the same.

Let's have a look at some examples. We'll start by working out what \(9 + 6 \) is. Now, \(9\) is very close to \(10\). We only need to add one more to get \(10\). So we steal the \(1\) from the \(6\). Now there are \(5\) left over from the \(6\). We add this \(5\) to the ten we just made to give the answer \(9 + 6 =10 + 5 = 15\). Let's see it on a number line:

In the second example, we'll bridge to \(10\) again. This time we want to find \(8 + 13\). Now, \(8\) is \(2\) away from \(10\). Let's steal those \(2\) from \(13\). This turns the sum into \(8 + 13 = (8 + 2) + (13 - 2) = 10 + 11\), which is much easier to compute. The answer is \(21\). Let's see it on the number line:

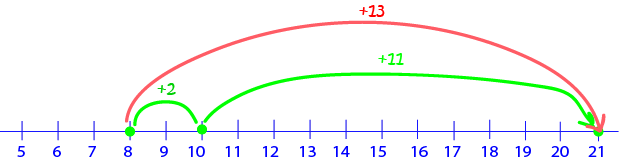
You can also bridge to \(10\) backwards. This means, you take something away from the number that is bigger than \(10\) and add it to the other number. For example, to calculate \(11 + 9\), we'd take \(1\) away from \(11\) and add it to the \(9\) to give \(11 + 9 = (11 - 1) + (9 + 1) = 10 + 10\). So, the answer is \(20\).

The Compensation Strategy

In this strategy, you add something on to a number to make a larger sum that is easier to calculate. At the end, you need to "compensate" by taking the thing you added away from your larger sum to give the correct answer.

Let's see this in action on \(7 + 9\), using a number line:

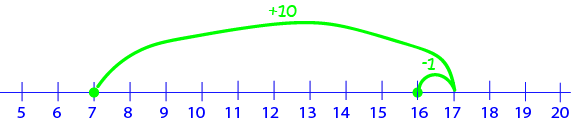
\(9\) is only \(1\) away from \(10\). It's easier to find \(7 + 10 = 17\), but that's one more than we are looking for. So, we compensate by taking away the extra \(1\) we added to give \(7 + 9 = 16\).

Let's look at another example. Suppose we were asked to calculate \(18 + 6\). Well, it's easier to add \(2\) to the \(18\) and turn the sum into \(20 + 6 = 26\). Now we have to compensate by taking our extra \(2\) away from the answer. This gives us \(18 + 6 = 26 - 2 = 24\).

How about adding some three digit numbers? Let's see if we can use this strategy on \(496 + 124\). \(496\) is four units away from \(500\), and it's easier to find \(500 + 124 = 624\). Now, compensate by taking away the extra \(4\) we added. This gives us \(496 + 124 = 624 - 4 = 620\).

Doubles and Near Doubles

If the two numbers you're adding together are the same, you can just double one of them to get your answer. For example,

What if they're only almost the same? Double the number, and then compensate if you need to. For example, if you want to find \(9 + 8\), you could think: finding \(9 + 8\) is almost like finding \(9 + 9 = 18\), but \(8\) is one smaller than \(9\), so we have to fix it up by taking one away from our answer. This gives \(9 + 8 = 18 - 1 = 17\).

Let's do one more example where we need to change both numbers. What if you need to find \(11 + 13\)? You could say, \(11\) is one less than \(12\) and \(13\) is one more than \(12\). So, we can find \(11 + 13\) by doubling \(12\) and then adding \(1\) and taking \(1\) away. But, if we add one number and then take the same number away, nothing changes. So, \(11 + 13 = 2 \times 12 = 24\).

Using Addition Tables

Using addition tables can help you with adding small numbers. You can just look the answers up! There's an article on addition tables if you'd like to learn more about this strategy.

Using Addition in Columns

This is a really handy strategy for adding larger numbers. Have a read of the article on addition in columns to find out more.