Counting Coins

Alice the cow is saving up for a new trampoline. She wants to know how much money she has already, so she's emptied out her money box and asked us to help her count the money. It looks like there's a lot of money there, Alice! I think, before we count all of this money, we'd better do a bit of practice on counting smaller amounts.

Australian Coins

Here are the different Australian coins that we'll need to count when we're helping Alice out with her money box:

Before we start counting coins, it's a good idea to sort them into groups of coins of the same value. So, we'll put all the 5 cent pieces together, all the 10 cent pieces together, and so on. Next, you should count how many of each type of coin you have, and calculate the value of each group. Finally, add the values of all the groups together. I also like to add the 1 and 2 dollar and 50 cent coins together first, and all the 5 cent, 10 cent and 20 cent coins together, before adding the whole lot together at the end. Let's try a few simpler examples to prepare us for the huge job ahead.

Example 1

Let's see if we can figure out the amount that these coins add up to:

We have 2 two dollar coins, giving four dollars, 2 one dollar coins, giving two dollars, and 4 fifty cent pieces. The total in fifty cent pieces is \(4 \times 50 = 200\) cents. Don't forget that there are \(100\) cents in a dollar, so our fifty cent pieces add up to \(200 \div 100 = \$2\). Now let's find the total: \(\$4 + \$2 + \$2 = \$8\). We've added up our first coins!

Example 2

Now we'll just add up some 5 cent, 10 cent and 20 cent pieces. We've grouped them into their types as shown in the picture below.

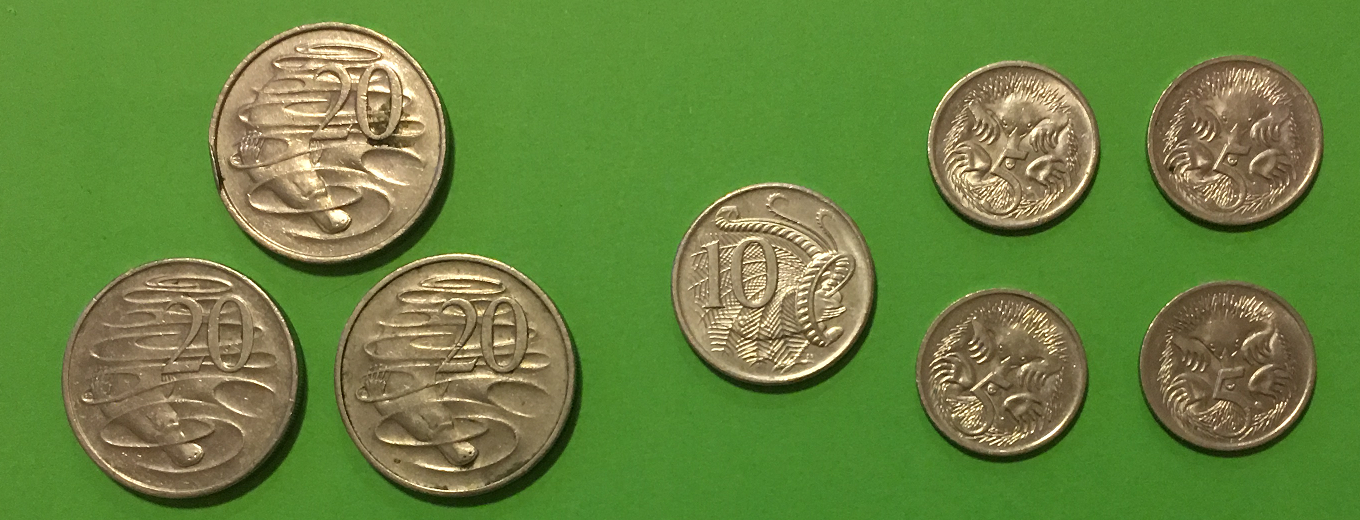
We have 3 twenty cent pieces, giving a total of 60 cents; 1 ten cent piece, for a total of 10 cents and 4 five cent pieces, giving a total of \(4 \times 5 = 20\) cents. All together, that's \(60 + 10 + 20 = 90\) cents.

Example 3

Let's try one with a fifty cent piece as well. Again, the coins have been placed in groups as shown in the picture below:

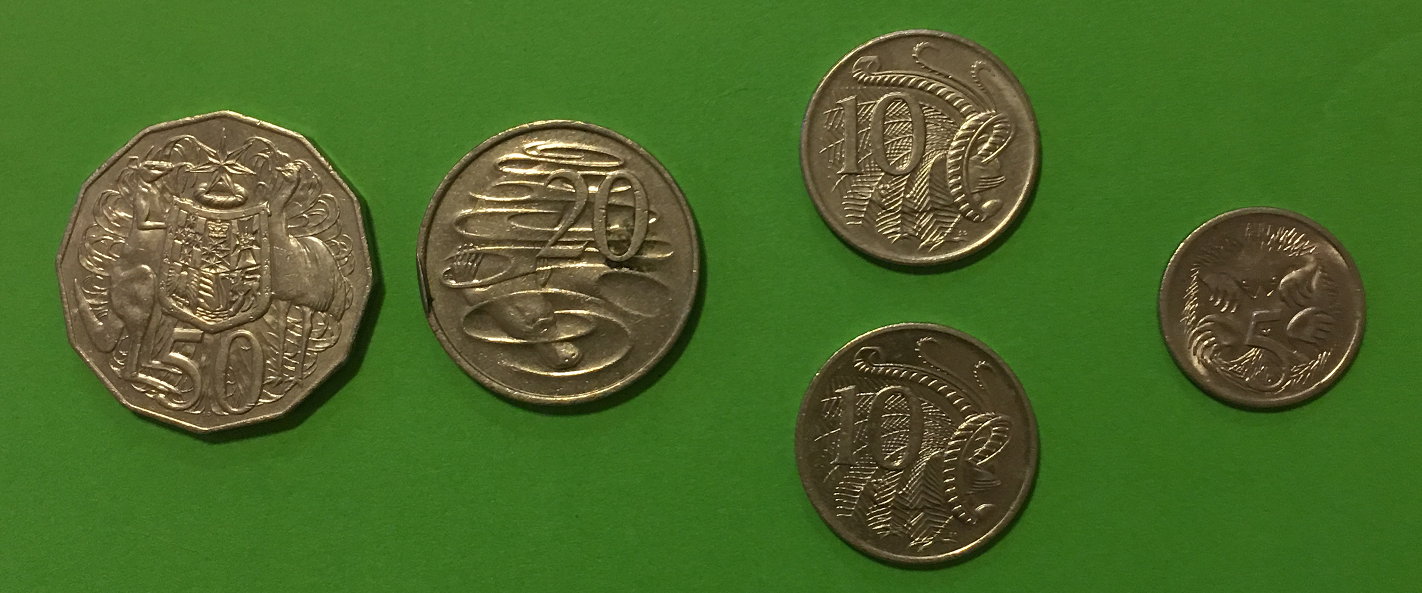
There is 1 fifty cent piece (50 cents), 1 twenty cent piece (20 cents), 2 ten cent pieces (\(2 \times 10 = 20\) cents), and 1 five cent piece (5 cents). All together, we have \(50 + 20 + 20 + 5 = 95\) cents.

Example 4

Now let's start mixing up the smaller and larger coins. In this example, there's one of each coin:

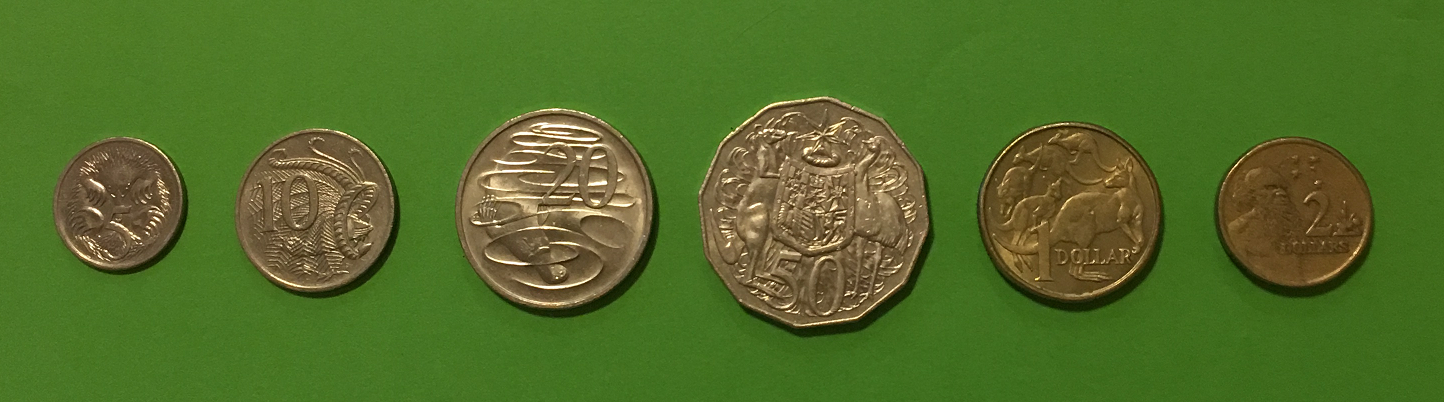
Adding the whole dollars up first gives \(\$2 + \$1 = \$3\). Now, adding the smaller coins gives \(50 + 20 + 10 + 5 = 85\) cents. So, all together, there's \(\$3 + \$0.85 = \$3.85\) in coins here.

Example 5

Let's try one last example before we move on to Alice's money box. Again, we have a mix of larger and smaller coins. We group them into their types first:

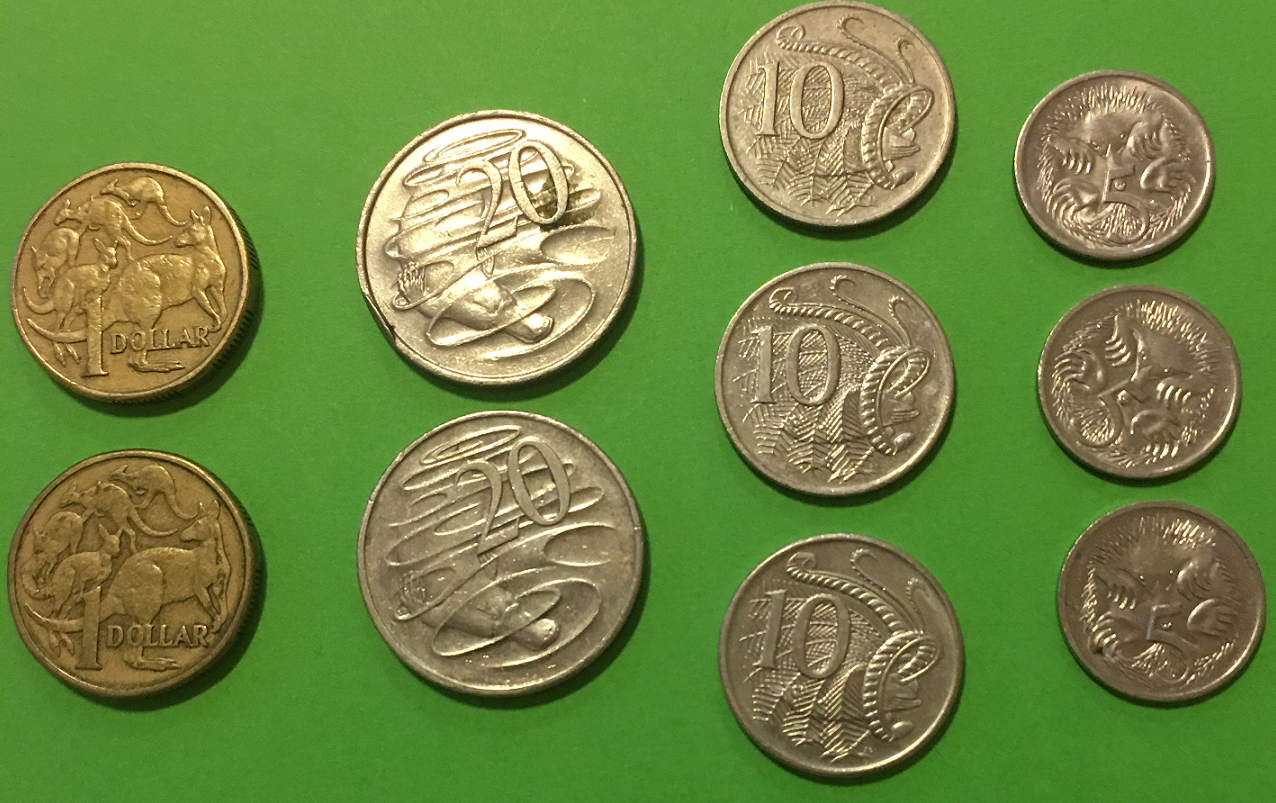
We have two \($1\) coins (adding to \(\$2\)), two 20 cent coins (adding to \(2 \times 20 = 40\) cents), three 10 cent coins (adding to \(3 \times 10 = 30\) cents), and three 5 cent coins (adding to \(3 \times 5 = 15 \) cents). This gives a total of \(\$2\) plus \(40 + 30 + 15 = 85\) cents. So, all together, we have \($2.85\) in this example.

Time to Help Alice

Yes, Alice, I know you are getting impatient, but we are ready to help you now. This could take a while... you have a lot of coins there. I think the best approach is to use a table. Sort the coins into each type. Within the types, stack them up into groups of ten, then count away as you fill in the table. Here's my table:

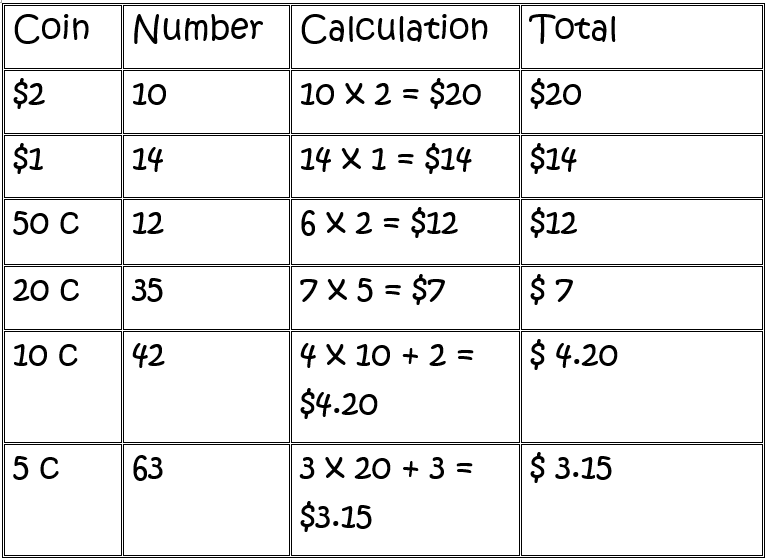
Alice has ten \(\$2\) coins, for a total of \(\$20\). There are \(14\) one dollar coins for a total of \(\$14\). She has \(12\) fifty cent pieces. Two \(50\) cent pieces make a dollar, so there are \(\$6\) in fifty cent pieces. Now let's look at the \(20\) cent coins. Alice has \(35\) of those. There are \(5\) twenty cent coins in \(\$1\), so Alice has a total of \(\$7\) in \(20\) cent pieces. She also has \(42\) ten cent pieces. Ten ten cent pieces make one dollar, so this comes to \(\$4.20\). Finally, she has \(63\) five cent pieces. There are \(20\) five cent pieces in \(\$1\), so this gives us \(\$3.15\).

Now we've added up all of Alice's groups, it's time to work out how much she has all together. The total is \(\$20 + \$14 + \$12 + \$7 + \$4.20 + \$3.15 = \$ 60.35\).

That's not quite enough for a new trampoline, Alice, but it's a really good start!

Conclusion

It was fun helping Alice with her money box, wasn't it? It's a great idea to get used to counting coins. Maybe you could count the coins in your own money box. Why not have a look around your house and see if you can find some coins to count? A good place to look is under the cushions on the lounge. Make sure you ask someone first, though. They probably won't mind if you tell them you're practising your maths, and, you never know, they might even let you keep the coins afterwards.