Fixing Equations

Sometimes we have an equation that is missing a value, and we need to work out what value to put into the equation to make it true. Alice the cow has an equation like this.

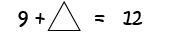
Techniques for Fixing Addition Equations

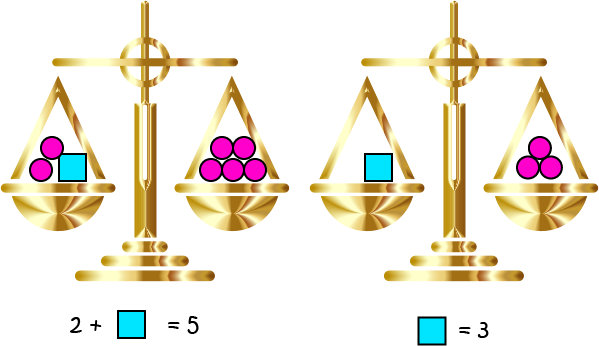
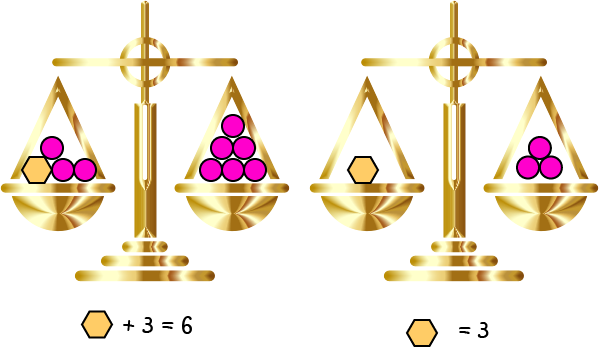
1. Using Balance Scales

Example 1

Let's see if we can fix the equation

using balance scales. Start by drawing a balanced scale with two pink balls and four green balls in one pan, and the yellow triangle in the other pan (one ball for each number in the equation). Count up the number of balls in the first pan: there are \(6\). For the bar on the scales to be level, the triangle must weigh the same as six balls. We can fix our equation by replacing the triangle by \(6\).

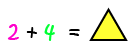
Example 2

Let's see if we can fix the equation

using balance scales. Start by drawing a balanced scale with two balls and a box in one pan, and five balls in the other (one ball for each number in the equation). Remove two balls from each pan, as shown in the picture below: The scales should still be balanced because we've taken the same amount out of each pan. Now all that is left is the box in one pan, and three balls in the other pan. As the bar of the scale is perfectly level, the box must weigh the same as the three balls. So, to fix the equation, we have to replace the box by \(3\).

Example 3

Let's see if we can fix the equation

using balance scales. Start by drawing a balanced scale with three balls and the hexagon in one pan, and six balls in the other (one ball for each number in the equation). Remove three balls from each pan, as shown in the picture below: The scales should still be balanced because we've taken the same amount out of each pan. Now all that is left is the hexagon in one pan, and three balls in the other pan. As the bar of the scale is perfectly level, the hexagon must weigh the same as the three balls. So, to fix the equation, we have to replace the hexagon by \(3\).

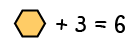
2. Using Number Lines

You can also fix addition equations using number lines. Let's have a look at a few examples.

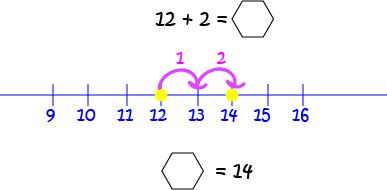
Example 4

In this example, we just need to do a straight out addition of \(12\) and \(2\) as the two numbers are on the left hand side of the equation.

Put a dot down at \(12\) and count two spaces to the right. You'll end up at \(14\). So, to fix this equation, we need to replace the hexagon by \(14\).

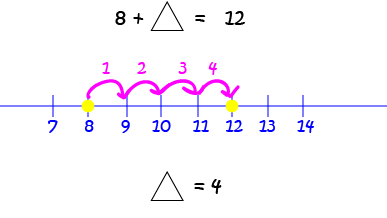
Example 5

In this example, we need to find something to add to \(8\) that will give us \(12\). Let's have a look at the number line:

We put circles on the number line at \(8\) and \(12\) and worked out how many spaces we had to jump over to get from \(8\) to \(12\). We need to skip over \(4\) spaces, so we had to add \(4\) to \(8\) to give \(12\). To fix this equation, we need to replace the triangle by \(4\).

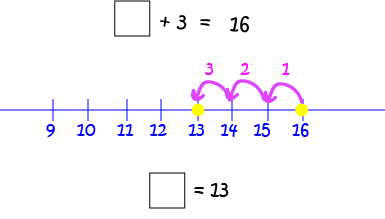
Example 6

In this example, we need to find something to add to \(3\) that will give us \(16\). We could put down dots at \(3\) and \(16\) and count the number of spaces between them, but this would take a long time. Instead, let's start at \(16\) and count back \(3\). Let's see this on the number line:

We end up at \(13\). So, we need to add \(13\) to our \(3\) to get sixteen. To fix this equation, we need to replace the box by \(13\).

3. Using Doubles and Near Doubles

Sometimes you can fix an equation using doubles or near doubles. Let's have a look at a few examples.

Example 7

Let's fix the following equation:

We need to find something to add to \(2\) to give \(4\). But, \(4\) is just double \(2\), so we can replace the box by \(2\) and fix the equation.

Example 8

How about this equation?

We need to find something to add to \(3\) to give \(7\). This time \(7\) isn't double \(3\), but it's pretty close. If we add \(3\) to \(3\), we get \(6\). We need to add one more to get \(7\). So, we can fix this equation by replacing the pentagon by \(4\).

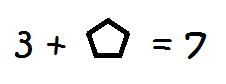
Fixing Other Equations

We can also fix subtraction and multiplication equations. Let's look at a few examples.

Fixing Subtraction

As subtraction is just the reverse of addition, we can use the same techniques to fix subtraction equations. Let's try a couple using the number line.

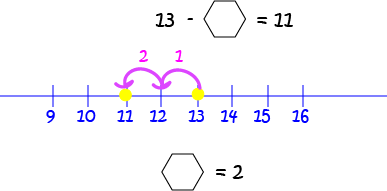
Example 9

In this equation, we need to find a number that you can subtract from \(13\) to give \(11\).

We put dots down at \(13\) and \(11\), and count up the number of spaces we need to skip over backwards to reach \(11\) from \(13\) (or forwards to reach \(13\) from \(11\)). In either case, we skip over two spaces, so we need to replace our hexagon by \(2\) to fix this equation.

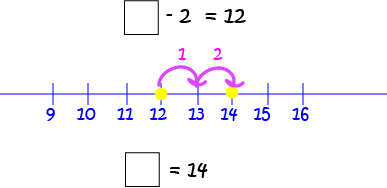
Example 10

In this equation, we need to find a number that you can subtract \(2\) from to give \(12\).

We put a dot down at \(12\) and skip over \(2\) spaces to the right to land on \(14\). You can check this one by starting at \(14\) and moving two spaces to the left to subtract \(2\). You end up at \(12\). So, to fix this equation, we need to replace the square by \(14\).

Fixing Multiplication Equations

To fix multiplication equations, we can use skip counting. Let's have a look at an example.

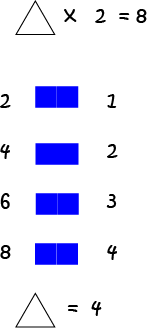
Example 11

In this example, we need to find a number that we can multiply by \(2\) to give \(8\). This is the same as finding a number we can multiply \(2\) by to give \(8\). Start at \(2\) and skip count by twos until you reach \(8\). Keep count of how many numbers you say as you go. This will give you the answer:

We said \(4\) numbers while skip counting from \(2\) up to \(8\), so we can fix this equation by replacing the triangle by \(4\).

Fixing Alice's Equation

Now we can solve Alice's problem. Remember that she needed to work out how many extra barrels she needed to build her raft? We'll use a number line to fix Alice's equation:

We need to skip over three spaces to get from \(9\) to \(12\), so to fix Alice's equation, we need to replace the triangle by \(3\). In other words, Alice needs three more barrels to build her raft.

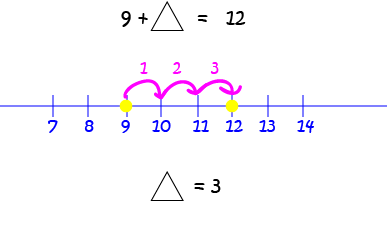
Have fun shooting those rapids, Alice! Don't forget to wear a helmet.