Prekinder to Grade 2 Mathematics
Addition Tables
Addition Tables

Cuthbert the crab has decided to teach his friend Clarissa how to do addition. A good way to start out when you're learning addition is to use an addition table like the one shown below. That way, you can practise doing lots of addition sums and you'll start to memorise the correct answers to the ones that you do most commonly. It's a great idea to be able to remember all the possible totals you get by adding the numbers from one to ten. This is exactly what Cuthbert has decided to help Clarissa with.

This is an addition table for the numbers from \(1\) to \(10\):
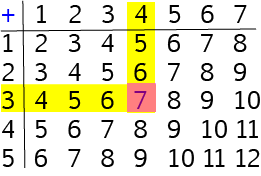
Cuthbert and Clarissa use an addition table like this one, but a bit bigger so that they can crawl along the columns and rows of their table to find the right answer. For example, to add \(2\) and \(3\), Cuthbert will crawl along the row beginning with \(2\) and Clarissa will crawl down the column labelled \(3\). The place where they bump into each other will be the square containing their answer, which is \(5\).
You probably won't be able to crawl around on an addition table like Cuthbert and Clarissa, but you will be able to use your fingers to do the same job. Let's have a look at a few examples.
Let's start by using our addition table to add the numbers \(3\) and \(4\). Place one finger on the row labelled \(3\) and another finger (use your other hand!) on the column labelled \(4\). Now run your fingers across the row and down the column until they meet. The square where they meet will be the answer. It's shown by the orangey-red square in the diagram: \(4 + 3 = 7\).
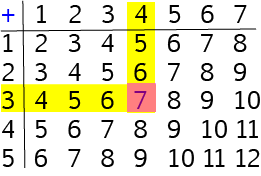
As I'm sure you'll remember, it doesn't matter which order we add numbers together in. You will also get the same answer if you place one finger on the row labelled \(4\) and another finger on the column labelled \(3\). If you run your fingers across the row and down the column, they will meet at the square containing the answer. This is the orangey-red square in the diagram: \(3 + 4 = 7\).
Let's try a couple more examples.
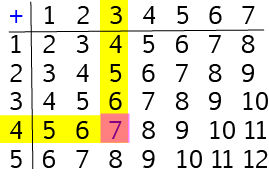
Let's use our addition table to add the numbers \(4\) and \(7\). Place one finger on the row labelled \(4\) and another finger (use your other hand!) on the column labelled \(7\). Now run your fingers across the row and down the column until they meet. The square where they meet will be the answer. It's shown by the orangey-red square in the diagram: \(4 + 7 = 11\).

As I'm sure you'll remember, it doesn't matter which order we add numbers together in. You will also get the same answer if you place one finger on the row labelled \(7\) and another finger on the column labelled \(4\). If you run your fingers across the row and down the column, they will meet at the square containing the answer. This is the orangey-red square in the diagram: \(7 + 4 = 11\).
And now we have time for one last example.
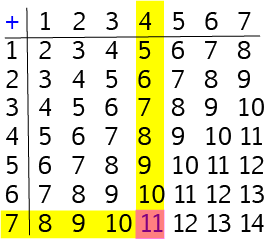
Let's use our addition table to add the numbers \(8\) and \(9\). Place one finger on the row labelled \(8\) and another finger (use your other hand!) on the column labelled \(8\). Now run your fingers across the row and down the column until they meet. The square where they meet will be the answer. It's shown by the orange square in the diagram: \(8 + 9 = 17\).

As I'm sure you'll remember, it doesn't matter which order we add numbers together in. You will also get the same answer if you place one finger on the row labelled \(9\) and another finger on the column labelled \(8\). If you run your fingers across the row and down the column, they will meet at the square containing the answer. This is the orangey-red square in the diagram: \(9 + 8 = 11\).

Conclusion
It's a good idea to practise your addition using tables like Cuthbert and Clarissa. After a while, see if you can think of the answer before you use the table. Just use the table to check if you're right. It won't be long before you've memorised the sums of all the pairs of numbers between one and ten.
If you want to add bigger numbers, addition tables won't really help you because they just get too big and difficult to handle. Don't worry though, there are plenty of other methods we can use for adding larger numbers. Having memorised the sums of pairs of numbers between one and ten will really help you out when you try to add larger numbers.
Description
This mini book covers the core of Math for Foundation, Grade 1 and Grade 2 mathematics including
- Numbers
- Addition
- Subtraction
- Division
- Algebra
- Geometry
- Data
- Estimation
- Probability/Chance
- Measurement
- Time
- Money
- and much more
This material is provided free of cost for Parent looking for some tricks for their Prekinder, Kinder, Prep, Year 1 and Year 2 children
Audience
Grade 1/Year 1, Grade 2/Year 2, Prep, Foundation, Kinder and Pre-Kinder
Learning Objectives
These lessons are for kids aged 4-8 with the core objective to expose their brains to concepts of addition, subtraction, division, algebra and much more.
Author: Subject Coach
Added on: 6th Apr 2018
You must be logged in as Student to ask a Question.
None just yet!