What does it mean for a function to be differentiable?

A differentiable function is one you can differentiate.... everywhere!

That sounds a bit like a dictionary definition, doesn't it? Completely accurate, but not very helpful! But, if you explore this idea a little further, you'll find that it tells you exactly what "differentiable means".

Differentiable functions are nice, smooth curvy animals. They have no gaps or pointy bits.

Example

Is the function \(f(x) = x^3 + 3x^2 + 2x\) differentiable?

The rules of differentiation tell us that the derivative of \(x^3\) is \(3x^2\), the derivative of \(x^2\) is \(2x\), and the derivative of \(x\) is \(1\). So, the derivative of \(f\) is \(f'(x) = 3x^2 + 6x + 2\).

This derivative exists for every possible value of \(x\)! So, \(f\) is differentiable: we can find it's derivative everywhere!

Making the definition more precise (a.k.a. keeping the mathematicians happy)

Most of the above definition is perfectly acceptable. The only thing we really need to nail down is what we mean by "everywhere". Does this mean that we take the function on a trip, and try to differentiate it at every place we visit? Of course not! What we mean is that we can evaluate its derivative at every value of \(x\) that we can input into the function definition. There's a technical term for these \(x\)-values:

Domain of a function

The domain of a function is the set of allowable \(x\)-values (or input values) for the function. Sometimes, the domain of the function is explicitly stated. Other times, we have to work it out from what the function definition will allow. In these cases, the domain will be the largest set of \(x\)-values that can be sensibly input into the function definition. For example, the function \(f(x)= \dfrac{1}{x}\) only makes sense for values of \(x\) that are not equal to zero. Its domain is the set \(\{x \in \mathbb{R}: x \neq 0\}\). In other words, it's the set of all real numbers that are not equal to zero.

So, a function is differentiable if its derivative exists for every \(x\)-value in its domain.

Example

Let's have another look at our first example: \(f(x) = x^3 + 3x^2 + 2x\).

\(f(x)\) is a polynomial, so its function definition makes sense for all real numbers. Its domain is the set of all real numbers.

We found that \(f'(x) = 3x^2 + 6x + 2\), which is also a polynomial. So the derivative of \(f(x)\) makes sense for all real numbers. \(f(x)\) can be differentiated at all \(x\)-values in its domain. Therefore, it is differentiable.

Another example:

This time, we want to look at the absolute value function, \(f(x) = |x|\). Just a quick reminder...

\( |x| = \begin{cases} x &\text{ if } x \geq 0\\ -x &\text{ if } x and this function definition makes sense for all real numbers \(x\). So, the domain is all real numbers.

The question is ... is \(f(x)\) differentiable? Can we find its derivative at every real number \(x\)? Let's start by having a look at its graph.

Notice the extremely pointy bit at \(x = 0\), where the function definition changes from \(f(x) = x\) to \(f(x) = -x\).

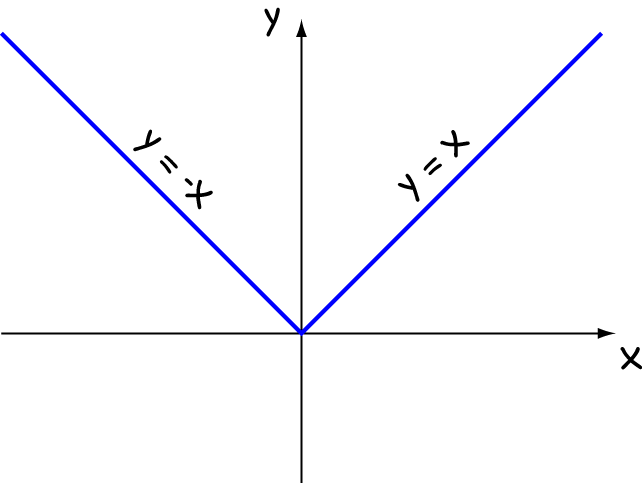
The derivative certainly exists for \(x\)-values corresponding to the straight line parts of the graph, but we'd better check what happens at \(x = 0\).

Is the derivative defined at x = 0?

Remember that the derivative is a slope? That's why I'm a bit worried about what's going on at \(x = 0\) in this function. The slope of the graph changes abruptly. We can check whether the derivative exists at any value \(x = c\) by checking whether the following limit exists:

\( \displaystyle{\lim_{h \to 0} \frac{f(c + h) - f(c) }{h}}\).

If you look at the above limit closely, you'll see that it's just the definition of the derivative at \(x = c\). So, by checking whether this limit exists, we're just checking whether the derivative is defined at \(x = c\).

Let's check what happens at \(c = 0\):

\(\begin{align*} \lim_{h \to 0} \frac{f(c + h) - f(c)}{h} &= \lim_{h \to 0} \frac{|c + h| - |c|}{h}\\ &= \lim_{h \to 0} \frac{|0 + h| - |0|}{h}\\ &= \lim_{h \to 0} \frac{|h|}{h} \end{align*}\)

But this final limit doesn't exist! If we let \(h\) approach zero from above and below, we get different answers because the function definition is different on either side of \(x = 0\):

• From the left: \(\displaystyle{\lim_{h \to 0^-} \frac{|h|}{h} = \lim_{h \to 0^-} \frac{-h}{h} = -1}\)
• From the right: \(\displaystyle{\lim_{h \to 0^+} \frac{|h|}{h} = \lim_{h \to 0^+} \frac{h}{h} = 1}\)

For the limit to exist, the limits from the left and right have to be equal, and these aren't! This tells us that we can't find the derivative of \(f(x)\) at \(x = 0\), and so \(f(x) = |x|\) is NOT differentiable.

Visualising Differentiable Functions

If you were to put a differentiable function under a microscope, and zoom in on a point, the image would look like a straight line.

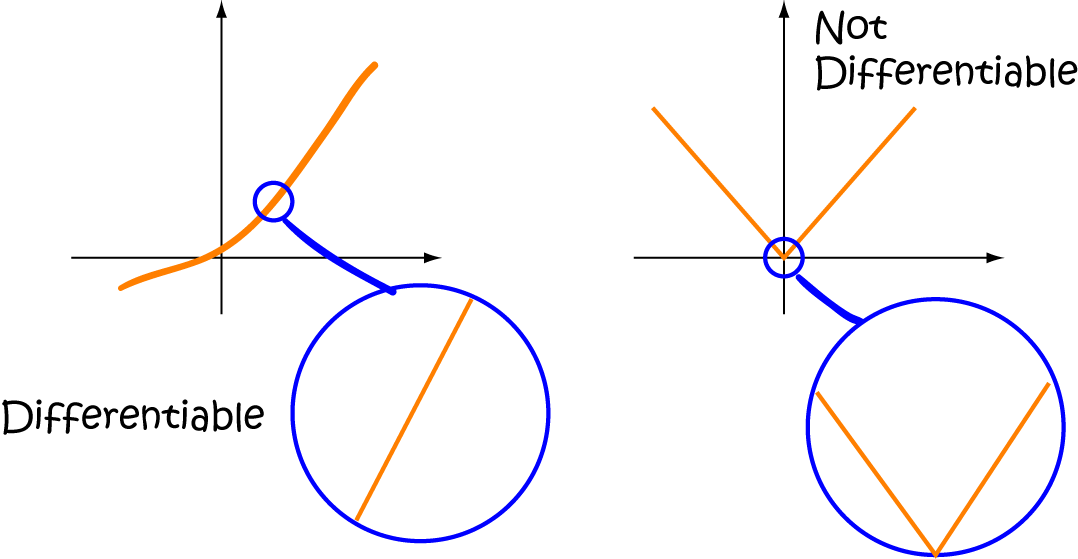
When you zoom in on the pointy part of the function on the left, it keeps looking pointy - never like a straight line. So this function is not differentiable, just like the absolute value function in our example.

Other problem children

Here are some more reasons why functions might not be differentiable:

Step functions are not differentiable. You can't find the derivative at the end-points of any of the jumps, even though the function is defined there.

The fifth root function \(x^{\frac{1}{5}}\) is not differentiable, and neither is \(x^{\frac{1}{3}}\), nor any other fractional power of \(x\). The slope is vertical at \(x = 0\), and the derivative, \(y' = \frac{1}{5}x^{-\frac{4}{5}}\) is undefined there.

Rational functions are not differentiable. They are undefined when their denominator is zero, so they can't be differentiable there. For example, we can't find the derivative of \(f(x) = \dfrac{1}{x + 1}\) at \(x = -1\) because the function is undefined there.

Functions that wobble around all over the place like \(\sin\left(\frac{1}{x}\right)\) are not differentiable. This function oscillates furiously around \(x = 0\), and its slope never heads towards any particular value. So, it can't be differentiable at \(x = 0\)!

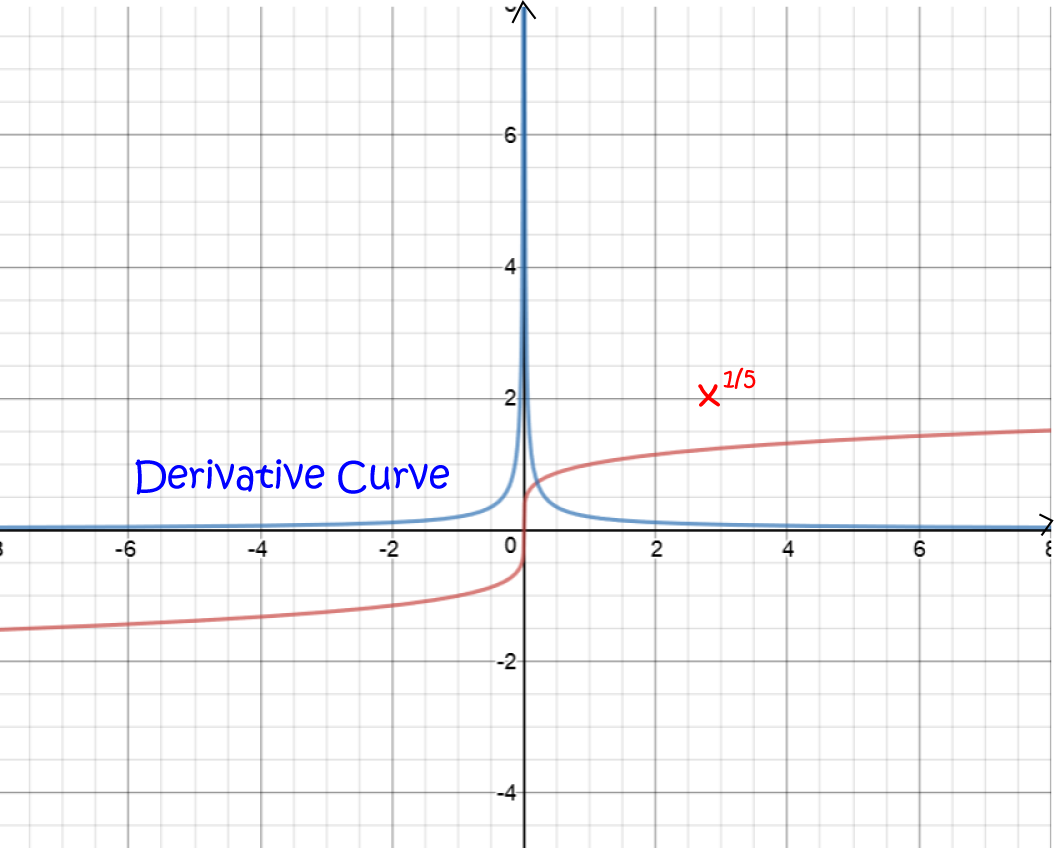
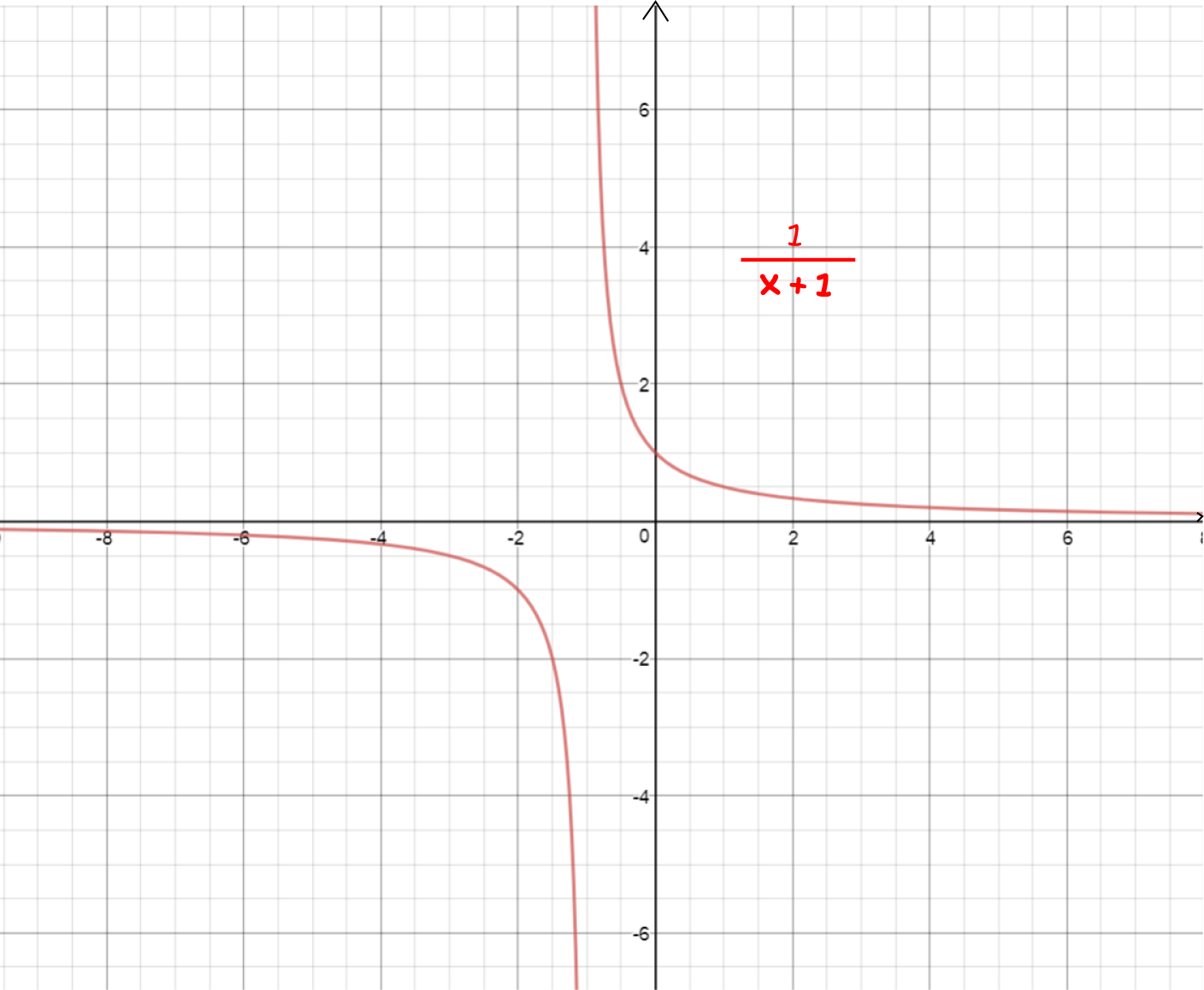
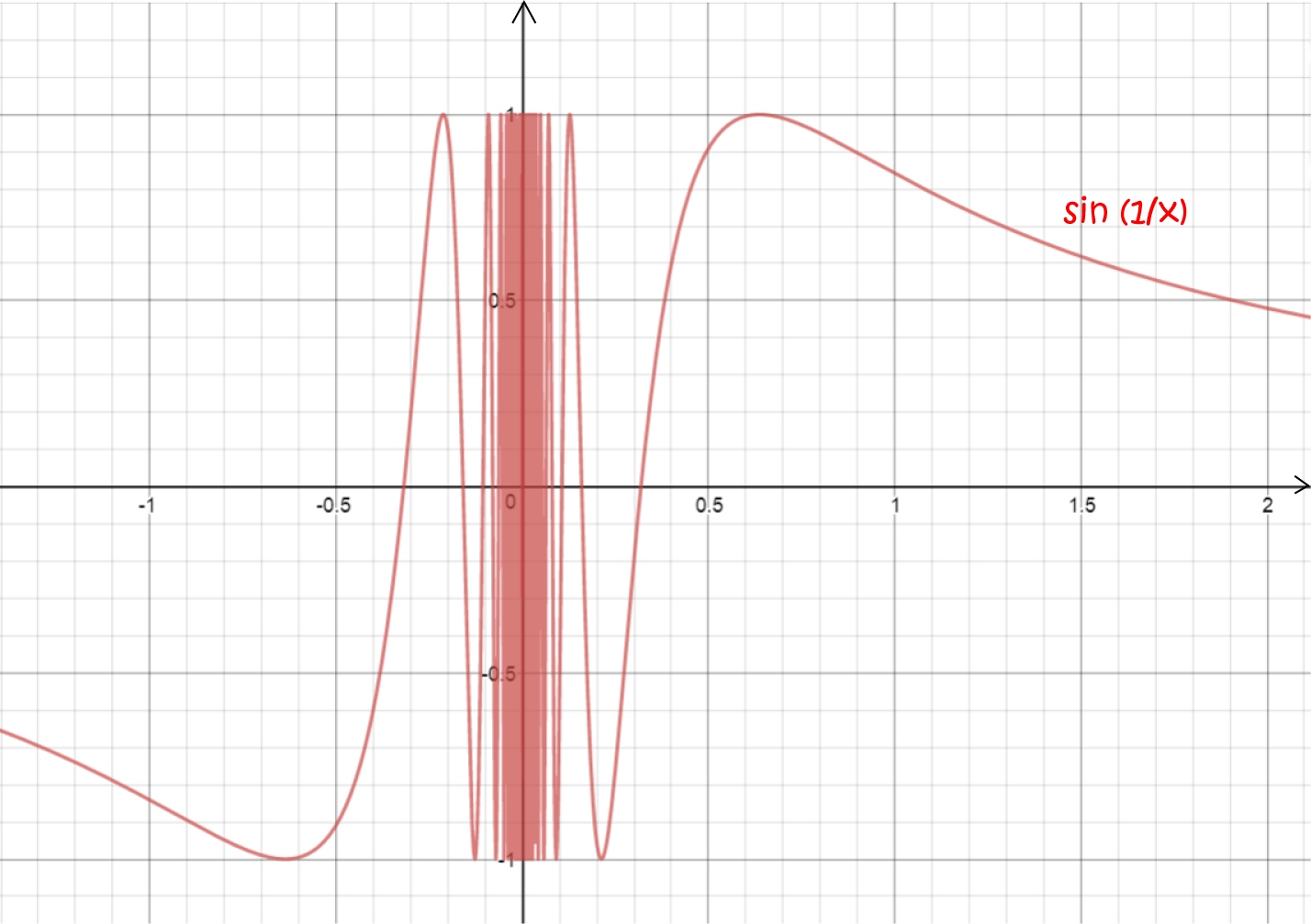
Does restricting the domain help a function to be differentiable?

It can, provided the new domain doesn't include any points where the derivative is undefined!

Example:

Is the function \(g(x) = |x|\), with domain \((0,\infty)\) differentiable? The interval \((0,\infty)\) refers to all the positive real numbers, and does NOT include zero. We know that \(g(x) = x\) on this interval, and this is definitely a differentiable function. So, the answer is 'yes!': the function \(g(x)\) is differentiable over its restricted domain.

Of course there are other ways that we could restrict the domain of the absolute value function. It will be differentiable over any restricted domain that DOES NOT include zero.

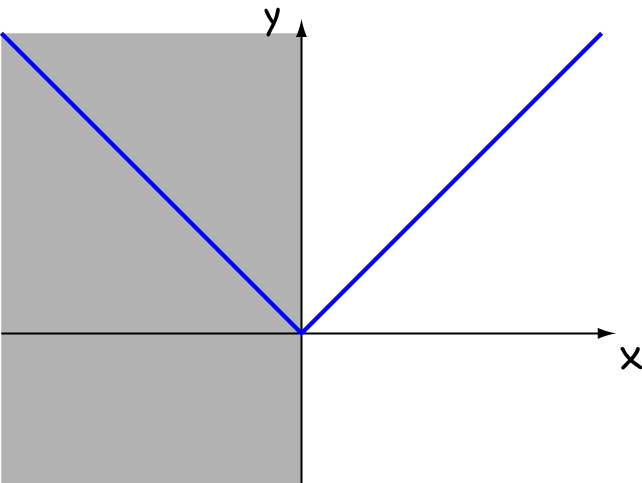
Why do we care?

We care about differentiable functions because they're the ones that let us unlock the full power of calculus, and that's a very good thing!

A remark about continuity and differentiability

If a function is differentiable, then it must be continuous. However, there are lots of continuous functions that are not differentiable. The absolute value function that we looked at in our examples is just one of many pesky functions.