The Concept of Infinity

One day, Sam, Al and Jasmin decide to find out who takes the most steps when walking home from school. Al and Sam decide to count each step they take, but Jasmin comes up with a more advanced method.

Al: I can't be bothered counting all those steps. I know it's a long way, so I'll go about half-way and then start at infinity....

...Infinity plus one, infinity plus two, infinity plus three, ...

Sam (overhearing Al talking to himself): I'm sure my house is further away than Al's. I'll go about one third of the way, and then start counting at infinity plus five...

...Infinity plus five, infinity plus six, infinity plus seven, ...

Jasmin (notices what they are doing and shakes her head): Why don't they just use the step counters on their phones? That's what I'm doing.

The next day at school, the three friends meet to compare numbers.

Jasmin (pulls out her phone): I took 3,954 steps.

Al: Is that all? I took infinity plus 1,542 steps.

Sam: I took even more! I took infinity plus 3,562 steps.

Jasmin: That's impossible! Neither of you could have taken infinity steps. Infinity isn't even a number. And... infinity plus 1,542 is just the same thing as infinity plus 3,562. They're all infinity!

Sam and Al look bewildered. Jasmin walks off shaking her head.

Things that Go On Forever

It turns out that Jasmin was right. Infinity isn't a number at all. It is just the name we give to something that is so big that it can never be reached.

Things like the counting numbers go on for ever and ever. The counting numbers are infinite:

Every time someone thinks they've come up with a really big counting number, let's call it Hugh Mungous, someone else comes along and says they've thought of a bigger one: Hugh Mungous\( + 1\).

So, there is no such thing as the biggest counting number! We express this idea by saying that there are infinitely many counting numbers, not by inventing a number called infinity. So Sam and Al couldn't possibly have taken infinity steps, could they?

Examples of Infinite Things

Let's have a look at some more examples of things that go on forever and ever. Infinite objects are very important in mathematics.

The Counting Numbers

We've already seen that the counting numbers \(\{1,2,3,\dots\}\) are infinite. Mathematicians sometimes call the counting numbers the natural numbers. However, some mathematicians (and most computer scientists) say that the natural numbers start at \(0\). The crazy thing is that the sets \(\{0,1,2,3,\dots\}\) and \(\{1,2,3,\dots\}\) have the same number of elements. They are both infinite! If you started counting from -1,542, you'd still get the same (infinite) number of counting numbers, not more. So Jasmin was right again, if infinity existed, we'd have \(\infty + 1,542 = \infty\) and \(\infty + 3,563 = \infty\). Pretty weird, huh?

Straight Lines

You've drawn straight lines in maths, haven't you? Your teacher always insists that you put arrows on both ends of them to show that the line continues on forever and ever. That's because lines are infinite: they extend without bounds in both directions.

There are other parts of lines that you'll have come up against in maths. The part of a line that starts from one point and then goes on forever in one direction is called a ray. The part of a line that has two end points is called a line segment.

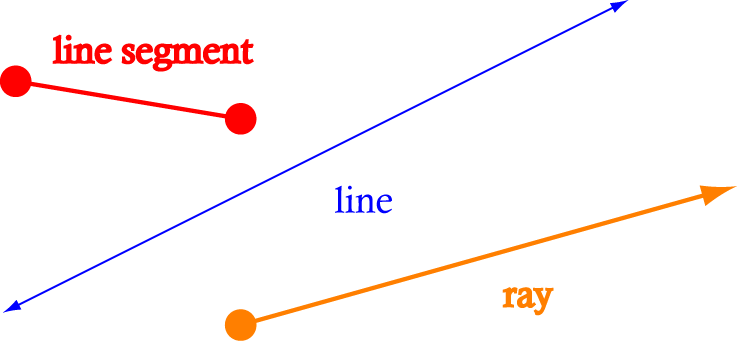
A line contains infinitely many points . So does a ray, and even a line segment.

Infinitely Many Decimal places

When you write some numbers as decimals, their decimal places go on forever and ever. For example, \(\frac{1}{3} = 0.333333333333 \dots\) has infinitely many \(3\)s after the decimal point, and \(\pi = 3.14159265359\dots\) also has an infinite number of decimal places. The difference is that \(\pi\)'s decimal places don't form any kind of pattern.

Weird number fact: You can write the number \(1\) as a decimal with infinitely many decimal places: \(1 = 0.999999999999 \dots\)

Another weird fact: Not all infinite sets have the same number of elements. There are more real numbers than natural numbers. In fact, there are more real numbers in the interval \(0 \leq x \leq 1\) than there are natural numbers. This is getting into university-level mathematics, but it definitely seems weird!

Infinite Sequences

We can find all sorts of different infinite sequences.

• The sequence \(2,4,6,8,10,\dots\) is infinite.
• So is the sequence \( \dfrac{1}{1}, \dfrac{1}{2}, \dfrac{1}{3},\dfrac{1}{4},\dots\).
• Another infinite sequence is ABAABAAABAAAAB...

Finite Things

What do we mean by finite? Well, you might say that something is finite if it isn't infinite, but that isn't very helpful.

Let's try to make the idea a bit more precise: something is finite if it doesn't go on forever and ever. In other words, an object is finite if you eventually come to a stop when you count its parts. Mathematicians still wouldn't be happy, but we're getting closer.

Let's think about what we're doing when we count something. We line up each of its parts and say "This is the first one, this is the second one,..." and so on until we reach the last part, and say "This is the nth one." We've run out of parts, so there are no more to count, and we know that our object has \(n\) parts. The parts stop! The object is finite.

So how would mathematicians say this? It would go something like this:

A set \(S\) is finite if we can find a natural number \(N\) and labelling map \(L: S \to \{1,\dots, N\}\) that labels every element of \(S\) with a different element from \(\{1,\dots,N\}\).

In other words, when we count all the elements of \(S\), we eventually run out of elements and come to a stop.

Examples of Finite Things

The number of pencils in your pencil case is finite.

The number of stars in the Milky Way is finite. There are somewhere between 100 and 400 billion of them, but if you had enough time, you could count them and you would eventually come to a stop. Using a computer a bit more powerful than Jasmin's phone might be useful here.

The number of brussels sprouts served up for dinner each year across Australia is finite, even though it sometimes might not seem that way...

What use is infinity, anyway?

Mathematicians sometimes appear treat infinity just like it is a number. You'll definitely come up against this idea when you're finding limits, and it will crop up again when you're finding areas under functions. Let's have a look at some of the rules for 'calculating' with infinity

• The set of real numbers can be written as the interval \( - \infty
• \(\infty + 1 = \infty, \infty + 2 = \infty, \infty + 3 = \infty,\dots\)
• For any real number \(x\), \(x + \infty = \infty\); \(x - \infty = \infty\); \(\infty + x = \infty\); \(\infty - x = \infty\)
• \(\infty + \infty = \infty\); \(-\infty + -\infty = -\infty\)
• \(\infty \times \infty = \infty\); \(-\infty \times - \infty = \infty\); \(-\infty \times \infty = - \infty\)
• For any positive real number \(x\), \(x \times \infty = \infty\); \(x \times - \infty = -\infty\)
• For any negative real number \(x\), \(x \times \infty = -\infty\); \(x \times - \infty = \infty\)

What can't you do to infinity?

Sometimes your maths teacher might come up with a 'proof' of something that's obviously false, like \(1 = 2\), and make your head hurt by asking you what's wrong with it. Usually, the problem is that they've either done something illegal with infinity or something illegal with zero. Let's have a look at a list of things that are forbidden because it's impossible to decide what they mean:

• \( \infty - \infty\)
• \( \infty + -\infty\)
• \( 0 \times \infty\)
• \( 0 \times - \infty\)
• \(\dfrac{\infty}{\infty}\)
• \(\infty^0\)
• \(1^\infty\)

One of those nasty 'proofs'

Let's see why we can't define \(\infty - \infty = 0\). We'll just pretend for a little while that this is fine. We know that \(3 \times \infty = \infty = 2 \times \infty\), and so $$ 0 = \infty - \infty = 3 \times \infty - 2 \times \infty = (3 - 2)\times \infty = \infty. $$ Since \(0 \neq \infty\), we must have done something wrong. The 'something wrong' was assuming that \(\infty - \infty = 0\)!

There are similar nasty 'proofs' that \(1 = 2\), \(1 = 3\) and \(1 = \) anything you like using the false idea that \(\dfrac{\infty}{\infty} = 1\).

Conclusion

Infinity isn't a number. It's the way we express the idea that something goes on forever and ever. Sometimes mathematicians appear to do calculations with infinity, but they have to remember that there are some operations that aren't defined, and others have very different definitions like \(\infty + 1,542 = \infty\). When we do calculations like these, we need to remember that we're actually doing calculations with limits of finite objects, and not with infinity itself.