Notation for Derivatives

Derivatives as Limits

Derivatives tell us how quickly or slowly things change. For example, you might need to find out how quickly the population of bacteria on a pair of sweaty sports socks, left at the bottom of your sports bag, is increasing at any particular instant in time. Derivatives will help you to solve this problem because they tell us about rates of change. As we saw in the introductory article on derivatives, derivatives tell use all about instantaneous rates of change, and can be found by taking the limit of the average rate of change as the time interval gets smaller and smaller.

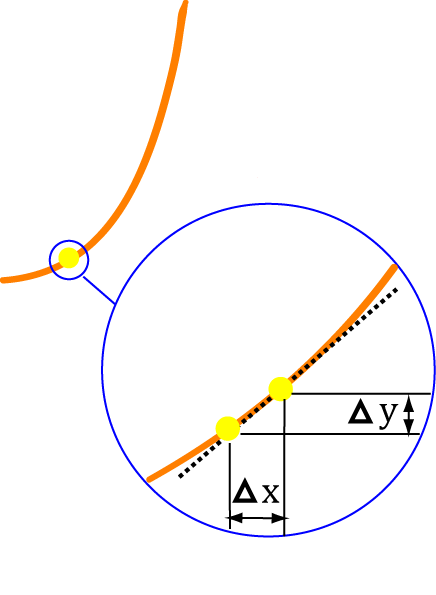
Building up the dy/dx notation

In this article, we're going to explore the notation for derivatives. The introductory article on derivatives looked at how we can calculate derivatives as limits of average rates of change. We're going to use this idea here, but with different notation, so that we can see how Leibniz's notation \(\dfrac{dy}{dx}\) for the derivative is developed.

Start out with a function \(f(x)\) and call it 'y':

\(y = f(x)\)

1. Add \(\Delta x\) and \(\Delta y\) to the picture

When we increase \(x\) by a tiny amount - let's call it \(\Delta x\), \(y\) also increases by a small amount that we'll call \(\Delta y\):

\(y + \Delta y = f(x + \Delta x)\)

2. Find the change in \(y\)

You guessed it, we need to subtract things here! Find the new value of \(y\) minus the old value of \(y\):

\(\begin{align*} y + \Delta y &= f(x + \Delta x)\\ -\;\;\;\;\;\;\;y &= f(x)\\ \hline y + \Delta y - y &= f(x + \Delta x) - f(x) \end{align*}\)

which simplifies to give:

\( \Delta y = f(x + \Delta x) - f(x)\)

3. Now turn it into a rate of change

Remember how to find the average speed of an object? Well, here we want to find the average speed of the change in \(y\), so we divide by the length of our interval: \(x + \Delta x - x =\Delta x\).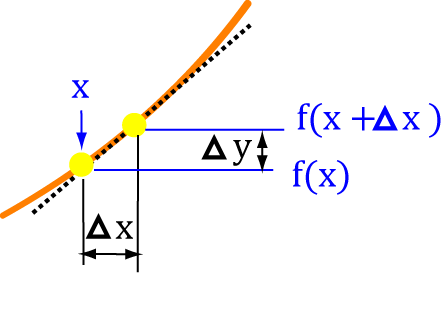

\( \dfrac{\Delta y}{\Delta x} = \dfrac{f(x + \Delta x) - f(x)}{\Delta x}\)

4. Now make \(\Delta x\) really really small

Does this sound like taking a limit? Of course it is, but we don't want to say that. We let \(\Delta x\) approach zero, but instead of using limit notation, we write it as \(dx\):

Test it Out on a Function

Let's try our brand new formula out on the function \(f(x) = x\)

We know the derivative of \(f(x) = x\) is \(f'(x) = 1\), so it looks like it works! Maybe that one was just a bit too easy, though. Let's try another: \(f(x)= x^2\)

We know that the derivative of \(f(x) = x^2\) is \(f'(x) = 2x\), so it worked again!

In practice, we really don't need to go to all this bother to find the derivative of a function, but it's nice to know we can! Usually, we just use the rules of derivatives.