Evaluating Limits

Quick Summary of Limits

Sometimes a function isn’t defined for a particular value of \(x\), but there are ways (called limits) to work out what its value should be at \(x\). Let’s look at one of the examples we explored when we introduced limits. It relies heavily on the idea of ‘closeness’.

Example:

What is the value of \( \displaystyle{\frac{x^2 -4}{x + 2}}\) at \(x = -2\)?

Let's try and plug \(x = -2\) into the equation:

which is BAD because \( \dfrac{0}{0} \) is undefined ( you might see \(\dfrac{0}{0}\) called an indeterminate in some books).

So, we can't find the value of \(\dfrac{x^2 - 4}{x + 2}\) at \( x = -2\). However, we can ask a related question:

Let's look at a table of values and try to work it out:

\(x\)	\(\dfrac{x^2 - 4}{x + 2}\)
-1.5	-3.5
-1.9	-3.9
-1.99	-3.99
-1.999	-3.999
-1.9999	-3.9999
...	...

The values in the table tell use that as \(x\) gets close to \(-2\), \(\dfrac{x^2 - 4}{x + 2}\) gets close to \(-4\).

We'd really like to say that the value of \(\dfrac{x^2 - 4}{x + 2}\) is equal to \(-4\) when \(x = -2\), but we can't because we get an indeterminate form when we plug in \(x = -2\).

Mathematicians have a special word to describe what's going on in this situation: they call \( - 4\) the limit of \(\dfrac{x^2 - 4}{x + 2}\) as \(x\) approaches \(-2\), and write this in symbols as

The graph of \(\dfrac{x^2 -4}{x + 2}\) looks like this:

Do you notice the hole at \(x = -2\)? Even though there's a hole there, you can see that, as the \(x \text{-values}\) get closer to \(-2\), the values of \(\dfrac{x^2 -4 }{x + 2}\) get closer to \(-4\).

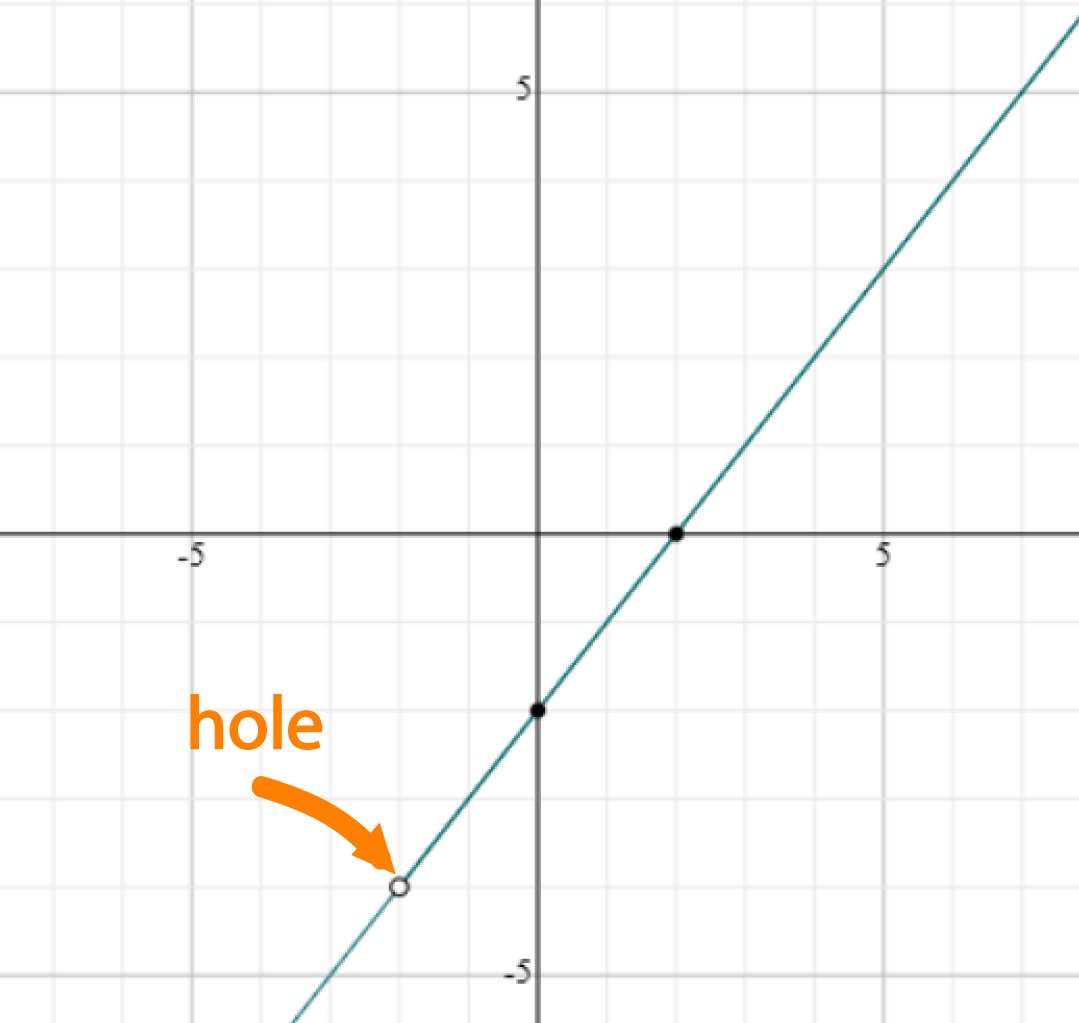
So how do we evaluate limits?

If someone asks you to 'evaluate' a limit, they just want you to find its value. In the example, we said that the limit was \( -4 \) because that's what it looked like it should be. Unfortunately, this wouldn't be good enough for a mathematician. They'd want you to prove that the limit was \(-4\).

Fortunately, this isn't as difficult as it sounds. There are lots of ways that we can find the value of a limit. Let's start with the easiest one and work our way up from there.

1. Substitution

This is the easiest way to evaluate a limit. Just plug the value in! Unfortunately, this doesn't always work, but it's worth a try.

Example:

Evaluate \(\displaystyle{\lim_{x \to 3} \;\frac{x^2}{4}}\).

Try plugging \(x = 3\) into \(\displaystyle{\frac{x^2}{4}}\):

\(\displaystyle{\frac{3^2}{4} = \frac{9}{4}}\) is defined. So \(\displaystyle{\lim_{x \to 3}\;\frac{x^2}{4} = \frac{9}{4}}\)

It's just as easy as that!

But what if it doesn't work? Let's look at another example.

Example:

Evaluate \(\displaystyle{\lim_{x \to -2} \;\frac{x^2 -4}{x + 2}}\)

If we try to plug in \(x = -2\), we end up with

Uh-oh! It doesn't work. We'll have to try something else.

2. Factorisation

If a function is being cantankerous, and won't let you plug a value into it, the answer is often simple. Change the function!

If we factorise the numerator and denominator of a function, we might be able to cancel out some factors from the denominator that cause problems when we try to substitute our \(x\text{-value}\) into it. It's possible that we'll be able to use substitution to find the limit of the new function. If we change the function the right way, the limit of the old function will be the same as the limit of the new function. Let's look at an example.

Example:

Evaluate \(\displaystyle{\lim_{x \to -2} \; \frac{x^2 -4}{x + 2}}\)

We failed miserably when we tried to plug \(x = -2\) into this function, so we'll need to a bit cleverer and try factorising the top and the bottom:

Now notice that the numerator and denominator have a common factor of \((x + 2)\), so we can cancel them out to get a nicely behaved new function: which has the same values as \(\displaystyle{\frac{x^2 -4}{x + 2}}\) everywhere, except at \(x = -2\). It looks like we should be able to use substitution now. What happens if we plug \(x = -2\) into this new function definition?

That's easy! We get \( -2 -2 = -4\), and so

which is exactly what we thought it should be.

3. Multiplying by Conjugates

Sometimes factorisation won't help us to find the value of the limit of a function that is written as a fraction. In that case, it might help to multiply the top and bottom of the fraction by the conjugate of one of them.

Just in case you've forgotten what the conjugate is:
You start with an expression with \(2\) terms in it, and change the sign in the middle of them like this:

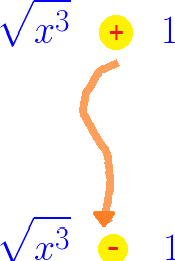
Let's look at an example where conjugation helps us find the limit.

Example

Find

If we try to evaluate this at \(x = 9\), we end up with a \(\displaystyle{\frac{0}{0}}\) situation, which is not a good look! So we need to get a bit cleverer.

Let's try manipulating the function a bit, to see if we can turn it into something more manageable:

• Multiply the numerator and denominator by the conjugate of the numerator:
  
  \(\displaystyle{\frac{3 - \sqrt{x}}{9 - x} \times \frac{3 + \sqrt{x}}{3 + \sqrt{x}}}\)
• Use the difference of two squares \((a + b)(a - b) = a^2 - b^2\) to simplify the top:
  \(\displaystyle{\frac{3^2 -(\sqrt{x})^2}{(9 - x)(3 + \sqrt{x})}}\)
• Simplify the numerator further:
  \(\displaystyle{ \frac{ (9 - x)}{(9 - x)(3 + \sqrt{x})}}\)
• Do some cancellation:
  \(\displaystyle{\frac{1}{3 + \sqrt{x}}}\)

Now we can calculate the limit!

We turned the cantankerous function \(\displaystyle{\frac{3 - \sqrt{x}}{9 - x}}\) into the nice friendly function \(\displaystyle{\frac{1}{3 + \sqrt{x}}}\), and were then able to calculate the limit by substitution.

4. Limits to infinity and rational functions

Rational functions have the form \(\displaystyle{f(x) = \frac{p(x)}{q(x)}}\), where \(p(x)\) and \(q(x)\) are polynomials.

For example, \(f(x) = \displaystyle{\frac{x^3 + 4x + 5}{3x^4}}\) is a rational function with \(p(x) = x^3 + 4x + 5\) and \(q(x) = 3x^4\).

We're often interested in what happens to the values of rational functions for very large values of \(x\). We write this as \(\displaystyle{\lim_{x \to \infty}\; \frac{p(x)}{q(x)}}\)