Differentiation has many useful applications. For example, you might need to know the rate of bacterial growth on that pair of sweaty socks you left at the bottom of your sports bag, or Gus the snail's instantaneous speed in his latest attempt at the land-speed record. There are other more standard applications, like finding the slope of a graph at a particular point, or the maximum and minimum values of a demand function. Fortunately, we don't always need to pull out the limits to calculate these things. Instead, we can apply the rules of differentiation. The purpose of this article is to give you a summary of these rules, and a few examples of their application. Other articles will discuss the power rule, chain rule, product rule and quotient rule in more depth.

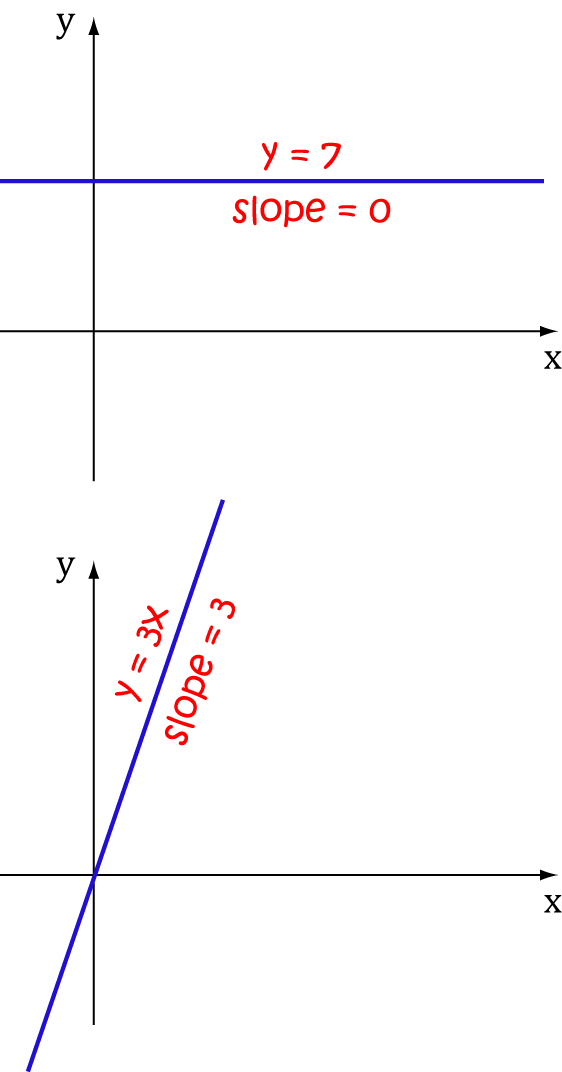
Let's start with a couple of examples. Don't forget that the little prime mark ' means "the derivative of".

Derivatives of Commonly Occurring Functions

So that you don't have to continually pull out the limits to find the derivatives of commonly occurring functions, let's write a list of their derivatives that you can refer back to whenever you feel the need.

Function description	Function expression	Derivative
Constant Function (\(k\) is for 'konstant')	\(\displaystyle{ k }\)	\(0\)
Straight Line	\(\displaystyle{ x }\)	\(1\)
	\(kx\)	\(k\)
	\(mx + b\)	\(m\)
Square	\(\displaystyle{x^2}\)	\( 2x\)
Square Root	\(\sqrt{x} = x^{\frac{1}{2}}\)	\( \dfrac{1}{2}x^{-\frac{1}{2}} = \dfrac{1}{2 \sqrt{x}}\)
Exponentials	\(a^x\)	\( a^x \ln (a)\)
	\(e^x\)	\(e^x \ln (e) = e^x\)
Logarithms	\(\ln(x)\)	\( \dfrac{1}{x}\)
	\(\log_b(x)\)	\( \dfrac{1}{x \ln(b)}\)
Trig functions (don't forget \(x\) is measured in radians!)	\( \sin x \)	\(\cos x\)
	\(\cos x \)	\(-\sin x \)
	\(\tan x\)	\(\sec^2 x\)
Inverse Trig Functions (don't forget the restrictions on the domain)	\( \sin^{-1}(x) \)	\(\dfrac{1}{\sqrt{1 - x^2}}\)
	\( \cos^{-1}(x) \)	\(-\dfrac{1}{\sqrt{1 - x^2}}\)
	\(\tan^{1} (x)\)	\(\dfrac{1}{1 + x^2}\)

Rules of Differentiation

And now for the rules that help you stitch the above derivatives together to come up with the derivatives of some really impressive-looking functions. Differentiation is a great party trick!

Name of Rule	Function expression	Expression for Derivative
Multiplication by a constant	\( kf(x)\)	\(k f'(x)\)
Power Rule (\(n \neq -1\))	\(x^n\)	\(nx^{n-1}\)
Sum and Difference Rules	\((f + g)(x)\)	\(f'(x) + g'(x)\)
Product Rule	\(fg\)	\(fg' + f'g\)
Quotient Rule	\(\dfrac{f}{g}\)	\(\dfrac{gf' - fg'}{g^2}\)
Chain (or function of a function) Rule using ' notation	\(f(g(x))\)	\(f'(g(x))g'(x)\)
Chain Rule using Leibniz notation	\(y = f(u(x))\)	\(\dfrac{dy}{dx} = \dfrac{dy}{du}\cdot \dfrac{du}{dx} \)
Chain Rule using function composition notation	\(f \circ g\)	\((f' \circ g) \times g'\)
Reciprocal Rule (or just use the chain and power rules)	\(\dfrac{1}{f}\)	\(-\dfrac{f'}{f^2}\)

Examples of applying the rules

Let's finish by using the rules to find the derivatives of some functions. Don't forget that the table of common derivatives will be a big help here.

Example 1

Find the derivative of \(\displaystyle{\tan (x)}\).

In the table of common derivatives, the derivative of \(\tan (x)\) is listed as \(\sec^2(x)\). So

Example 2: applying the power rule

Find \( \dfrac{d}{dx}(x^4) \).

Use the power rule with \(n = 4\):

Watch out! Lots of students get confused here and apply the power rule for integrals. Try to remember: when you're differentiating, the power of \(x\) goes down ("d" for "differentiation").

Example 3: more on the power rule - negative indices

Find \(\dfrac{d}{dx}\left(\dfrac{1}{x^2}\right)\).

Remember your index laws: \(\dfrac{1}{x^2}= x^{-2}\), so we can use the power rule here.

Example 4:constant multiplication

Find \(\displaystyle{\frac{d}{dx} (17x^4)}\).

Bring the \(17\) out to the front of the derivative:

Now use the power rule on \(x^4\):

Example 5: the derivative of a sum (difference) is the sum (difference) of the derivatives

Find \(\displaystyle{\frac{d}{dx}(x^3 + x^2 - x^6)}.\)

The sum and difference rules say

So, we can work out each derivative separately, and then add (or subtract) them. Using the power rule gives

• \(\dfrac{d}{dx}(x^3) = 3x^2\)
• \(\dfrac{d}{dx}(x^2) = 2x\)
• \(\dfrac{d}{dx}(x^6) = 6x^5\)

So,

Example 6: using the product rule

Find \(\displaystyle{\frac{d}{dx} x^2\cos(x)}\).

The product rule says

In this example, \(f(x) = x^2\) and \(g(x) = \cos(x)\). By the power rule, \(f'(x) = 2x\) and the table of common derivatives gives \(g'(x) = - \sin (x)\). So

Example 7: using the quotient rule

Find \(\displaystyle{\frac{d}{dx} \left(\frac{\sin x}{x^2 + x}\right)}\).

The quotient rule says

In this example, \(f(x) =\sin (x) \) and \(g(x) = x^2 + x\). The table of common derivatives tells us that \(f'(x) = \cos (x)\), and applying the power and sum rules gives \(g'(x) = \dfrac{d}{dx}(x^2) + \dfrac{d}{dx}(x) = 2x + 1\). So,

Example 8: using the chain rule

We'll just use one form of the chain rule for now. We'll explore several different examples of the application of the chain rule in the article on the chain rule.

Find \(\displaystyle{\frac{d}{dx} (\sin(x^3))}\)

The chain rule says

In this example, \(f(x) =\sin (x) \) and \(g(x) = x^3\). The table of common derivatives tells us that \(f'(x) = \cos (x)\), and applying the power rule gives \(g'(x) = \dfrac{d}{dx}(x^3) = 3x^2\). So, by the chain rule