Integration by Substitution

We can use integration by substitution to undo differentiation that has been done using the chain rule. It gives us a way to turn some complicated, scary-looking integrals into ones that are easy to deal with. To use this technique, we need to be able to write our integral in the form shown below:

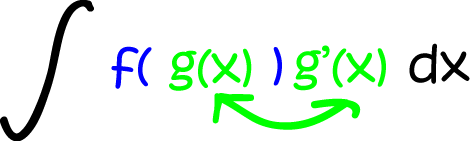
Do you notice how the \(g(x)\) inside the blue brackets matches up with the \(g'(x)\) outside the blue brackets?

Here's a real-life example:

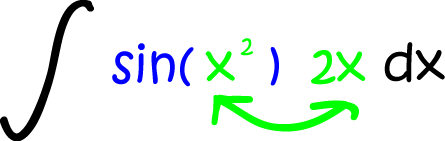
In the above example, \(f = \sin\) and \(g(x) = x^2\). The derivative \(g'(x) = 2x\) is precisely what appears at the end of the integrand. So, this example is in good shape and ready for us to apply our brand new, fancy-shmancy integration technique.

So, what do we do now? I'm glad you asked. We do our substitution. Replace \(g(x)\) by \(u\) and \(g'(x)\;dx\) by \(du\) just as in the image below:

Because we most often substitute a \(u\) for \(g(x)\), integration by substitution is sometimes called "u-substitution". (I've actually only ever seen this in an American book). Of course, we could also substitute in a penguin for \(g(x)\), and then call it "penguin-substitution"... but I think it's probably easiest to simply call it "substitution".

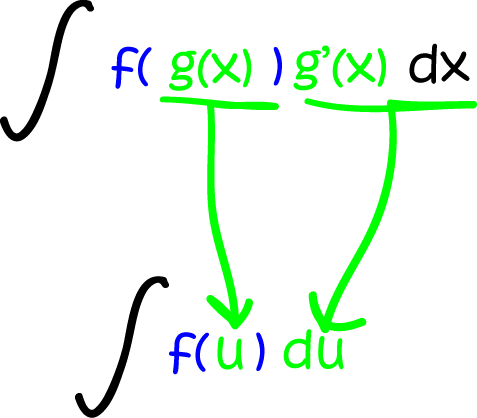
The next step is to integrate the (hopefully simpler) function \(f(u)\) with respect to \(u\). Once that is done we have do another substitution - we plug the expression for \(g(x)\) into our antiderivative whereever we see \(u\). So, here's a question for you... why don't the Americans call it \(g(x)\)-substitution?

Now it's time to put our theory into practice. Let's see if we can integrate our real-life example.

Example

Find

This one is nicely set up for substitution:

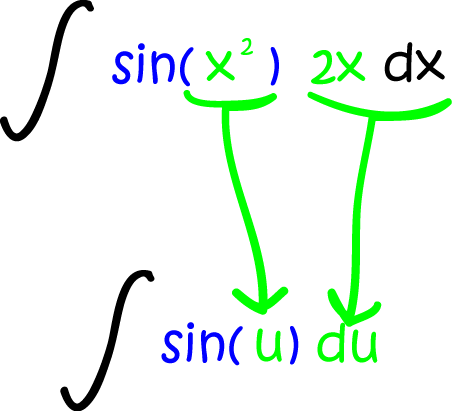
So now we can integrate

Finally plug \(u = x^2\) back in to give:

Now let's try some slightly harder examples - ones that aren't quite so nicely set up for substitution.

Example

Find

This integrand wasn't quite so thoughtful in the way it expressed itself. If we set \(u = x^2\), then its derivative is \(2x\). But we have \(8x\). There's no need to panic. The rules of integration get us out of trouble here. All you need to do is pull a 4 out the front of the integral, like this:

If you're not sure why this is OK, check out the "multiplication by a constant" rule in the rules of integration article. Don't worry, we'll still be here when you get back!

Sorted? Let's go on. Now all we have is continue as before to give

Finally plug \(x^2\) back in for \(u\) to give:

Time for another? Let's try one that's trickier still.

Example

Find

Usually when you have a rational function to integrate, you want to set \(u = \text{denominator} = x^3 + 1\). But in this case, the derivative of \(x^3 + 1\) is \(3x^2\), which isn't what this function has upstairs. This is OK: all we need to do is to put \(3x^2\) up top and multiply the whole integral by \(\dfrac{1}{3}\) so that our new additions cancel each other out. If you're not sure why this is OK, check out the "multiplication by a constant" rule in the rules of integration article. Here we go:

Now we're in business! Let's do the substitution:

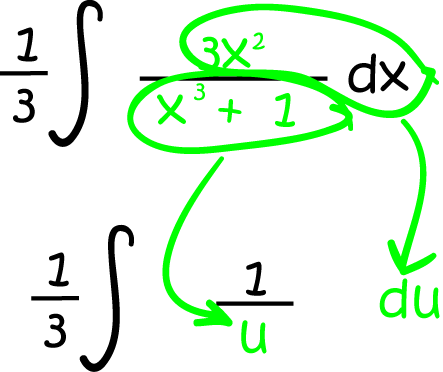
Now use our rules of integration to integrate:

Finally, plug \(u = x^3 + 1\) back in:

Let's look at one last example. At first, it doesn't look like substitution will work on this one, but it will.

Example

Find

If you want to, you can always use the binomial theorem to expand the integrand. But this is an article on integration by substitution, so that's what we'd better do. The obvious thing to do seems to be to set \(u = x + 7\). Will this work for us? We need our integrand to include a function of \((x + 7)\) multiplied by the derivative of \((x + 7)\), and there's nothing but \((x + 7)^4\) in the integrand. Don't panic! The derivative of \((x + 7)\) is just \(1\) (if you look carefully, there's a little \(1\) hiding somewhere beside the \(dx\)). So, we have

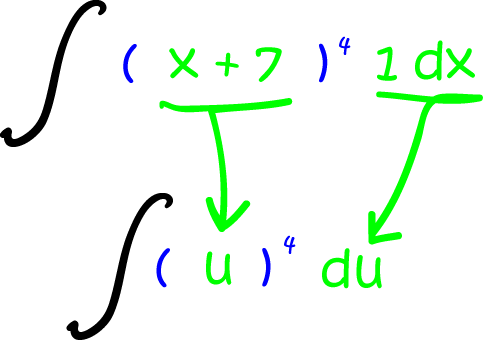
Integrating gives:

Now to get rid of the \(u\) (plug in \(u = x + 7\)):

Summary

We now have something else to add to our list of integration party-tricks. Integration by substitution helps us to turn mean, nasty, complicated integrals into nice, friendly, cuddly integrals that we can evaluate. Remember the steps:

1. Start with an integral of the form:
   
   
   
   
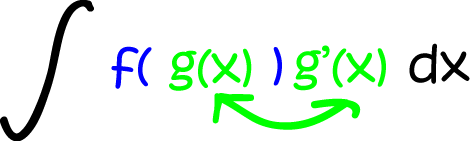
2. Set \(u = g(x)\), and differentiate \(u\) to find \(du = g'(x)\;dx\).
3. Integrate \(\displaystyle{\int f(u)\;du}\)
4. Replace \(u\) by \(g(x)\) wherever you see it in the integral.

No problem, right? Actually, the hardest part is working out what to let \(u\) equal. The best thing to do is to get plenty of practice. Have fun!