Calculus
Chapters
Cross Sections
Cross Sections
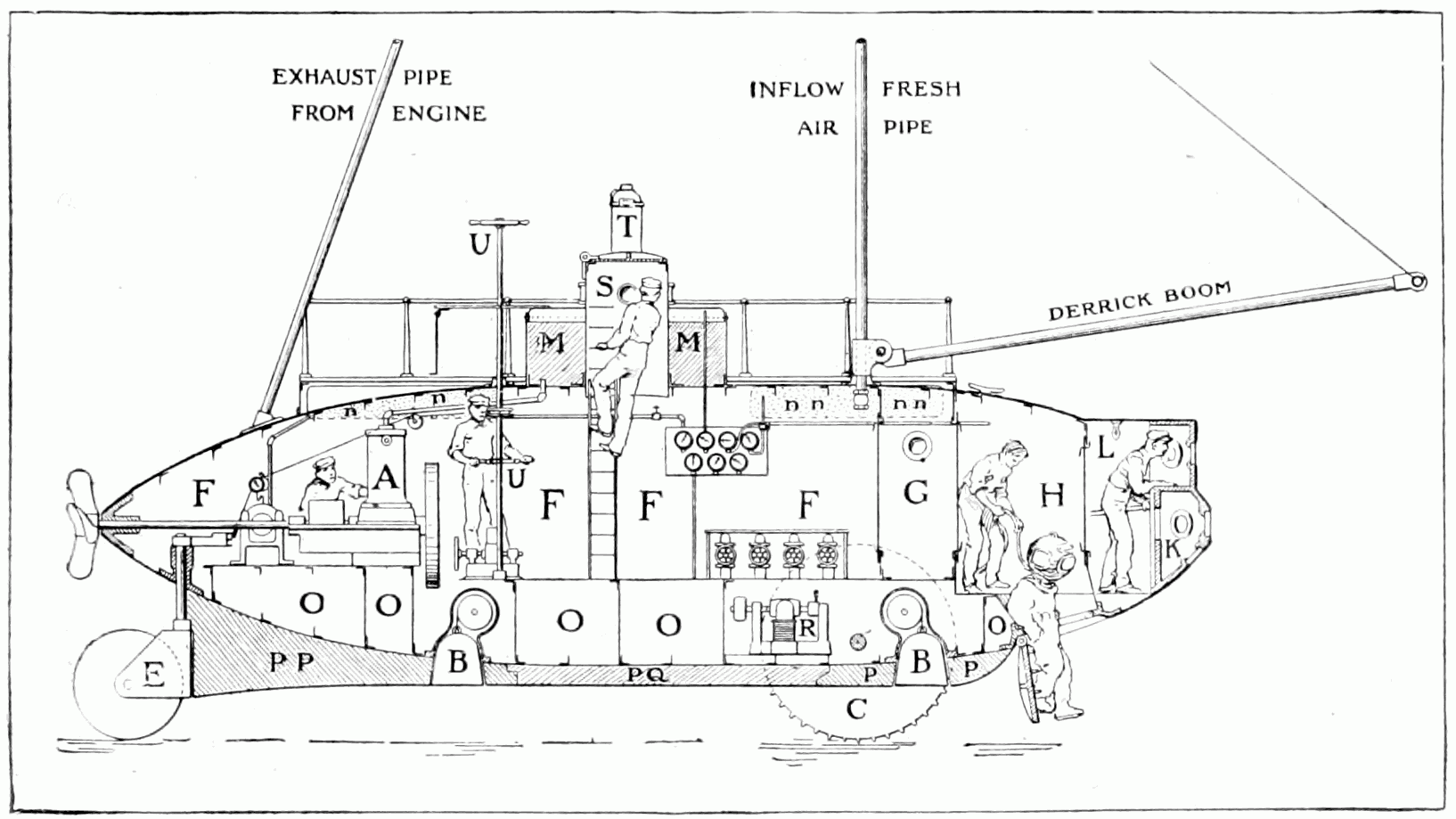
Sam has a cool book that shows you cross-sections of different early marine vessels. My favourite is the cross section of an early submarine shown on the left.
Can you imagine what it would have been like to work in one of these? You could barely stand up. I suspect you couldn't stay down for long, either, because you needed to get fresh
air through the inflow pipe.
A cross-section is a view of an object formed by taking a slice through it. For example, there's a cross-section of a cabbage shown below. We frequently talk about cross-sections in geometry, but they are of interest in many different fields such as medicine and architecture.

Cross-sections in Geometry
Surprisingly enough, because this is an article about mathematics, we're going to concentrate on cross-sections in geometry. In geometry, a cross-section is the shape
formed when we cut through a 3-dimensional object with a plane. If someone asks you to draw a cross-section, you only need to draw the shape formed when you cut through the object,
not the whole 3D-shape. Most of the time (but not always) we take cross-sections that are parallel to the base of the object. Let's have a look at a few examples.
For example, the cross-sections of this hexagonal prism, parallel to the base are all hexagons
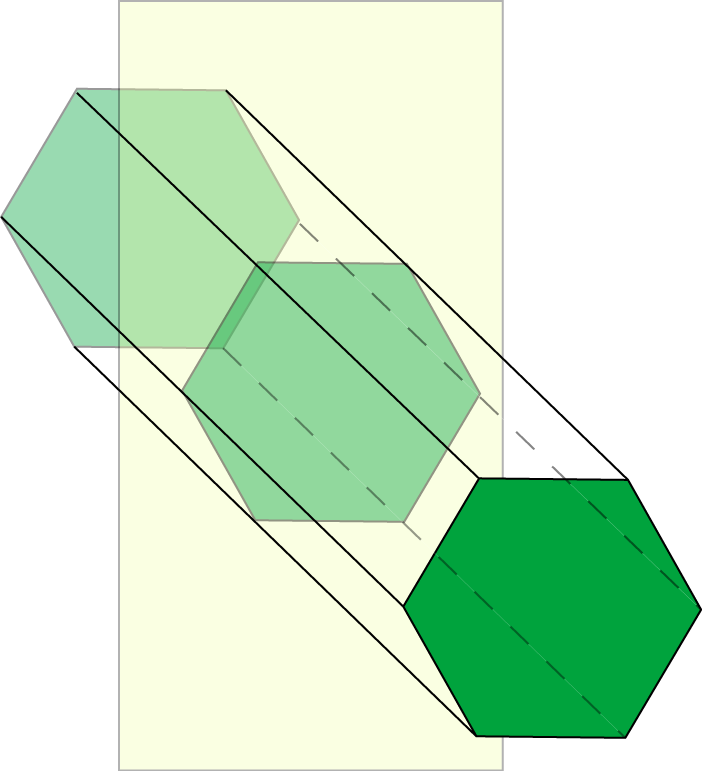
You can take cross-sections of a 3-dimensional shape in any direction, not just parallel to the base.

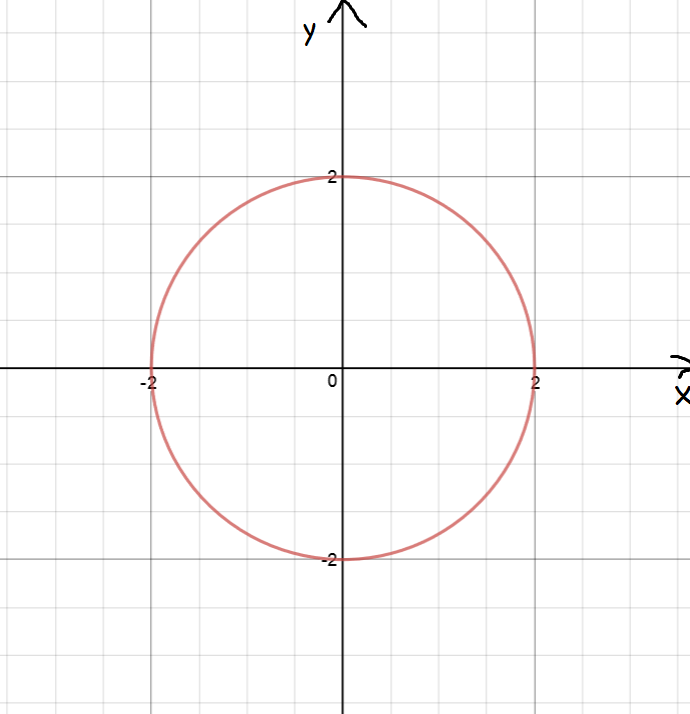
For example, every cross-section of a sphere, in every direction is a circle. The circles may vary in size, depending on where you take the cross-section, but they
are all circles. The largest cross-sections are called the great circles of the sphere.
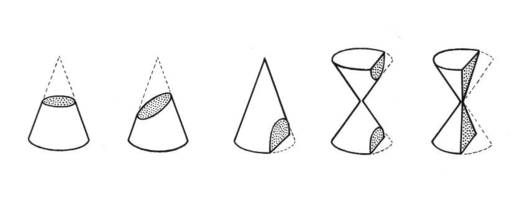
If you take cross-sections of a cone in different directions, you get a number of different shapes. These include circles, ellipses, hyperbolas and parabolas. They
are so interesting to mathematicians that they have been given a special name: conic sections. You can read more about these shapes in the article on conic sections.
Cross-sections of More 3-D Shapes
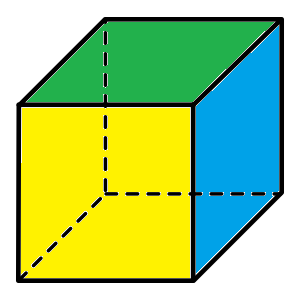
The cross-sections of a cube parallel to one of its faces are squares.


The cross-sections of a (circular) cylinder, parallel to its bases are circles. All have the same radius as the cylinder.
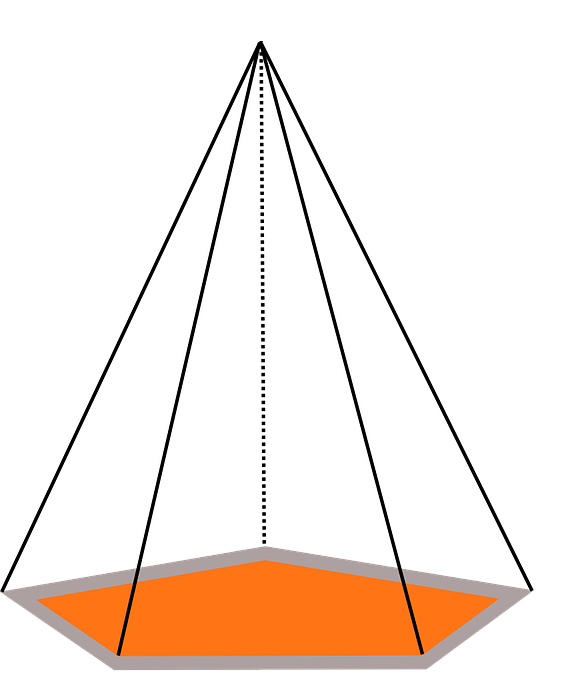
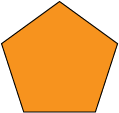
The cross-sections of this pentagonal pyramid, parallel to the base are pentagons. They have different sizes, depending on how far up the pentagonal pyramid the cross-section is taken, but all are similar to the base.
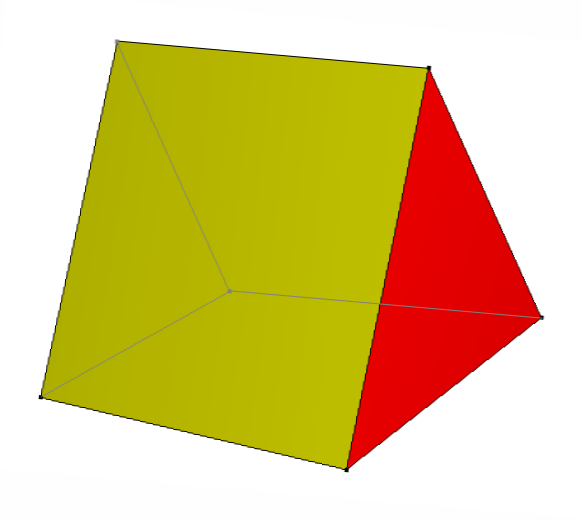
Like all prisms, the cross-sections of this triangular prism, parallel to the base, all have the same size and shape as its base. They are all triangles.

Description
Calculus is the branch of mathematics that deals with the finding and properties of derivatives and integrals of functions, by methods originally based on the summation of infinitesimal differences. The two main types are differential calculus and integral calculus.
Environment
It is considered a good practice to take notes and revise what you learnt and practice it.
Audience
Grade 9+ Students
Learning Objectives
Familiarize yourself with Calculus topics such as Limits, Functions, Differentiability etc
Author: Subject Coach
Added on: 23rd Nov 2017
You must be logged in as Student to ask a Question.
None just yet!