Reading:

Calculus

Chapters

An Introduction to Calculus

Calculus is all about the rates at which things change. For example, you might want to measure the change in the amount of time your parents spend nagging you to do your homework as you get older. This would be measured using the slope of the nagging duration function. Jasmin and Al are down at the park at the moment. They're wondering about a rate of change: how fast Al can run at any instant in time. Perhaps a little calculus would help them. Let's watch them and see.

An Introduction to Calculus

Al is in training for an athletics competition, and Jasmin is timing his laps with her stop watch...

Al: How fast am I going now, Jasmin?

Jasmin: You completed that lap in 80 seconds, so you're doing 5 metres per second.

Al: No, I mean right now.

Jasmin: OK, you're on the straight now, so I'll time you for 100 metres...that took 18 seconds. Now you're doing about 5.5 metres/second.

Al: No, Jasmin. I don't want my average speed for 100 metres. I want my speed right now!

Jasmin: OK, I'll measure it as you pass that wattle tree over there.

An Introduction to Calculus

Jasmin: Right, you were at the wattle tree for zero seconds, and you ran zero metres. So your speed as you passed the wattle tree was ... I can't calculate it, Al, because you can't divide by zero!

Al: Aarrggggghhhhh! (trips on his shoelace and falls)

An Introduction to Calculus

Jasmin: (giggling) Hey, Al! I know how fast you're going now: \(0 \text{ metres/second}\)!

Al groans and shakes his head.

Jasmin is quite right. The only speed that she can come up with using a stopwatch is an average speed as Al runs a certain distance. Al wants to know his instantaneous speed, something that is only possible to determine using calculus.

Let's go and visit Alice the cow. It sounds like she's up to her thrill-seeking tricks again!

Alice the Cow at the Circus

Alice the cow is practising one of her circus tricks.

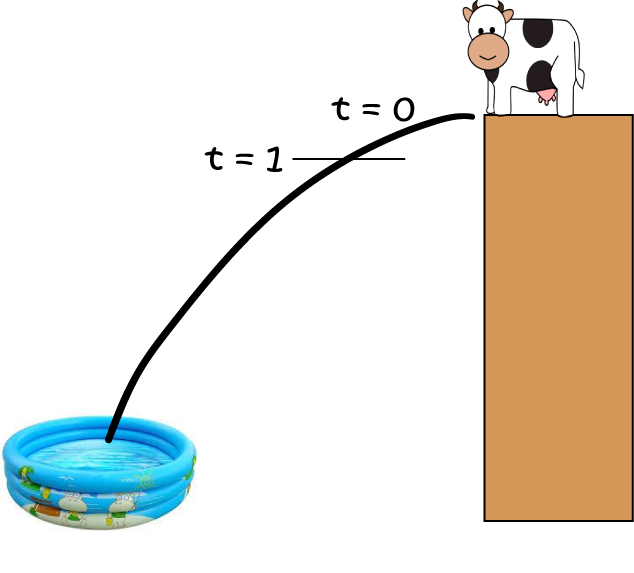An Introduction to Calculus Alice needs to jump off a platform that is \(15 \text{ metres}\) high and land in a wading pool at the bottom. Jasmin, knowing that Alice is an extremely talented mathematician, asks Alice how fast she will be falling after 1 second.

As she knows that the acceleration due to gravity is about \(9.8 \text{ metres/second}^2\), Alice uses the formula

\(d = \dfrac{1}{2} gt^2 = 4.9 t^2 \)

to find the distance \(d\) (in metres) that she falls in \(t \text{ seconds}\). She works out that she falls \(4.9 \text{ metres}\) in \(1\) second.

Jasmin wants to know Alice's speed. As speed is equal to distance divided by time, Jasmin calculates that at \(t = 1 \text{ second}\):

\( \text{speed} = \dfrac{\text{distance}}{\text{time}} = \dfrac{4.9 \text{ metres}}{1 \text{ second}} = 4.9 \text{ m/s}. \)

However, she realises that this is still only the average speed. She wonders what will happen if she tries to find the speed at exactly one second:

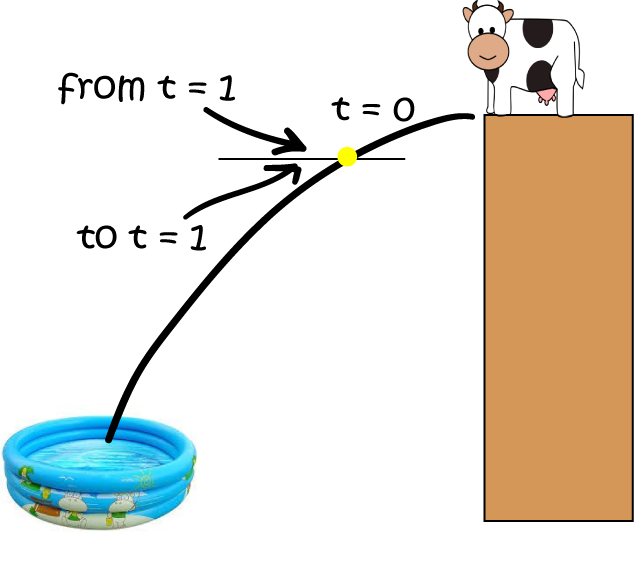An Introduction to Calculus At exactly 1 second Alice's speed is going to be equal to

\( \text{speed} = \dfrac{\text{distance}}{\text{time}} = \dfrac{4.9 - 4.9 \text{ metres}}{1 - 1\text{ second}} = \text{ undefined}. \)

Oh, no! There's that pesky division by zero problem again. What should Jasmin do?

Let's have a think about this. If you try to figure out a speed at a particular instant in time, then you really have nothing to work with: you can't travel any distance in no time. Alice makes a suggestion. As I said, she is an extremely talented mathematician as well as a thrill seeker. Why not invent a very short time, and call it \(\Delta t\)? This time should be shorter than anything you can think of, but not equal to zero. Then, work out the distance travelled between time \(t\) and time \(t + \Delta t\). You know, this could work! Let's see what happens.

After \(1 \text{ second}\), Alice has fallen:

\( 4.9 (1)^2 = 4.9 \text{ metres}\)

After \(1 + \Delta t \text{ seconds}\), Alice has fallen:

\( 4.9 (1 + \Delta t)^2 \text{ metres} = 4.9 (1 + 2 \Delta t + (\Delta t)^2 ) \text{ metres} = 4.9 + 9.8 \Delta t + 4.9(\Delta t)^2 \text{ metres}\)

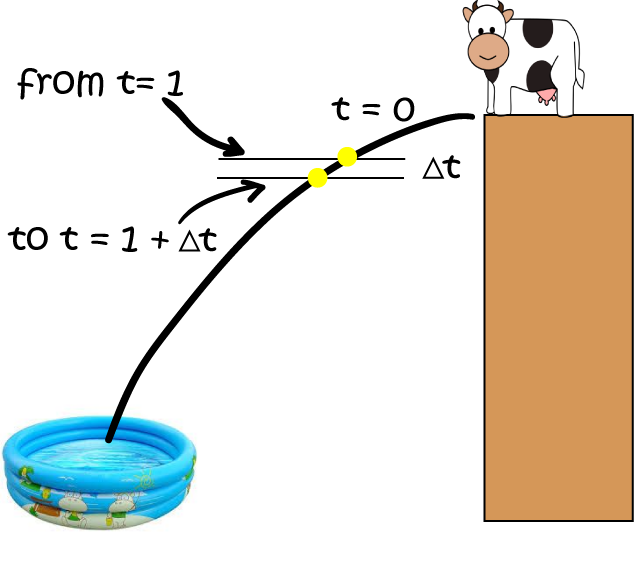
An Introduction to Calculus

So, the change in distance between \(1 \text{ second}\) and \(1 + \Delta t \text{ seconds}\) is:

\( \begin{align*} \text{Change in d} &= (4.9 + 9.8 \Delta t + 4.9(\Delta t)^2) - 4.9 \text{ metres}\\ &= 9.8 \Delta t + 4.9 (\Delta t)^2 \text{ metres} \end{align*} \)

Now we can divide this distance by the time to get the average speed for the time interval from \(1 \text{ second}\) to \(1 + \Delta t \text{ seconds}\):

\( \begin{align*} \text{Speed } &= \frac{9.8 \Delta t + 4.9 (\Delta t)^2 \text{ metres}}{\Delta t \text{ seconds}}\\ &= 9.8 + 4.9 \Delta t \text{ metres/second}. \end{align*} \)

Now, Jasmin has a think. She wants to find an instantaneous speed, so the time interval between \(1 \text{ second}\) and \(1 + \Delta t \text{ seconds}\) has to be very very small. The solution: let \(\Delta t\) shrink towards zero. Then, what happens to the speed? The \(4.9 \Delta t\) term also shrinks towards zero. So Jasmin finds the instantaneous speed!

\( \begin{align*} \text{Speed } = 9.8 \text{ metres/second}. \end{align*} \)

Jasmin is feeling pretty chuffed. She tells Al about it at school the next day. She now knows how to find his instantaneous speed at any time as he runs around the oval. Jasmin has started to learn how to use calculus.

What is Calculus

The word calculus comes from the Latin word for a small pebble or stone used in counting. When we do calculus, we are breaking up things into small chunks called "infinitessimals". We are interested in two main branches of calculus. They are, essentially, opposites of each other (one undoes the other):

Differential Calculus: This branch of calculus breaks things up into small chunks to study its rate of change, e.g. a speed.
Integral Calculus: In integral calculus, we add the little chunks back together by taking integrals. This helps us to work out how much of something there is in total. For example, we might need to find the distance travelled over a certain time period.

Jasmin and Alice were doing differential calculus when they broke the time interval for Alice's jump up into tiny chunks called \(\Delta t\). Let's have a look at another example. This time, there'll be no risk to Alice or to the wading pool.

Example

What is the slope of the function \(y = x^4\) at the point \(x = 1\) ?

Let's try Alice's trick with a tiny chunk of \(x\) called \(\Delta x\):

At \(x = 1\), \(y = (1)^4 = 1\).
At \(x = 1 + \Delta x\), \(y = (1 + \Delta x)^4 = 1 + 4\Delta x + 6 (\Delta x)^2 + 4 (\Delta x)^3 + (\Delta x)^4.\)

So the change in \(y\)-values as \(x\) changes from \(1\) to \(1 + \Delta x\) is:

\( \begin{align*} \text{Change in y} &= (1 + 4\Delta x + 6 (\Delta x)^2 + 4 (\Delta x)^3 + (\Delta x)^4) - 1\\ &= 4\Delta x + 6 (\Delta x)^2 + 4 (\Delta x)^3 + (\Delta x)^4, \end{align*} \)

and the slope is

\( \begin{align*} \text{slope} &= \dfrac{4\Delta x + 6 (\Delta x)^2 + 4 (\Delta x)^3 + (\Delta x)^4}{\Delta x}\\ &= 4 + 6 \Delta x + 4 (\Delta x)+ (\Delta x)^3 \end{align*} \)

Finally, let \(\Delta x\) get really really small (approach zero) to give an instantaneous slope of \(4\).

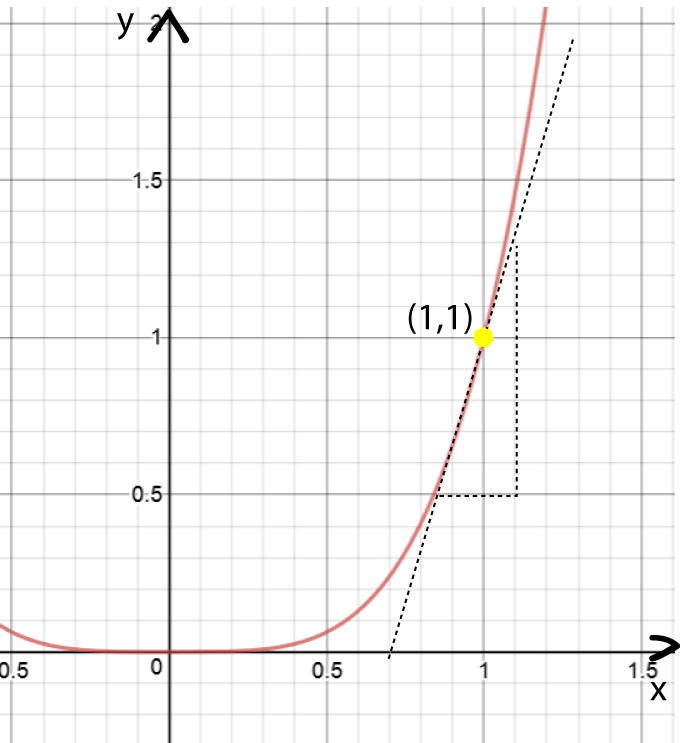An Introduction to Calculus Let's check this out on the graph of \(y = x^4\). As you can see on the right, the slope of the graph is changing all the time, but if we draw a tangent to the graph at the point \((1,1)\), it does have a slope of 4. So our "calculus" looks like it gave us the right answer

Try some for yourself

Why not see if you can find the slope of functions like \(f(x) = x^3\) and \(f(x) = x^2\) at the point \((1,1)\)? Of course, you can pick other points as well. I just chose this one because it made the arithmetic easy.

Most importantly, have fun!

Description

Calculus is the branch of mathematics that deals with the finding and properties of derivatives and integrals of functions, by methods originally based on the summation of infinitesimal differences. The two main types are differential calculus and integral calculus.

Environment

It is considered a good practice to take notes and revise what you learnt and practice it.

Audience

Grade 9+ Students

Learning Objectives

Familiarize yourself with Calculus topics such as Limits, Functions, Differentiability etc

Author: Subject Coach
Added on: 23rd Nov 2017

You must be logged in as Student to ask a Question.

None just yet!

Calculus

Chapters

An Introduction to Calculus

An Introduction to Calculus

Alice the Cow at the Circus

What is Calculus

Example

Try some for yourself

Description

Environment

Audience

Learning Objectives

THANK YOU FOR STOPPING BY!