The Chain Rule for Derivatives

Introduction

Calculus is all about rates of change. To find a rate of change, we need to calculate a derivative. In this article, we're going to find out how to calculate derivatives for functions of functions.

Let's start by thinking about a useful real world problem that you probably won't find in your maths textbook.

A politician, Barton Lambert, proposes to solve temporary wool shortages in Australia by building a suspension bridge to New Zealand. His idea is that sheep will be herded across the bridge for shearing in Australia and then herded back to New Zealand. An engineer working on the project is concerned about oscillations in the bridge. He believes that the oscillations of the bridge at time \(t\) will satisfy the equation \(\text{wobble}(t) = 3\sin(t^3) \text{ cm}\), where \(t\) is measured in hours and wants find the rate of change of the oscillations after \(10\) hours.

This means that he would need to find the derivative of the function \(\text{wobble}(t) = 3\sin(t^3)\), and evaluate it at \(t = 10\).

Sounds easy enough, but how do we find the derivative of \(\text{wobble}(t)\)?

The Chain Rule

The engineer's function \(\text{wobble}(t) = 3\sin(t^3)\) involves a function of a function of \(t\). There's a differentiation law that allows us to calculate the derivatives of functions of functions. It's called the Chain Rule, although some text books call it the Function of a Function Rule.

So what does the chain rule say?

There are a few ways of writing it. Perhaps the one you see most commonly in introductory calculus text books is this:

The derivative of \(f(g(x))\) is given by \(f'(g(x))\cdot(g'(x)).\)

A second way, using Leibniz's notation for the derivative is:

If \(y\) is a function of \(u(x)\), then \(\dfrac{dy}{dx} = \dfrac{dy}{du} \cdot \dfrac{du}{dx}.\)

Finally, if you want to look like you're extremely clever, you can state the chain rule in terms a composition of functions. Remember that the funny "fog(x)" notation, \(f \circ g\) is defined by \(f \circ g (x) = f(g(x))\). So, the chain rule is stated as:

The derivative of \(f \circ g\) is \((f' \circ g) \times g'\).

Now let's differentiate a few functions using the chain rule

Example

If \(h(x) = \cos(x^2)\), what is \(h'(x)\)?

The function \(\cos(x^2)\) is a function of a function. It's made up of the functions \(\cos()\) and \(x^2\). So we need to apply the chain rule as follows:

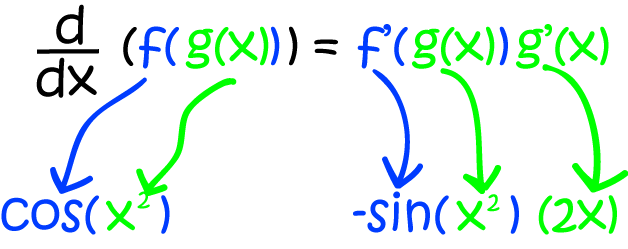
\(h'(x) = -2x \sin (x^2)\).

Let's try this again using another version of the chain rule:

\(\dfrac{dy}{dx} = \dfrac{dy}{du} \cdot \dfrac{du}{dx}\)

Here, \(u = x^2\) and \(y = \cos(u) \). Differentiating each function gives:

\( \dfrac{d}{du} (\cos(u)) = - \sin (u)\) and \(\dfrac{d}{dx} (x^2) = 2x \),

So, applying the chain rule gives:

\( \dfrac{dy}{dx} = -\sin(x^2) \cdot (2x) = - 2x \sin(x^2) \).

That wasn't too bad, was it? Let's try another example:

Example

Find the derivative of \(h(x) = \dfrac{1}{\sin x}\).

We set \(f(x) = \dfrac{1}{x}\) and \(g(x) = \sin x\). Then \(f'(x) = \dfrac{- 1}{x^2}\), and \(g'(x) = \cos x\) (check these in the rules of derivatives article if you don't remember them). Now use the chain rule to find:

Time for another one?

Example

Find the derivative of \(h(x) = (7x^2 - 8x)^4 \).

This time, we set \(f(x) = x^4\) and \(g(x) = 7x^2 - 8x\). Then \(f'(x) = 4x^3\), and \(g'(x) = 14x - 8\) (using the power rule, constant multiplication and difference rules). Now use the chain rule to find:

Let's look at one last example, and then it'll be time to deal with our woolly problem.

Example

Find the derivative of \(h(x) = \ln(x^3 + 5x)\).

We set \(f(x) = \ln(x)\) and \(g(x) = x^3 + 5x\). Then \(f'(x) = \dfrac{1}{x}\), and \(g'(x) = 3x^2 + 5\) (check these in the rules of derivatives article if you don't remember them). Now use the chain rule to find:

A Questionable Solution to the Wool Shortage Problem

Now we know enough to solve our engineer's problem. The bridge will oscillate by

at time \(t\) hours, and he wants to know the speed of the oscillations after \(t = 10 \text{hours}\). So, he needs to find the derivative of the \(\text{wobble}\) function and plug in \(t = 10\). It looks like a job for the chain rule!

Set \(f(t) = 3 \sin (t)\) and \(g(t) = t^3\). Then \(f'(t)= 3 \cos (t)\), and \(g'(t) = 3t^2\) by the power rule. So, applying the chain rule,

At \(t = 10\):

Oscillations like this are likely to break the bridge. To see this in action, search for "Tacoma Narrows Bridge" on the internet.

So, the engineer was right to be concerned. Apart from the infeasibility of constructing such a long bridge and herding sheep over it, Barton Lambert's idea is downright dangerous!