Points of Inflection

Introduction

Points of Inflection are points where a curve changes concavity: from concave up to concave down, or vice versa. Just to make things confusing, you might see them called Points of Inflexion in some books. Call them whichever you like... maybe you think it's quicker to write 'point of inflexion'. Of course, you could always write P.O.I for short - that takes even less energy.

Purely to be annoying, the above definition includes a couple of terms that you may not be familiar with. If you're wondering what on earth concave up and concave down, rest assured that you're not alone. Let's draw some pictures so we can get a better idea:

The following pictures show some more curves that would be described as concave up or concave down:

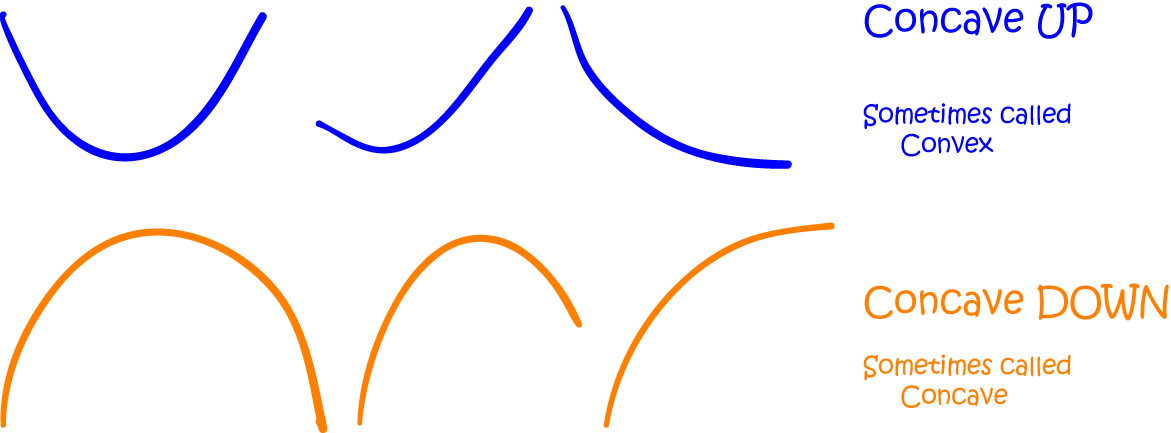
Do you want to know more about concave up and concave down functions? The article on concavity goes into lots of gory details.

Finding Points of Inflection

To find a point of inflection, you need to work out where the function changes concavity. That is, where it changes from concave up to concave down or from concave down to concave up, just like in the pictures below.

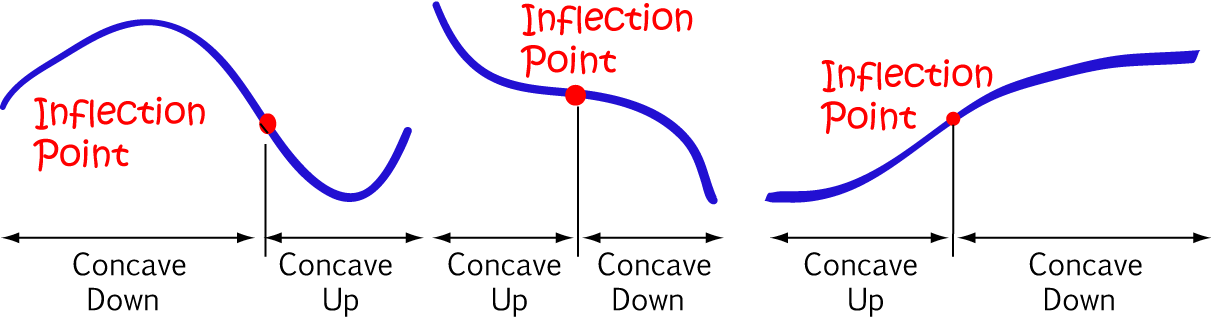
Use Calculus

You guessed it! Calculus is the best tool we have available to help us find points of inflection. Derivatives are what we need.

Remember, we can use the first derivative to find the slope of a function. However, we want to find out when the slope is increasing or decreasing, so we need to use the second derivative.

• If a function is concave up, then its second derivative is positive.
• If a function is concave down, then its second derivative is negative.
• What if the second derivative is zero? There might just be a point of inflection.

Note: You have to be careful when the second derivative is zero. Sometimes this can happen even if there's no point of inflection. For example, the second derivative of the function \(y = 17\) is always zero, but the graph of this function is just a horizontal line, which never changes concavity.

For there to be a point of inflection at \((x_0,y_0)\), the function has to change concavity from concave up to concave down (or vice versa) on either side of \((x_0,y_0)\).

Example

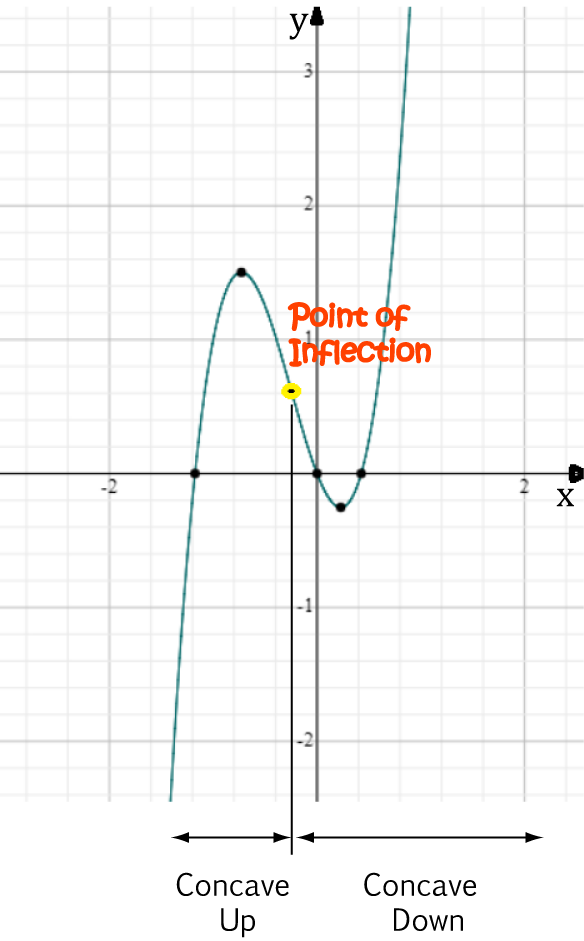
Find the points of inflection of \(y = 4x^3 + 3x^2 - 2x\).

Start by finding the second derivative:

• \(y' = 12x^2 + 6x - 2\)
• \(y'' = 24x + 6\)

Now, if there's a point of inflection, it will be a solution of \(y'' = 0\). In other words,

Before we can be sure we have a point of inflection, we need to check whether there's a change in concavity:

• For \(x
• For \(x > -\dfrac{1}{4}\), \(24x + 6 > 0\), so the function is concave up.

It looks like we have a point of inflection at \(x = -\dfrac{1}{4}\). The \(y\)-value is \(\dfrac{5}{8}\), so the co-ordinates of the point of inflection are \(\left(-\dfrac{1}{4}, \dfrac{5}{8} \right)\).

Quick Review of Derivatives

Just how did we find the derivative in the above example? There are a number of rules that you can follow to find derivatives. We used the power rule to find the derivatives of each part of the equation for \(y\), and then added them together

• The derivative of \(x^3\) is \(3x^2\), so the derivative of \(4x^3\) is \(4(3x^2) = 12x^2\)
• The derivative of \(x^2\) is \(2x\), so the derivative of \(3x^2\) is \(3(2x) = 6x\)
• Finally, the derivative of \(x\) is \(1\), so the derivative of \(-2x\) is \(-2(1) = -2\)

Adding them all together gives the derivative of \(y\): \(y' = 12x^2 + 6x - 2\).

Next, we differentiated the equation for \(y'\) to find the second derivative \(y'' = 24x + 6\).

Let's try one more example:

Example

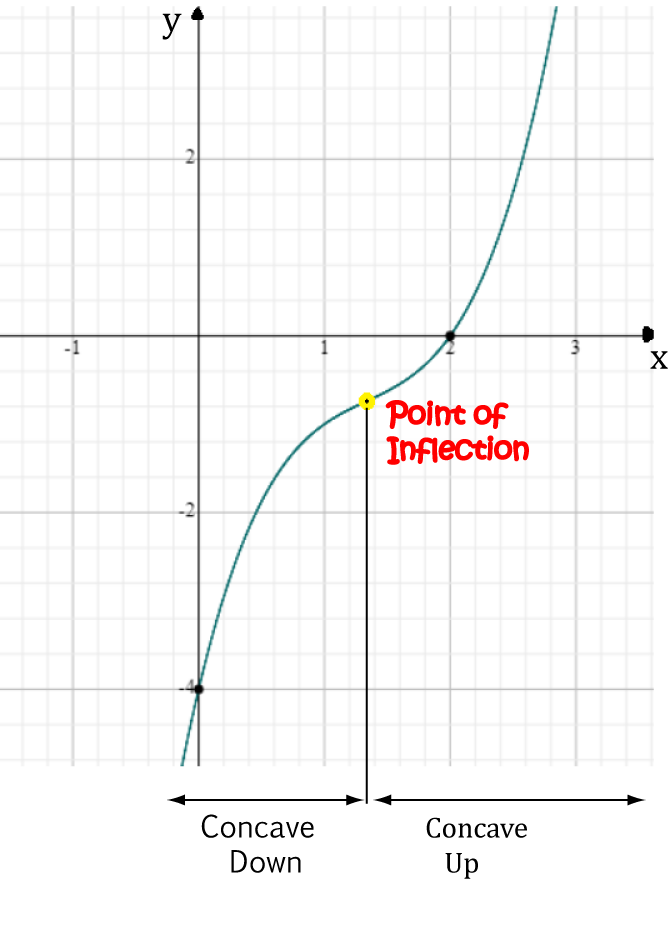
Find the points of inflection of \(y = x^3 - 4x^2 + 6x - 4\).

Start by finding the second derivative:

• \(y' = 3x^2 - 8x + 6 \)
• \(y'' = 6x - 8\)

Now, if there's a point of inflection, it will be a solution of \(y'' = 0\). In other words,

Before we can be sure we have a point of inflection, we need to check whether there's a change in concavity:

• For \(x
• For \(x > \dfrac{4}{3}\), \(6x - 8 > 0\), so the function is concave up.

It looks like we have a point of inflection at \(x = \dfrac{4}{3}\). The \(y\)-value is \(-\dfrac{20}{27}\), so the co-ordinates of the point of inflection are \(\left(\dfrac{4}{3}, -\dfrac{20}{27} \right)\).