Reading:

Calculus

Chapters

How Do We Find Integrals of Products?

We've seen that we have to be careful when taking derivatives of products: you can't just take the product of the derivatives. You have to use the product rule instead:

\(\dfrac{d}{dx}(uv) = uv' + vu'\).

So, it stands to reason that when we want to find the integral of a product of functions, we can't just take the product of the integrals. We have to get a bit cleverer and 'undo the product rule':

\( \begin{align*} \int \dfrac{d}{dx}(uv) \; dx &= \int uv'\;dx + \int vu'\; dx\\ uv &= \int uv'\; dx + \int vu'\;dx\\ \int uv'\; dx &= uv - \int vu'\;dx. \end{align*} \)

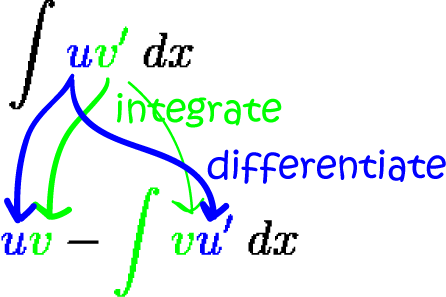
The last line is the integration by parts formula:

\(\displaystyle{\int uv'\;dx = uv - \int vu'\; dx.}\)

Integration by parts (or simply 'parts' for short) is often used to find the integrals of products of functions. Note that \(u\) and \(v\) are both functions. We need to choose one function to integrate and another one to differentiate as indicated in the diagram below:

Let's try a couple of examples.

Example 1

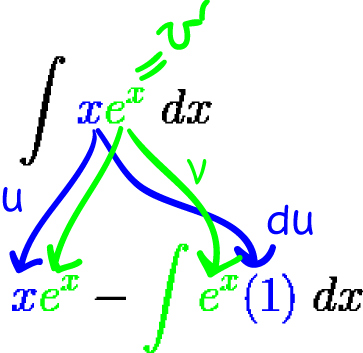
Find \(\displaystyle{\int xe^x \;dx}\)

First, we need to choose one function to differentiate (\(u\)) and another one to integrate (\(v'\)).

Let's try setting \(u = x\) and \(v' = e^x\)

Now our integral is in the form

\(\displaystyle{\int uv'\;dx }\)

and we can apply the integration by parts formula to integrate it.

Differentiate \(u\): \(u' = 1\)
Integrate \(v'\): \(v = \displaystyle{\int e^x\; dx} = e^x\)

Now plug everything into the formula to find the integral:

Finally, simplify to give:

\( \begin{align*} \displaystyle{\int xe^x\;dx } &= xe^x - \int e^x \; dx\\ &= xe^x - e^x + C. \end{align*} \)

Here are the steps we followed:

Choose \(u\) and \(v'\) (one to differentiate and the other to integrate)
Differentiate \(u\) to give \(u'\)
Integrate \(v'\) to give \(v\)
Plug them into the formula: \(\displaystyle{\int uv'\;dx = uv - \int vu'\; dx.}\)
Simplify and integrate.

Let's try some more examples.

Example 2

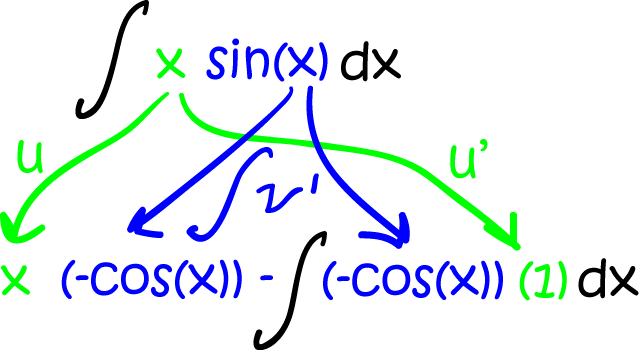
Find \(\displaystyle{\int x\sin x \;dx}\)

First we need to choose one function to differentiate (\(u\)) and another one to integrate (\(v'\)).

Let's try setting \(u = x\) and \(v' = \sin x\)

Now our integral is in the form

\(\displaystyle{\int uv'\;dx }\)

and we can apply the formula to integrate it.

Differentiate \(u\): \(u' = 1\)
Integrate \(v'\): \(v = \int \sin x\; dx = - \cos x\)

Now plug everything into the formula to find the integral:

Finally, simplify to give:

\( \begin{align*} \displaystyle{\int x\sin x\;dx } &= x(-\cos x) - \int (-\cos x) \; dx\\ &= -x \cos x + \int \cos x \; dx\\ &= -x\cos x + \sin x + C. \end{align*} \)

Choosing \(u\) and \(v'\)

You might have noticed in the last two examples that the expressions we chose for \(u\) and \(v'\) actually made the integral simpler once we'd applied the integration by parts formula. Most of the time, this is exactly what we try to do: make our lives easier. We try choose a function for \(u\) that will get simpler as we differentiate it, and a function for \(v'\) that is easy to integrate.

Let's have a look at how things can go horribly wrong if we choose \(u\) and \(v'\) badly.

Example 3

What is \(\displaystyle{\int x\cos (x) \;dx}\)

First, we need to choose one function to differentiate (\(u\)) and another one to integrate (\(v'\)).

Let's try setting \(u = \cos (x)\) and \(v' = x\)

Now our integral is in the form

\(\displaystyle{\int uv'\;dx }\)

and we can apply the formula to integrate it.

Differentiate \(u\): \(u' = -\sin (x)\)
Integrate \(v'\): \(v = \displaystyle{\int x\; dx }= \dfrac{x^2}{2}\)

Now plug everything into the formula to find the integral:

\( \begin{align*} \displaystyle{\int x\cos(x)\;dx } &= \dfrac{x^2}{2}(\cos(x)) - \int \dfrac{x^2}{2}(- \sin (x)) \; dx\\ &= \dfrac{x^2 \cos (x)}{2} + \int \dfrac{x^2}{2}\; \sin (x) \; dx \end{align*} \)

But this doesn't help us! It's even more complicated than before. So, it's really important to make good choices of \(u\) and \(v'\)

Let's try doing it the right way: set \(u = x\) and \(v' = \cos x\).

Differentiate \(u\): \(u' = 1\)
Integrate \(v'\): \(v = \int \cos(x)\; dx = \sin x\)

Now plug everything into the formula to find the integral:

\( \begin{align*} \int x \cos (x)\;dx &= x \sin (x) - \int \sin (x)(1)\;dx\\ &= x \sin (x) - \int \sin(x)\; dx\\ &= x \sin (x) - (- \cos(x)) + C\\ &= x \sin (x) + \cos (x) + C\\ \end{align*}\)

That's much better!

So, most of the time, we need to choose a \(u\) that gets simpler when you differentiate it, and a \(v'\) that is easy to integrate, or at least doesn't become any more complicated when you integrate it. Sometimes, however, we need to use some cunning tricks! Let's look at an example.

Example 4

Find \(\displaystyle{\int \ln(x)\;dx}\)

At first glance, this doesn't even look like there's a product anywhere in sight. But there's a \(1\) hiding:

\(\displaystyle{\int \ln (x)\; dx = \int 1 \cdot \ln(x)\;dx}\)

And now for the integration party-trick! Choose your values of \(u\) and \(v'\). The \(v'\) we want here actually gets more complicated as we integrate it, but that's OK because choosing \(u = \ln(x)\) will get us out of trouble. So, set \(v' = 1\) (that's right!) and \(u = \ln (x) \). Then

Differentiate \(u\): \(u' = \dfrac{1}{x}\)
Integrate \(v'\): \(v = \displaystyle{ \int (1)\; dx} = x\)

Now apply the formula and simplify to give:

\(\begin{align*} \int \ln (x)\; dx &= x \ln (x) - \int \left(\dfrac{1}{x}\right)(x)\;dx\\ &= x \ln (x) - \int \; dx\\ &= x \ln (x) - x + C \end{align*} \)

Clever, isn't it?

Using Integration by Parts More Than Once

If our integrand (the thing we're integrating) involves a power of \(x\) such as \(x^2\) or \(x^3\), we might need to use integration by parts more than once to evaluate our integral. Remember, make sure all your \(u\)s and \(v'\)s come from the same place. If you start interchanging them, you'll start going around in circles.

Example 5

Find \(\displaystyle{\int x^2 e^x \; dx}\)

We want our \(u\)s to get simpler as we differentiate them, and our \(v'\)s not to get any more complicated, so we choose \(u = x^2\) and \(v' = e^x\). Next,

Differentiate \(u\): \(u' = 2x\)
Integrate \(v'\): \(v = \displaystyle{\int e^x\; dx} = e^x\)

and apply the integration by parts formula to give:

\(\begin{align*} \int x^2 e^x\; dx &= x^2e^x - \int e^x (2x)\;dx\\ &= x^2e^x - 2\int xe^x \; dx \end{align*} \)

But now we have another product to integrate! Not to worry, it's simpler than the last one, so we can just use parts again. Remember, we need to keep the \(u\)s and \(v'\)s coming from the same place, so we set \(u = x\) and \(v' = e^x\). Then

Differentiate \(u\): \(u' = 1\)
Integrate \(v'\): \(v = \int e^x\; dx = e^x\)

and apply the formula AGAIN to find

\( \begin{align*} \displaystyle{\int xe^x\;dx } &= xe^x - \int e^x \; dx\\ &= xe^x - e^x + C. \end{align*} \)

Now, stitch it all together to give

\( \begin{align*} \displaystyle{\int x^2e^x\;dx } &= x^2e^x - 2\int xe^x \; dx\\ &= x^2 e^x - 2 \left[ xe^x - e^x + C\right]\\ &= x^2 e^x - 2xe^x + 2e^x + C' \end{align*} \)

One Last Integration Party Trick (sometimes it's OK to go around in circles)

Let's try to find \(\displaystyle{\int e^x \cos(x) \; dx}\)

It's a product, so integration by parts sounds like a good idea. Choose your weapons:

Set \(u = \cos(x)\)
Set \(v' = e^x\)

Then

Differentiate \(u\): \(u' = -\sin (x)\)
Integrate \(v'\): \(v = \displaystyle{\int e^x\; dx} = e^x\)

and apply the integration by parts formula:

\( \begin{align*} \displaystyle{\int e^x \cos(x) \;dx } &= e^x\cos(x) - \int e^x (-\sin (x)) \; dx\\ &= e^x \cos (x) + \int e^x \sin (x) \;dx. \end{align*} \)

But this doesn't look any simpler! Don't panic! The derivatives of \(\cos(x)\) and \(\sin (x)\) go around in a cycle. You can sometimes exploit this fact to calculate the integral. So, let's try integration by parts again. Remember to keep your \(u\)s and \(v'\)s coming from the same place. Set \(u = \sin (x)\) (\(u\) was \(\cos (x)\) in the last step), and \(v' = e^x\) as in the preceding step. Then

Differentiate \(u\): \(u' = \cos (x)\)
Integrate \(v'\): \(v = \displaystyle{\int e^x\; dx} = e^x\)

and apply the integration by parts formula again to give

\( \begin{align*} \displaystyle{\int e^x \cos(x) \;dx } &= e^x \cos (x) + \int e^x \sin (x) \;dx\\ &= e^x \cos(x) + (e^x \sin (x) - \int e^x \cos(x)\; dx) \end{align*} \)

Now, do you notice something? We have the same integral on both sides of the equation, except that it's subtracted from the right hand side and positive on the left hand side. Pull it over to the left!

\( \begin{align*} 2\displaystyle{\int e^x \cos(x) \;dx } &= e^x \cos(x) + e^x \sin (x) + C \end{align*} \)

Now, divide both sides by \(2\):

\( \begin{align*} \displaystyle{\int e^x \cos(x) \;dx } &= \frac{e^x \cos(x) + e^x \sin (x) + C}{2} \end{align*} \)

and we're done! That one was pretty tricky, huh?

Now's the time to get plenty of practice. Don't worry, it takes a bit of getting used to, but integration by parts will soon become your new best friend. Mathematics is definitely not a spectator sport!

Description

Calculus is the branch of mathematics that deals with the finding and properties of derivatives and integrals of functions, by methods originally based on the summation of infinitesimal differences. The two main types are differential calculus and integral calculus.

Environment

It is considered a good practice to take notes and revise what you learnt and practice it.

Audience

Grade 9+ Students

Learning Objectives

Familiarize yourself with Calculus topics such as Limits, Functions, Differentiability etc

Author: Subject Coach
Added on: 23rd Nov 2017

You must be logged in as Student to ask a Question.

None just yet!

Calculus

Chapters

How Do We Find Integrals of Products?

How Do We Find Integrals of Products?

Example 1

Example 2

Choosing \(u\) and \(v'\)

Example 3

Example 4

Using Integration by Parts More Than Once

Example 5

One Last Integration Party Trick (sometimes it's OK to go around in circles)

Description

Environment

Audience

Learning Objectives

THANK YOU FOR STOPPING BY!