Calculus
Chapters
What are Derivatives?
What are Derivatives?
Derivatives quantify changes in functions. For example, you might want to measure the change in the time your parents spend nagging you to do your homework as you get older. This would be measured using the slope of the nagging duration function. Derivatives allow you to measure the rate of change of the duration of nagging at a particular instant in time.
Let's explore this idea a little further.
Introduction
Derivatives measure the slope of a function.
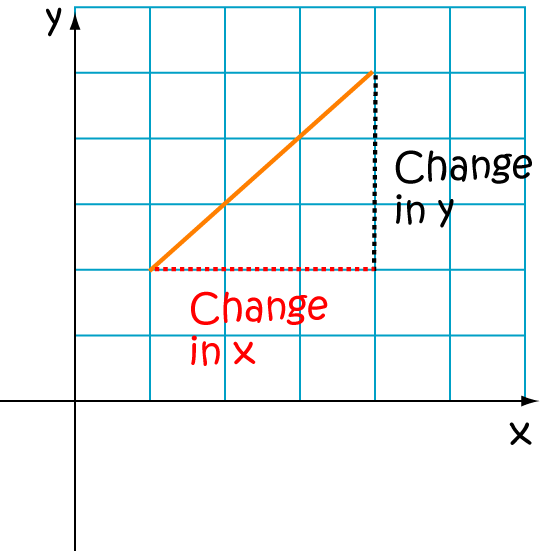
In the picture,
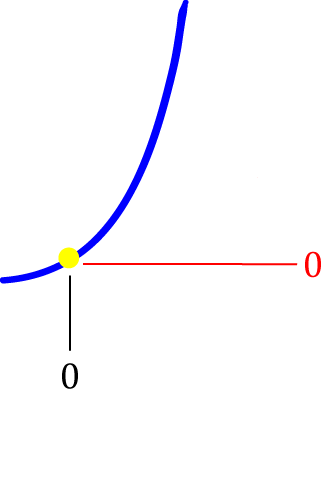
There's no change in \(x\) or \(y\) to measure!
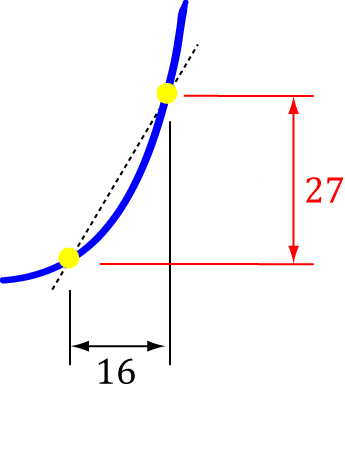
In the picture,
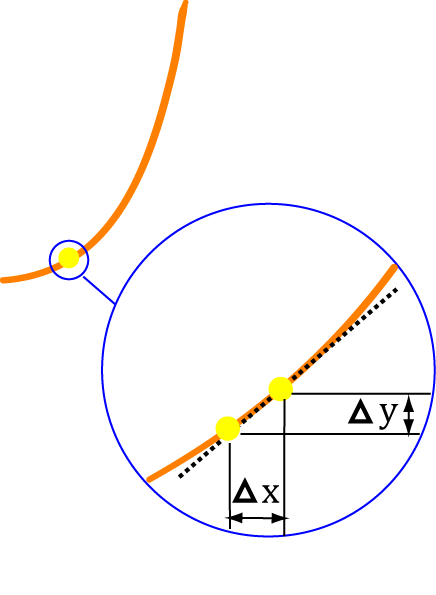
\(\dots\) and then we let our small difference become smaller and smaller. In other words, we let it approach zero.
Finding Derivatives
- \(x\) changes to \(x + \Delta x\)
- \(y = f(x)\) changes to \(f(x + \Delta x)\)
- Apply the slope formula: \(\dfrac{\Delta y}{\Delta x} = \dfrac{f(x + \Delta x) - f(x)}{\Delta x}\)
- Simplify it.
- Let \(\Delta x\) approach zero.

Example
Let's start with an easy example: the function \(f(x) = x + 3\)
\(f(x) = x + 3\) and \(f(x + \Delta x) = (x + \Delta x) + 3\).
Now the slope formula gives \(\dfrac{f(x + \Delta x) - f(x)}{\Delta x}\),
and plugging in our values for \(f(x + \Delta x)\) and \(f(x)\) gives \(\dfrac{(x + \Delta x) + 3 - (x + 3)}{\Delta x}\),
which simplifies to: \(\dfrac{x + \Delta x + 3 - x - 3}{\Delta x} = \dfrac{\Delta x}{\Delta x}\).
Dividing top and bottom by \(\Delta x\) yields \(\dfrac{1}{1} = 1\).
Letting \(\Delta x\) approach zero in this case does nothing, so the derivative of \(f(x) = x + 3\) is \(1\).
Notation: We write \(dx\) to mean \(\Delta x\) approaches \(0\) and \(\dfrac{d}{dx} (\text{something})\) to mean "the derivative of something". So, in the example, we have
A more complicated example
What is the derivative of the function \(f(x) = x^2 + 3x\)?
\(f(x) = x^2 + 3x\) and \(f(x + \Delta x) = (x + \Delta x)^2 + 3(x + \Delta x)\).
Expand \(f(x + \Delta x)\):
Now the slope formula gives \(\dfrac{f(x + \Delta x) - f(x)}{\Delta x}\),
and plugging in our values for \(f(x + \Delta x)\) and \(f(x)\) yields \(\dfrac{x^2 + x (2 \Delta x + 3) + 3 \Delta x + (\Delta x)^2 - (x^2 + 3x)}{\Delta x}\),
which simplifies to: \(\dfrac{x^2 + 2x\Delta x + 3x + 3 \Delta x + (\Delta x)^2 - x^2 - 3x}{\Delta x} = \dfrac{2x\Delta x + 3\Delta x + (\Delta x)^2}{\Delta x}\).
Dividing top and bottom by \(\Delta x\) yields \(\dfrac{2x + 3 + \Delta x}{\Delta x} = 2x + 3 + \Delta x\).
Letting \(\Delta x\) approach zero gives \(2x + 3\), so \(f'(x) = 2x + 3\).
Finding derivatives of other functions
You can use this "definition of the derivative" approach to find the derivative of any function you like, but it can become rather tedious. It is more usual (and more efficient) to use the rules of derivatives to calculate more complicated derivatives.
Example:
What is the derivative of \(\tan (x)\)?
You could work this out as above, but you'll need to do a fair bit of algebra, and use some trigonometric identities. Alternatively, you could take the easy (sensible) way out and use the rules of derivatives to tell you that
Note: You need to be careful when applying the rules of derivatives. For example, if someone asked you to find the derivative of
\(\text{Engelbert}(x)*\text{Filbert}(x)\), you
couldn't just multiply the two derivatives together. You'd have to use something called the product rule, which is described in
the article on the rules of derivatives.
Example:
What is the derivative of \(\cos^2(x)\)?
It absolutely isn't \(\left(\dfrac{d}{dx}(\cos (x)) \right)^2 = \sin^2 (x)\). If you look at the rules of derivatives article, it will tell you about something
called the chain rule (or function of a function rule) that is useful here. Using this rule gives \(\dfrac{d}{dx} (\cos^2 (x)) = -2\cos(x)\sin(x)\),
which is a teeny bit different from \(\sin^2 (x)\).
The next step is to learn all about the rules of derivatives.
Derivatives as Limits
The idea of \(\Delta x\) approaching zero is more precisely expressed using limit notation like this:
Description
Calculus is the branch of mathematics that deals with the finding and properties of derivatives and integrals of functions, by methods originally based on the summation of infinitesimal differences. The two main types are differential calculus and integral calculus.
Environment
It is considered a good practice to take notes and revise what you learnt and practice it.
Audience
Grade 9+ Students
Learning Objectives
Familiarize yourself with Calculus topics such as Limits, Functions, Differentiability etc
Author: Subject Coach
Added on: 23rd Nov 2017
You must be logged in as Student to ask a Question.
None just yet!