Arc Length of Curves

In this article we'll learn how to use calculus to find the lengths of curves. It would be a good idea to read the articles on derivatives and integrals before trying to tackle the material in this article.

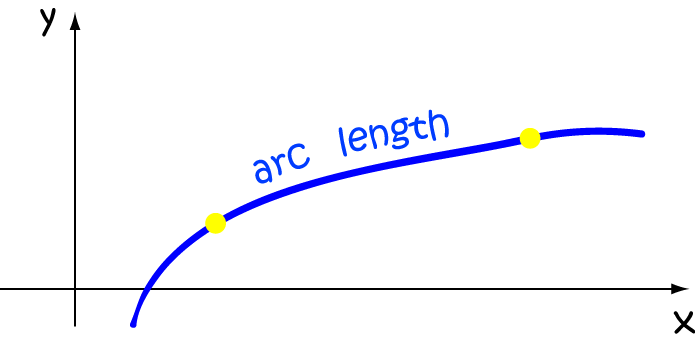
To find the length of a smooth curve (this means the derivative has to be continuous) joining two points as in the diagram above, we begin by breaking the curve up into small chunks. We then use the distance formula to find an approximation for the length of each of these chunks:

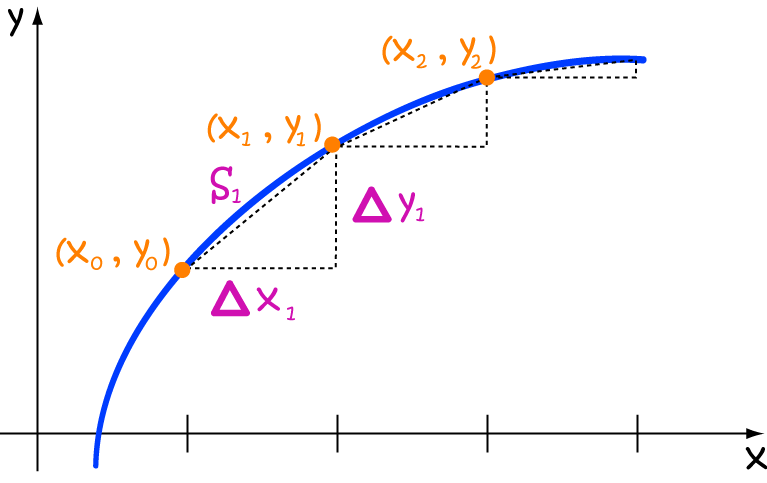
• The distance between \(x_0\) and \(x_1\) is given by:
  \(S_1 = \sqrt{(x_1 - x_0)^2 + (y_1 - y_0)^2} \)
• Now suppose the difference between \(x_0\) and \(x_1\) is really really small. Call it \(\Delta x_1\). Similarly, call the difference between \(y_0\) and \(y_1\) \(\Delta y_1\):
  \(S_1 = \sqrt{(\Delta x_1 )^2 + (\Delta y_1 )^2}\)
• Repeat this calculation for all the points along the curve:
  \( \begin{align*} S_2 &= \sqrt{(\Delta x_2 )^2 + (\Delta y_2 )^2}\\ S_3 &= \sqrt{(\Delta x_3 )^2 + (\Delta y_3 )^2}\\ \dots\\ S_n &= \sqrt{(\Delta x_n )^2 + (\Delta y_n )^2} \end{align*} \)
• We can use summation notation to summarise all of the above lines into one line:
  \(S \approx \displaystyle{\sum_{i=1}^n \sqrt{(\Delta x_i)^2 + (\Delta y_i)^2} }\)

Let's go through a sequence of steps that will help us to turn our nasty looking sum into a nice, friendly integral. The first thing to do is make all the \(\Delta x_i\)s the same size, say \(\Delta x\). Later we'll be able to pull them out from under the square root, but we'll have to indulge in some underhanded algebraic tricks first. Let's get to work:

Start by dividing and multiplying each \(\Delta y_i\) by \(\Delta x\) (have you ever seen anything so devious?). This gives:

Next, factor out that \((\Delta x_i)^2\) under the square root:

It's time to pull that \((\Delta x_i)^2\) out from under the square root:

Now, we let \(n\) tend to \(\infty\). This means that there are more slices, so that each slice (and hence, each \(\Delta x_i\)) will get smaller:

This infinite sum is actually an integral, and we write \(dx\) for the small slices \(\Delta x\) of \(x\) that we get in the limit. Our \(\Delta y_i\)s are also getting smaller, so we write them as \(dy\):

Of course, we can also write \(f'(x) = \dfrac{dy}{dx}\), so we have derived the arc length formula:

This doesn't involve anywhere near as many calculations!

Note: If you know \(x = g(y)\), where \(g(y)\) is a continuously differtiable function of \(y\), you can also calculate the arc-length using the formula:

Let's work on some simple examples so that we become familiar with the formula.

Example

Find the arc-length of the curve \(f(x) = 1\) between \(x = 2\) and \(x = 4\).

As \(f(x) = 1\) is just a constant function (horizontal line), \(f'(x) = 0\). So, we can use the formula to calculate:

\(\begin{align*} S &= \int_2^4 \sqrt{1 + (f'(x))^2}\;dx\\ &= \int_2^4 \sqrt{1 + (0)^2}\; dx\\ &= \int_2^4 \; dx\\ &= \left[x \right]^4_2\\ &= 4 - 2 = 2. \end{align*} \)

So, the length of the arc between \(2\) and \(4\) is \(2\). We can, of course, verify this by looking at the graph.

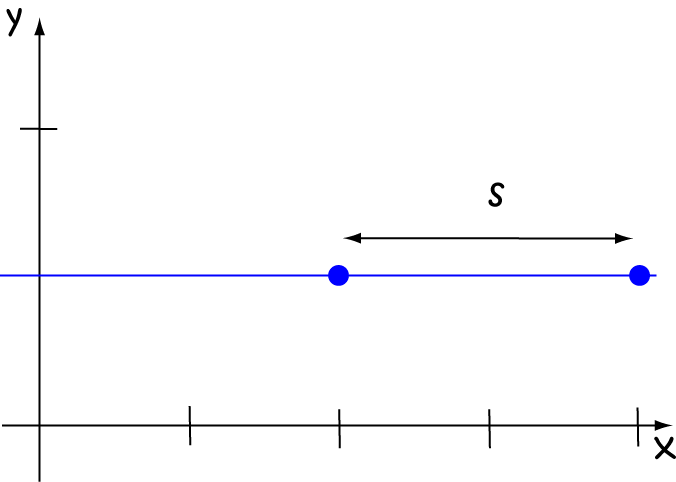
Note: The expression \(\sqrt{1 + (f'(x))^2}\) in the integrand of the arc length formula guarantees that the arc length will be at least the distance between the \(x\)-values at the end points of our interval.

Example

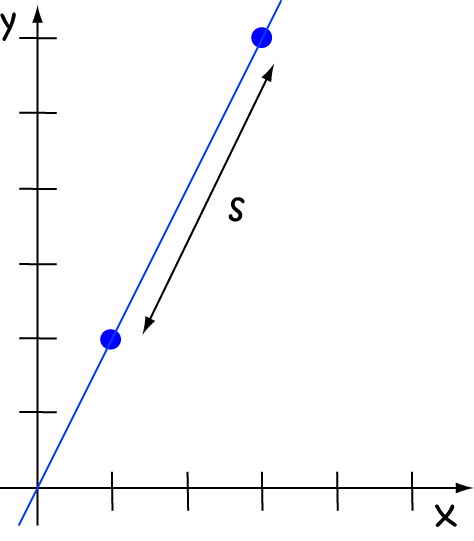
Find the arc-length of the curve \(f(x) = 2x\) between \(x = 1\) and \(x = 3\).

As \(f(x) = 2x\) is just a straight-line function, \(f'(x) = 2\). So, we can use the formula to calculate:

\(\begin{align*} S &= \int_1^3 \sqrt{1 + (f'(x))^2}\;dx\\ &= \int_1^3 \sqrt{1 + (2)^2}\; dx\\ &= \int_1^3 \sqrt{5} \; dx\\ &= \left[\sqrt{5}x \right]^3_1\\ &= \sqrt{5}(3 - 1)\\ &= 2 \sqrt{5} \end{align*} \)

Now let's set to work on a real-world example. This one is slightly harder.

Example

Cuthbert the crab has hurt his leg and can't scuttle as effectively as usual. He decides to build a suspension bridge joining one rock pool to another that is 15 cm away. He needs to know the required length of a bridge that joins the two rocks, and follows the curve:

Note: This kind of curve is called a catenary. It is the shape formed by all hanging suspension bridges like the one in the photo. The general form for this type of curve is

Cuthbert's bridge will look like the one in the picture below, but on a smaller scale:

and the curve required looks like this:

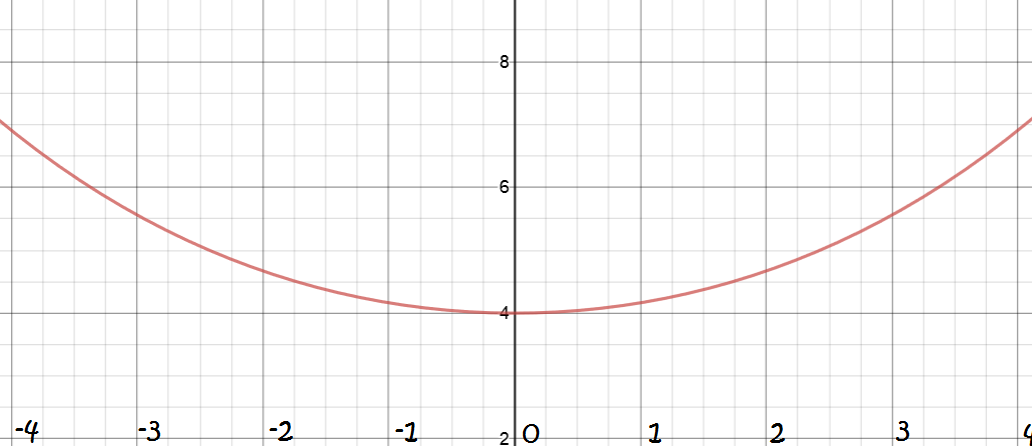
Let's find the arc-length of the curve. Because the curve is symmetric, we can just work with half of it and double our answer. We first calculate

Now to find the arc length:

Note: Seriously, though, these bridges are quite commonly built on a larger scale to Cuthbert's. So, this example is important. Their arc length must always be greater than the distance they need to span, and is always given by the formula:

There's time for one last example.

Example

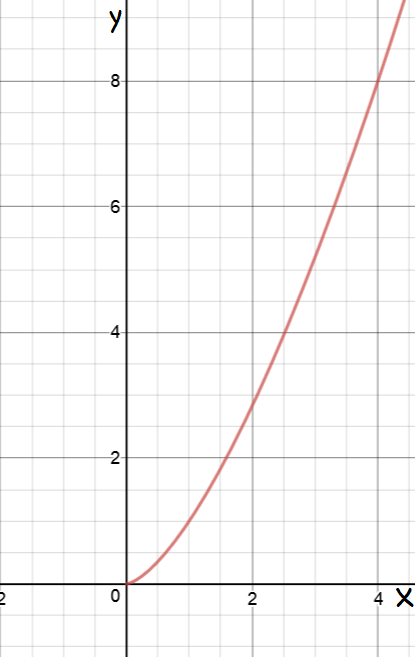
Find the arc-length of the curve \(f(x) = x^{\frac{3}{2}}\) between \(x = 0\) and \(x = 2\).

By the power rule, the derivative of \(f(x) = x^{\frac{3}{2}}\) is \(f'(x) = \dfrac{3}{2} x^{\frac{1}{2}}\). So, we can use the formula to calculate:

\(\begin{align*} S &= \int_0^2 \sqrt{1 + (f'(x))^2}\;dx\\ &= \int_0^2 \sqrt{1 + \left( \dfrac{3}{2} x^{\frac{1}{2}}\right)^2}\; dx\\ &= \int_0^2 \sqrt{1 + \dfrac{9}{4}\;x} \; dx\\ \end{align*} \)

Now use integration by substitution. Set \(u = 1 + \dfrac{9}{4}\;x\). Then \(du = \dfrac{9}{4} dx\), so \(\dfrac{4}{9} du = dx\). Next, we need to change the limits. When \(x = 0\), \(u = 1\), and when \(x = 2\), \(u = 1 + \dfrac{9}{4}(2) = \dfrac{11}{2}\). So,

\(\begin{align*} S &= \int_1^{\frac{11}{2}} \dfrac{4}{9} \sqrt{u} \; du\\ &= \left[ \left( \frac{4}{9}\right) \left(\frac{2}{3}\right) u^{\frac{3}{2}}\right]^{\frac{11}{2}}_1\\ &= \dfrac{8}{27} \left( \left( \dfrac{11}{2}\right)^{\frac{3}{2}} - 1 \right) \approx 3.526\\ \end{align*} \)

Things to Remember

• The arc length formula for the function \(f(x)\) is given by the integral
  \(S = \displaystyle{\int^b_a \sqrt{1 + \left(f'(x)\right)^2}\; dx}\)
• The arc length is always as least as long as the distance between the two end points of the arc.