Reading:

Calculus

Chapters

Finding Areas Between Curves

Why would anyone want to find the areas between curves? I'm glad you asked.

Here's a very important real-world application of this process.

Finding Areas Between Curves

Remember Gus the snail? He's in training to beat the world land-speed record. In the article introducing integration, we talked about Gus' velocity curve, and how he wanted to know the total distance he'd covered during training sessions. By taking a definite integral, we found that his total distance covered (or the area under his velocity curve) was \(75 \text{ nm}\). However, it turns out that Gus didn't realise he was practising on top of a skateboard. The skateboard was moving very slowly, but it was, nonetheless, moving. So now Gus wants to know how much of that distance was him, and how much was the skateboard. The two velocity curves are shown in the picture below.

Gus' contribution to the total distance covered is the area between the two velocity curves. If the total distance covered by the skateboard during the \(4\) seconds was \(15 \text{ nm}\), then Gus' contribution was \(75 - 15 = 60\text{ nm}\). So the area between the two curves is \(60 \) square units.

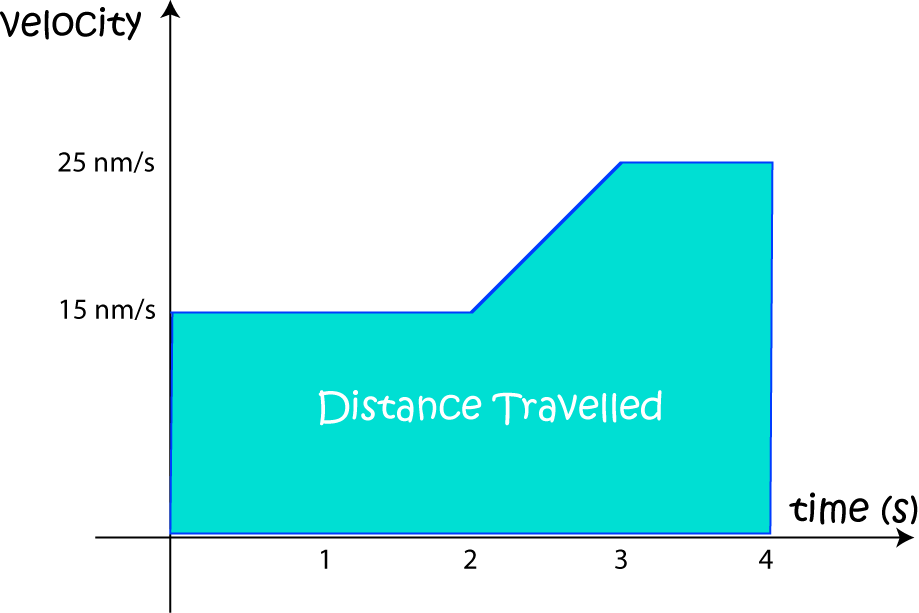
Writing this all down using integral notation, we have

\( \displaystyle{\int^4_0 \text{velocity}(t)\; dt - \int^4_0\text{skateboard}(t)\; dt = \int^4_0 (\text{velocity}(t) - \text{skateboard}(t)) \; dt = 60 \text{ nm} }\)

Did you notice that we put Gus' velocity curve first? That's because it's the curve on top.

Let's explore the techniques for finding areas between curves in a little more depth.

Finding Areas between Curves

Because the \(xy\)-plane has two different axes, there are two different ways we can calculate the area between two curves: either in the \(x\)-direction or in the \(y\)-direction. The option you choose will depend on which one is easier to integrate, or has the fewest complications.

If we want to find the integral between the curves for \(y = f(x)\) and \(y = g(x)\) on the interval \([a,b]\), the first step is to work out which of \(f(x)\) and \(g(x)\) is on top. Let's assume that \(f(x)\) is the bigger one. This will mean that \(f(x) \geq g(x)\) for all \(x\) in the interval \([a,b]\) as shown in the diagram below:
The area will then be given by the integral
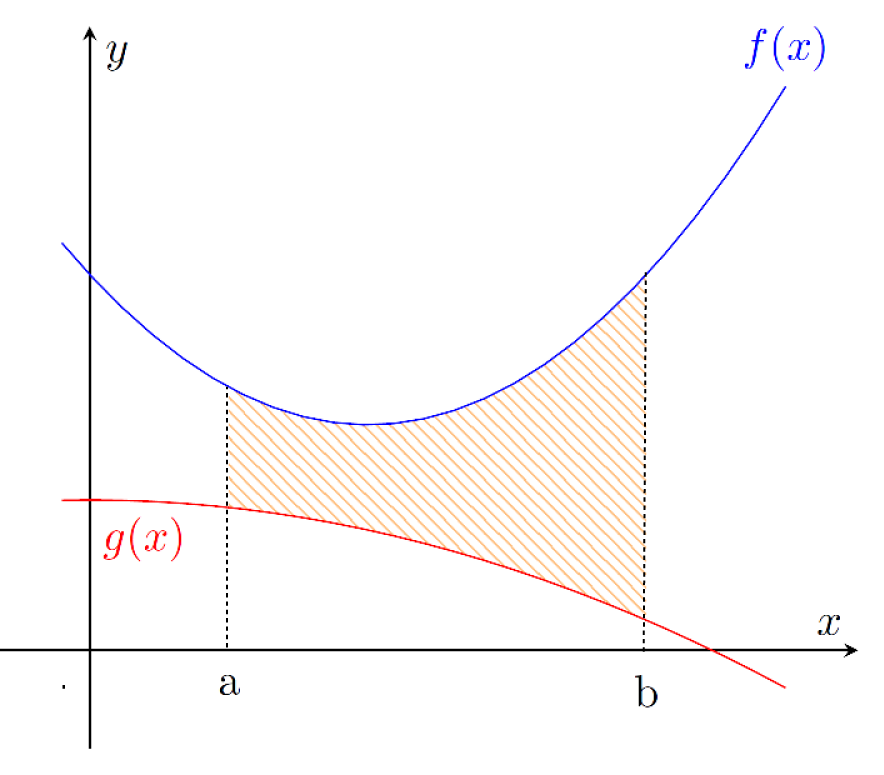\( \text{Area Between Curves} = \displaystyle{\int_a^b f(x) - g(x)\; dx} \)
If we want to find the integral between the curves for \(x = f(y)\) and \(x = g(y)\) on the interval \([c,d]\), the first step is to work out which of \(f(y)\) and \(g(y)\) is on the right. Let's assume that \(f(x)\) is the bigger one. This will mean that \(f(y) \geq g(y)\) for all \(y\) in the interval \([c,d]\) as shown in the diagram below:
The area will then be given by the integral
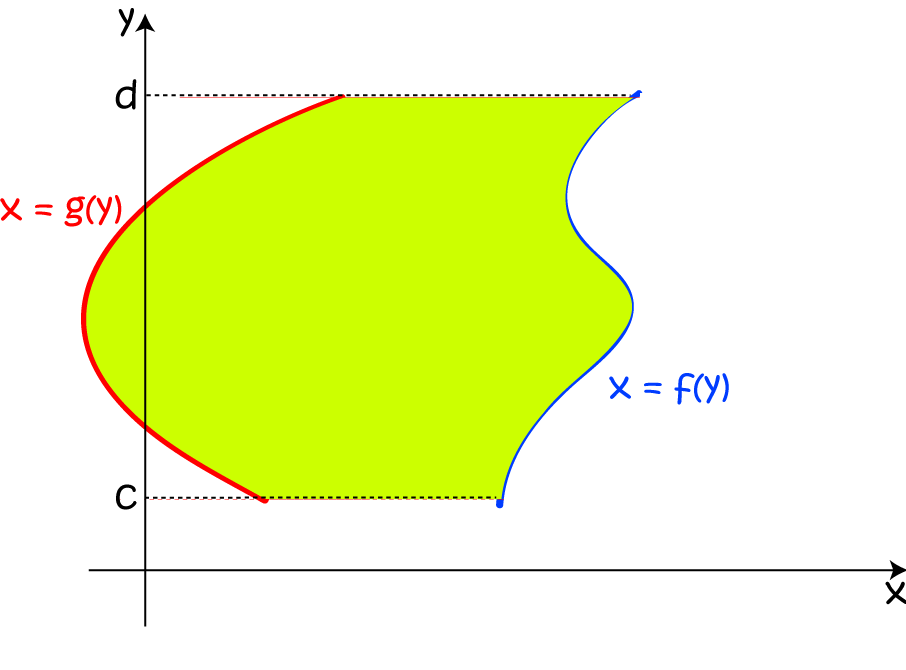\( \text{Area Between Curves} = \displaystyle{\int_c^d f(y) - g(y)\; dy} \)

We used the first formula to find Gus' total distance travelled during his world land-speed record training sessions above.

If you're anything like me, you'll find it easier to remember formulas that are written in words, rather than symbols. If not, then feel free to ignore the following few lines.

So, how would we say this in words?

To find the area between \(f(x)\) and \(g(x)\) over the interval \([a,b]\), take the integral of the upper function minus the lower function.
To find the area between \(f(y)\) and \(g(y)\) over the interval \([c,d]\), take the integral of the function to the right minus the function to the left.

Think about it: the area between the two curves is equal to the area under the top function minus the area that is under the bottom function. There... the people who don't like words can start paying attention again. We have two brand-spanking new formulas. Aren't you just itching to try them? I know I am. Let's finish this article off with a few examples.

Applying the Area Formulas

Example 1

Find the area of the region enclosed by the curves \(y = x^3\) and \(y = \sqrt{x}\).

First, note that we say that a region is "enclosed" by a set of curves if each of its boundaries is formed by one of the curves from the set. Let's have a look at a picture:

Now, the curve \(y = \sqrt{x}\) lies above the curve \(y = x^3\) throughout the region. We need to find the end points for the integration. These will be the points of intersection of the two curves. Set the equations of the two curves equal, and solve for \(x\). Note that \(x \geq 0\) throughout this region.

\( \begin{align*} \sqrt{x} &= x^3\\ x &= x^6 \;\;\;\;\;\;\;\;\;\;\text{squaring both sides}\\ x^6 - x &= 0\\ x(x^5 - 1) &= 0\\ x&=0 \text{ or }x = 1 \end{align*} \)

Now we're all set to find the area. Remember that we don't need to include the constant of integration for definite integrals. Using the power rule, we obtain:

\( \begin{align*} A &= \int_0^1 \text{upper} - \text{lower}\; dx\\ &= \int_0^1 \sqrt{x} - x^3 \; dx\\ &= \int_0^1 x^{\frac{1}{2}} - x^3 \; dx\\ &= \left[ \dfrac{2}{3}x^{\frac{3}{2}} - \dfrac{x^4}{4}\right]_0^1\\ &= \left( \dfrac{2}{3}(1) - \dfrac{1}{4} \right) - (0)\\ &= \dfrac{5}{12} \text{ square units}. \end{align*} \)

Steps for finding areas between curves

Draw the two graphs.
Decide which is upper and which is lower (or which is furthest to the right and furthest to the left)
Decide which formula to use.
Determine the limits of integration. These may be given, or they may need to be found using the points of intersection of the two curves.
Apply the formula to calculate the area.

Note: The answer should always be positive. If you get a negative answer, you have the curves around the wrong way.

Example 2

Find the area of the region bounded by the curves \(y = x+2\), \(y = \sin x\), \(x = 2\) and the \(y\)-axis.

First, note that the \(y\)-axis is the line \(x = 0\), so the last two bounds give you the limits of integration. Next, let's sketch the graph so we can decide which is the uppermost curve:

It looks like it's \(y = x + 2\). Since we already have the limits of integration, there's nothing to do except apply the formula to calculate the area. We'll need to use the power rule and the fact that \(\displaystyle{\int (-\sin (x))\; dx = \cos(x) + C}\).

\( \begin{align*} A &= \int_0^2 \text{upper} - \text{lower}\; dx\\ &= \int_0^2 (x + 2) - \sin(x) \; dx\\ &= \left[\dfrac{x^2}{2} + 2x + \cos (x)\right]_0^2\\ &= \left(\dfrac{4}{2} + 2(2) + \cos(2) \right) - (0 +\cos(0))\\ &= 6 + \cos(2) - 1\\ &= 5 + \cos(2)\\ &\approx 4.584 \text{ square units}. \end{align*} \)

Let's move on to our next example

Example 3

Find the area of the region bounded by the curves \(y = 2x^2 + 3\) and \(y = 4x + 9\).

Let's start by sketching the graphs so we can decide which is the uppermost curve:

It looks like it's \(y = 4x + 9\). Next, we need to find the limits of integration. They aren't obvious from the graph. Set the two equations equal to each other and solve for \(x\):

\( \begin{align*} 4x + 9 &= 2x^2 + 3\\ 4x + 6 &= 2x^2\\ 0 &= 2x^2 - 4x - 6\\ 0 &= x^2 - 2x - 3\\ 0 &= (x - 3)(x + 1). \end{align*} \)

So, the points of intersection occur at \(x = -1\) and \(x = 3\). These will be our limits of integration. Now, we can use the power rule, and sum and difference rules to calculate the enclosed area:

\( \begin{align*} A &= \int_{-1}^3 \text{upper} - \text{lower}\; dx\\ &= \int_{-1}^3 (4x +9) - (2x^2 + 3) \; dx\\ &= \int_{-1}^3 (-2x^2 + 4x + 6)\; dx\\ &= \left[-\dfrac{2x^3}{3} + 2x^2 + 6x\right]_{-1}^3\\ &= \left(-\dfrac{2(3)^3}{3} + 2(3)^2 + 6(2)\right) - \left(-\dfrac{2(-1)^3}{3} + 2(-1)^2 + 6(-1)\right)\\ &= \dfrac{64}{3} \text{ square units}. \end{align*} \)

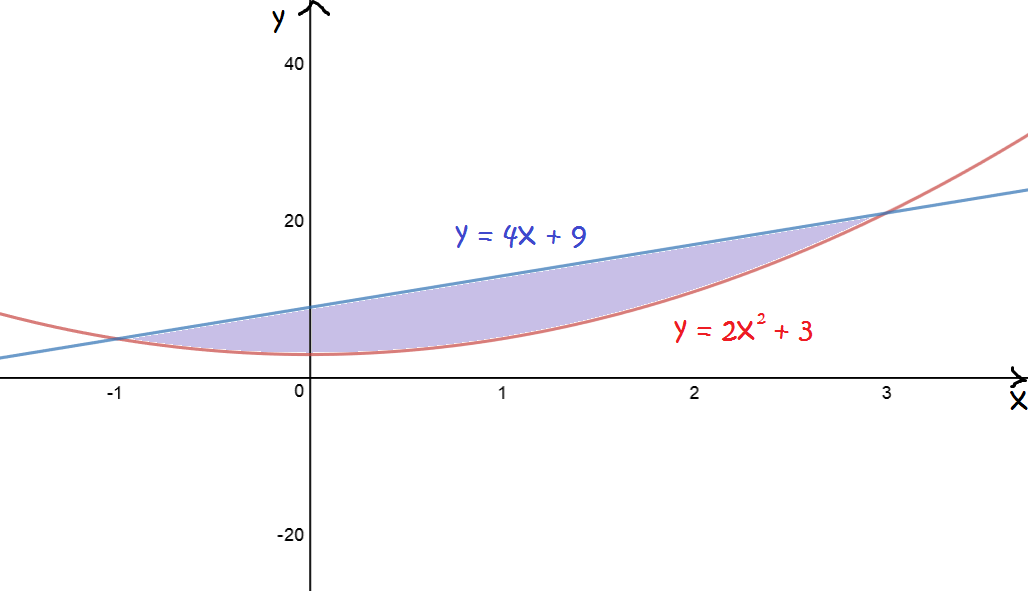
Now let's try a slightly trickier one.

Example 4

Find the area of the region enclosed by the curves \(y = 2\sin (x) \), \(y = 2 \cos(x) \), the line \(x = \dfrac{\pi}{2}\) and the \(y\)-axis.

Let's start by sketching the graphs so we can decide which is the uppermost curve:

The upper most curve changes where the graphs cross over. This happens when \(2\sin (x) = 2\cos(x)\), or, in other words, at \(x = \dfrac{\pi}{4}\). It looks like we'll have to split this one into two integrals. In the first integral, with limits \(x = 0\) to \(x = \dfrac{\pi}{4}\), we'll have \(y = 2 \cos(x)\) as the uppermost curve. The second integral will have limits \(x = \dfrac{\pi}{4}\) to \(x = \dfrac{\pi}{2}\), and \(y = 2 \sin (x)\) as the uppermost curve. Let's get integrating:

\( \begin{align*} A &= \int_{0}^{\frac{\pi}{4}} \text{upper} - \text{lower}\; dx + \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \text{upper} - \text{lower} \; dx\\ &= \int_{0}^{\frac{\pi}{4}} 2 \cos(x) - 2 \sin (x) \; dx + \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} 2 \sin (x) - 2 \cos(x) \; dx\\ &= \left[2 \sin (x) + 2 \cos (x)\right]_{0}^{\frac{\pi}{4}} + \left[-2 \cos(x) - 2 \sin(x)\right]_{\frac{\pi}{4}}^{\frac{\pi}{2}}\\ &= (2 \sqrt{2} - 2) + (2 \sqrt{2} - 2)\\ &= 4\sqrt{2}- 4 \text{ square units}. \end{align*} \)

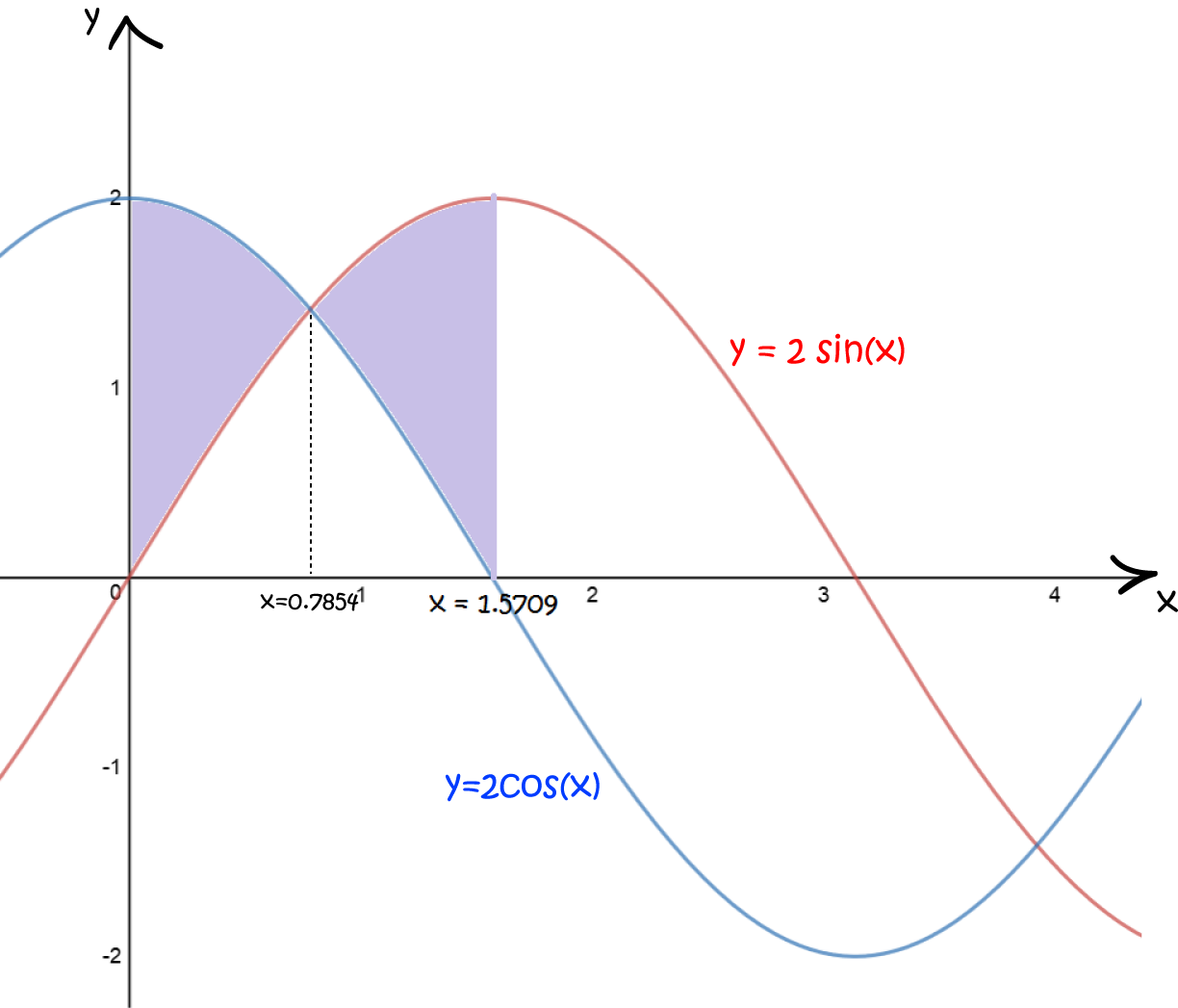
Now let's try an even trickier one.

Example 5

Find the area of the region enclosed by the curves \(x = y^2 - 1 \) and \(y = x - 1\).

There are two approaches we can use here. We can convert the equation \(x = y^2 - 1\) into the two equations \(y= \sqrt{x +1}\), and \(y = -\sqrt{x + 1}\) and apply the first formula, or we can convert the second equation \(y = x - 1\) into \(x = y + 1\) and apply the second formula for the area between the two curves. We'll start with the first approach, then try the second as well, so that we can compare our answers and decide which formula was easier to use to solve this problem.

Let's start by sketching the graphs so we can decide which is the uppermost curve:

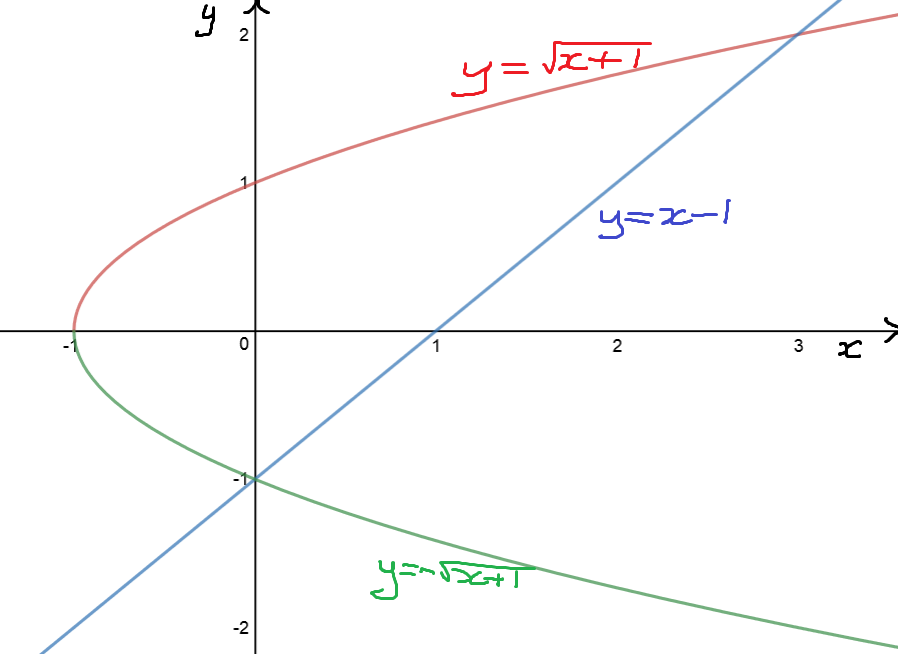
The graphs intersect at \(x = 0\) and \(x = 3\). The vertex of the parabola lies at \(x = -1\). Something peculiar is going on, however. If you split the region up along the \(y\)-axis, the region to the left has \(y = -\sqrt{x + 1}\) as the lower curve. To the right of the \(y\)-axis, \(y = x - 1\) is the lower curve. So, we'll need two integrals to find our area again.

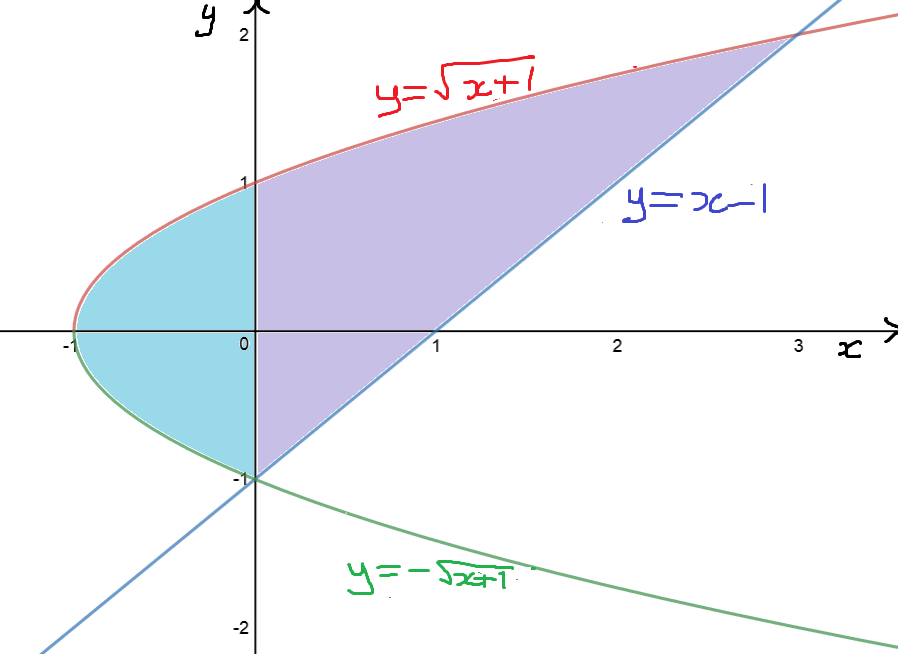
Let's hop to it:

\( \begin{align*} A &= \int_{-1}^{0} \text{upper} - \text{lower}\; dx + \int_{0}^{3} \text{upper} - \text{lower} \; dx\\ &= \int_{-1}^{0} \sqrt{x + 1} - (-\sqrt{x + 1}) \; dx + \int_{0}^{3} \sqrt{x + 1} - (x - 1) \; dx\\ &= \int_{-1}^{0} 2(x + 1)^{\frac{1}{2}} \; dx + \int_{0}^{3} \sqrt{x + 1} - (x - 1) \; dx\\ &= \left[\dfrac{4}{3}(x + 1)^{\frac{3}{2}}\right]_{-1}^{0} + \left[\dfrac{2}{3}(x + 1)^{\frac{3}{2}} -\dfrac{x^2}{2} + x\right]_{0}^{3}\\ &= \frac{4}{3} - \left(\frac{2}{3} - \left( \frac{2}{3}(4)^{\frac{3}{2}} - \frac{9}{2} + 3\right)\right)\\ &= 4.5 \text{ square units}. \end{align*} \)

Now let's try using the other formula.

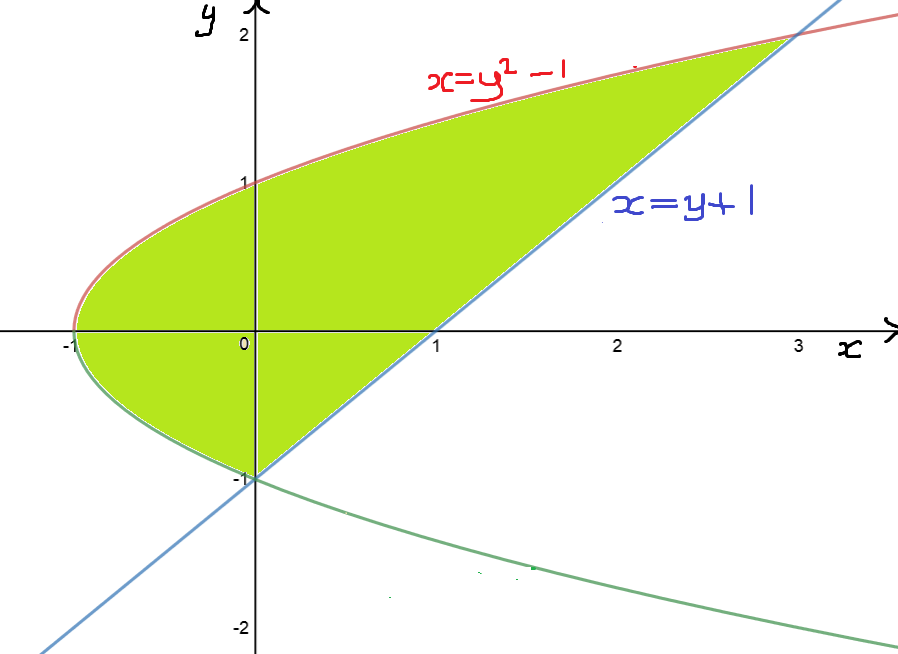
This time, one function \(x = y^2 - 1\) is always on the left, and one function \(x = y + 1\) is always on the right. I'm liking this already! We now need to find the \(y\)-values at the points of intersection so that we can find our limits of integration. But we know what the \(x\)-values are. When \(x = 0\), we can read \(y = -1\) off from the graph. Also, \(x = 3\) must satisfy \(3 = y + 1\), so \(y = 2\). We now have everything we need to calculate the area. Let's go:

\( \begin{align*} A &= \int_{-1}^{2} \text{right} - \text{left}\; dy \\ &= \int_{-1}^{2} y + 1 - (y^2 - 1) \; dy\\ &= \int_{-1}^{2} -y^2 + y + 2\; dy\\ &= \left[-\dfrac{y^3}{3} + \dfrac{y^2}{2} + 2y \right]_{-1}^{2} \\ &= \left(- \dfrac{2^3}{3} + \dfrac{2^2}{2} + 2(2)\right) - \left( - \dfrac{(-1)^3}{3} + \dfrac{(-1)^2}{2} + 2(-1) \right)\\ &= 4.5 \text{ square units}. \end{align*} \)

So we get the same answer. That's a relief! Using the first formula was pretty horrible. There's definitely a case for using the second formula in this question.

Now we have time for one last example. In this example, it's much easier to use the second formula.

Example 6

Find the area of the region bounded by the curves \(x = (y - 1)^2\) and \(x = -y^2 + 5\).

Let's draw the curves so that we can work out which one is to the right, and which is to the left.

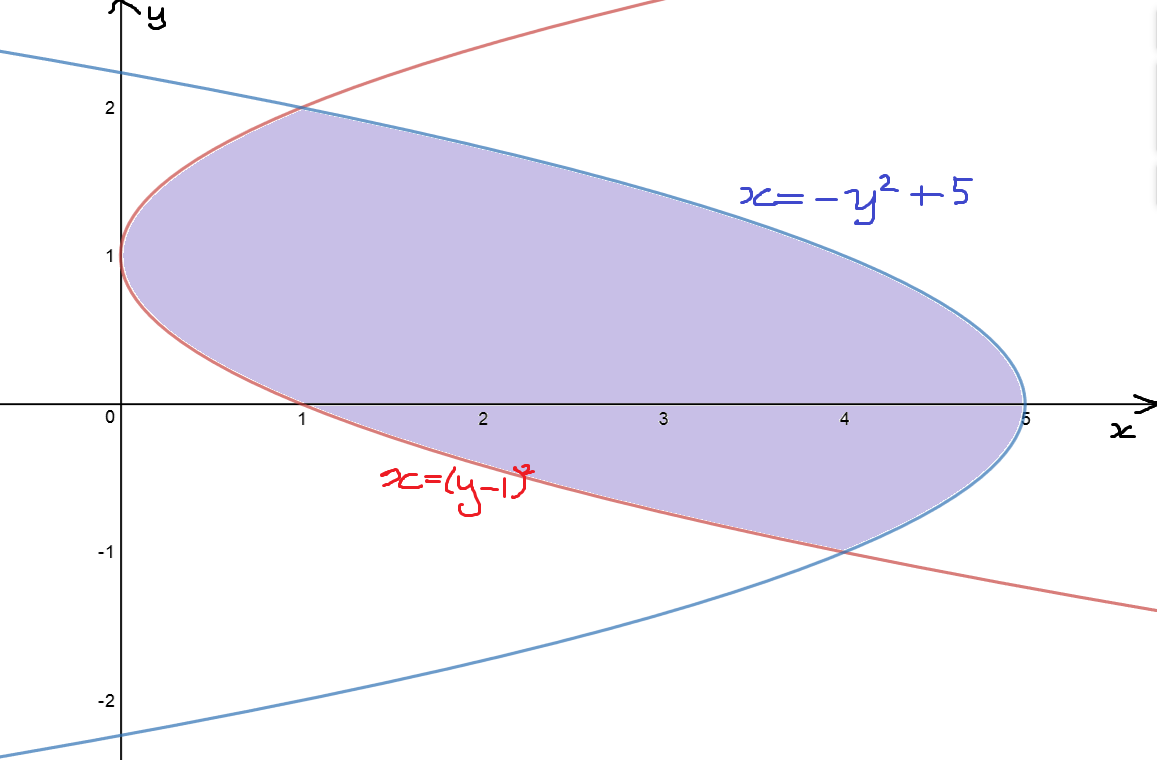
\(x = -y^2 + 5\) is the right-most curve. Now, we need to find the points of intersection. Set the two equations equal, and solve for \(y\):

\( \begin{align*} (y - 1)^2 &= -y^2 + 5\\ y^2 - 2y + 1 &= -y^2 + 5\\ 2y^2 - 2y - 4 &= 0 \\ y^2 - y - 2 &= 0\\ (y - 2)(y + 1) &= 0\\ y &= 2 \text{ and } y = -1 \end{align*} \)

So, our limits of integration will be \(y = -1\) and \(y = 2\). It's time to calculate the area. It will definitely be easier to use the second formula here, and it's all set up nicely for us, anyway. If we tried to use the first formula, we'd have to split the region up into three chunks and calculate three integrals. Off we go:

\( \begin{align*} A &= \int_{-1}^{2} \text{right} - \text{left}\; dy \\ &= \int_{-1}^{2} -y^2 + 5 - (y - 1)^2 \; dy\\ &= \int_{-1}^{2} -2y^2 + 2y + 4 \; dy\\ &= \left[-\dfrac{2y^3}{3} + y^2 + 4y \right]_{-1}^{2} \\ &= \left(- \dfrac{2(2)^3}{3} + 2^2 + 4(2)\right) - \left( - \dfrac{2(-1)^3}{3} + (-1)^2 + 4(-1) \right)\\ &= 9 \text{ square units}. \end{align*} \)

Conclusion

Now it's time for you to get some practise at finding areas between curves. I'd recommend finding some exercises in a book rather than making them up yourself. Don't forget that there are two different formulas that can be used to find the areas between curves:

\( \text{Area Between Curves} = \displaystyle{\int_a^b f(x) - g(x)\; dx} \)

and

\( \text{Area Between Curves} = \displaystyle{\int_c^d f(y) - g(y)\; dy}. \)

Although the first one seems more natural to us, there are times when life is much easier if we apply the second one.

Description

Calculus is the branch of mathematics that deals with the finding and properties of derivatives and integrals of functions, by methods originally based on the summation of infinitesimal differences. The two main types are differential calculus and integral calculus.

Environment

It is considered a good practice to take notes and revise what you learnt and practice it.

Audience

Grade 9+ Students

Learning Objectives

Familiarize yourself with Calculus topics such as Limits, Functions, Differentiability etc

Author: Subject Coach
Added on: 23rd Nov 2017

You must be logged in as Student to ask a Question.

None just yet!

Calculus

Chapters

Finding Areas Between Curves

Finding Areas Between Curves

Finding Areas between Curves

Applying the Area Formulas

Example 1

Steps for finding areas between curves

Example 2

Example 3

Example 4

Example 5

Example 6

Conclusion

Description

Environment

Audience

Learning Objectives

THANK YOU FOR STOPPING BY!