Solids of Revolution

Did you know, if you start out with a function \(y = f(x)\) like the one shown in the graph below ...

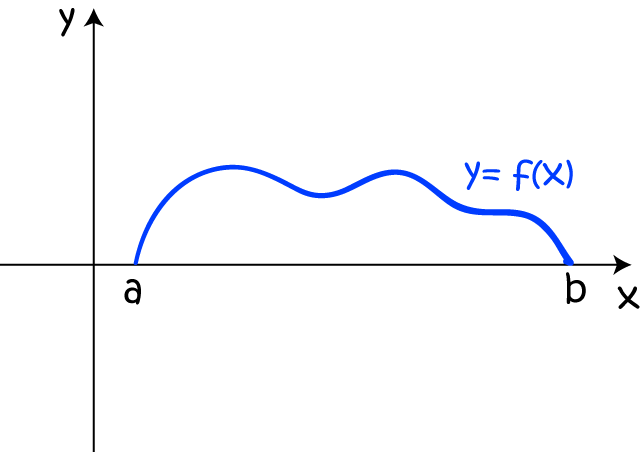
... and rotate it around the \(x\)-axis, you form a solid like this?

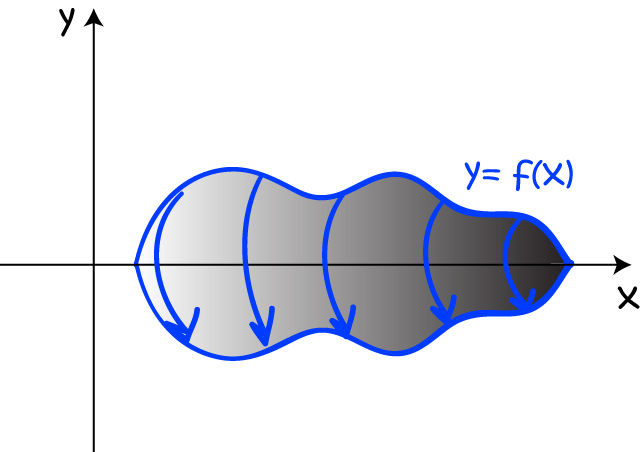
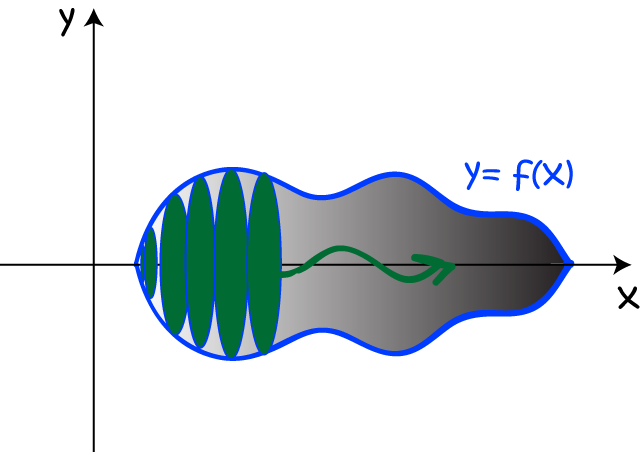
Of course, having done that, mathematicians will want to be able to find the volume of the solid.

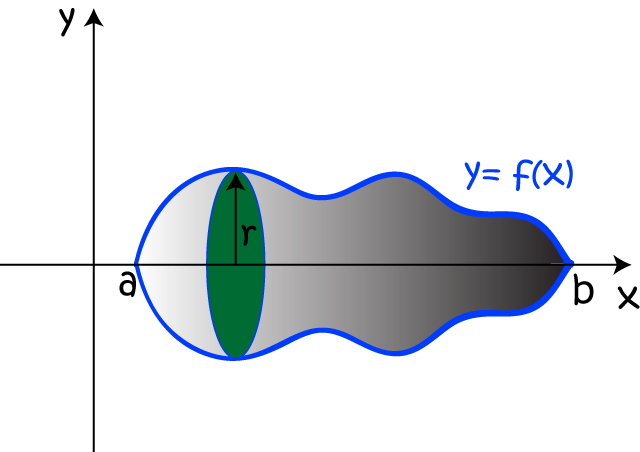
To do that, we stack up a pile of very thin discs, and add their volumes together using integration:

The top of each disc will be a circle whose radius is given by the value of the function \(y= f(x)\) at the point where the disc is stacked:

So, let's calculate that volume! We know that the area of a circle is

and our radius is the value of \(f(x)\) at that point. So, \( A = \pi (f(x))^2. \) Of course, each disc is going to be as thin as possible. As we're adding up the discs in the \(x\)-direction, we'll call this thickness \(dx\). Now we find the volume of the solid by adding up the volumes of all these thin little discs in the \(x\)-direction. In other words, the volume is given by the integral: Remember this formula: it's the formula for the volume of a solid obtained by rotating the graph of the function \(f(x)\) between \(x = a\) and \(x = b\) about the \(x\)-axis. Usually, we pull the \(\pi\) outside like this:

This reminds me of a joke I heard today:

Bad, isn't it? OK, now we've all stopped groaning let's try our new technique out on an example.

Example

What is the volume of the solid obtained by rotating the curve \(y = \dfrac{x}{2}\) between \(x = 0\) and \(x = 2\) about the \(x\)-axis?

We start with the graph of \(y = \dfrac{x}{2} \):

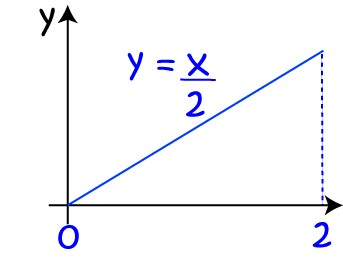
Then we rotate it around the \(x\)-axis to form a cone:

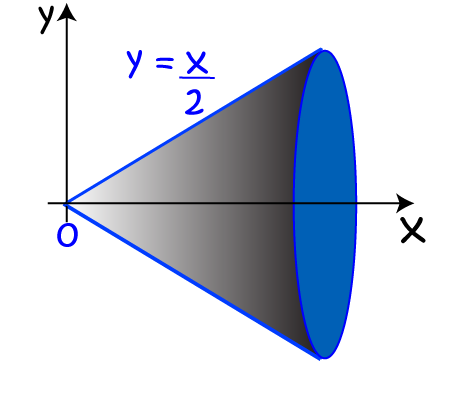
Next, we stack up some discs of thickness \(dx\) to fill in the volume. The radius of each disc will be the function-value \(f(x)\), which is just \(\dfrac{x}{2}\).

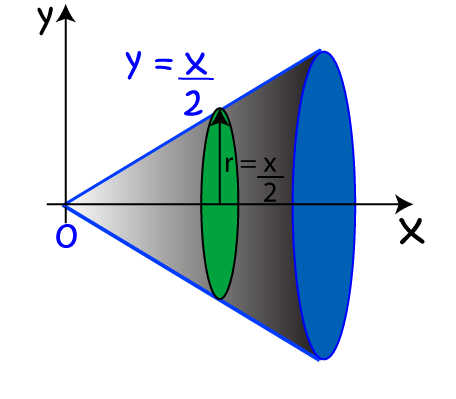
Finally, we sum the volumes of each of these discs together, using an integral, to find the volume of the cone:

Volume of a cone

The general formula for the volume of a cone of base-radius \(r\) and height \(h\) is

The height of our cone was \(2 \text{ units}\), and we calculated its volume as

So, we have \(r^2 h = 2\) and \(h = 2\). Therefore, \(r^2 = 1\), and the base radius of our cone is \(r = 1\). Let's just confirm this base radius using the function definition. The base radius is the value of \(f(2)\), and \(f(2) = \dfrac{2}{2} = 1\), which is what we want. So, the volume we obtained by integration agrees with the general formula for the volume of a cone.

We're not restricted to rotating our graphs about the \(x\)-axis. We can rotate them about any line that is parallel to one of the axes. In the next example, we form a frustum (a sawn-off cone) by rotating a curve about the line \(x = -2\).

Example:

What is the volume of the solid obtained by rotating the curve \(y = \dfrac{x}{2}\) between \(x = 0\) and \(x = b\) about the line \(x = -2\)?

We start with the graph of \(y = \dfrac{x}{2} \):

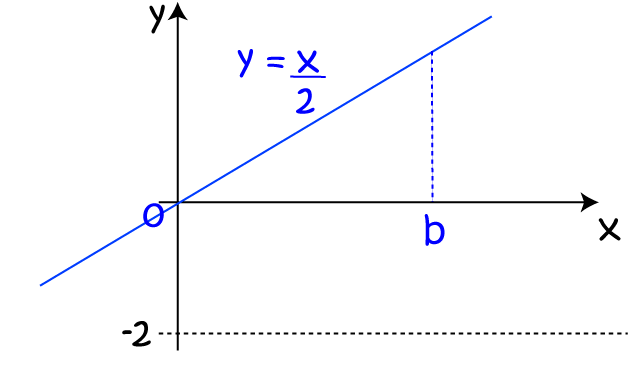
Then we rotate it around the line \(x = -2\) to form a frustum:

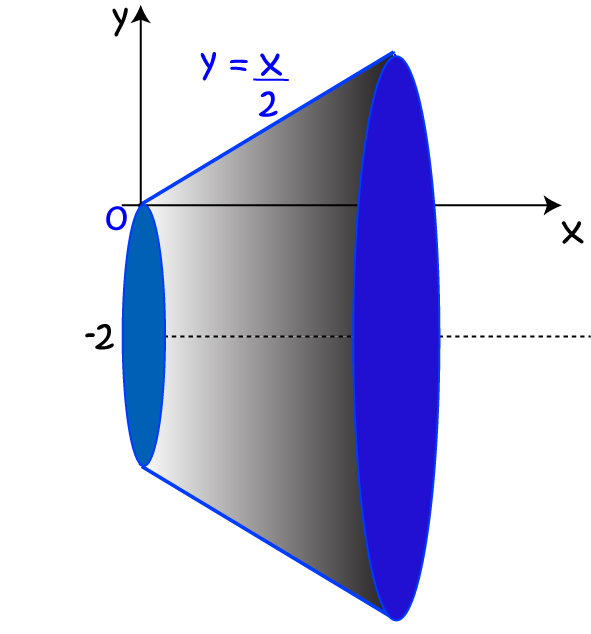
Next, we stack up some discs of thickness \(dx\) to fill in the volume. The radius of each disc will be equal to \(f(x) + 2\), because each point is now 2 units further away from the axis of rotation. So, \(r = \dfrac{x}{2} + 2\).

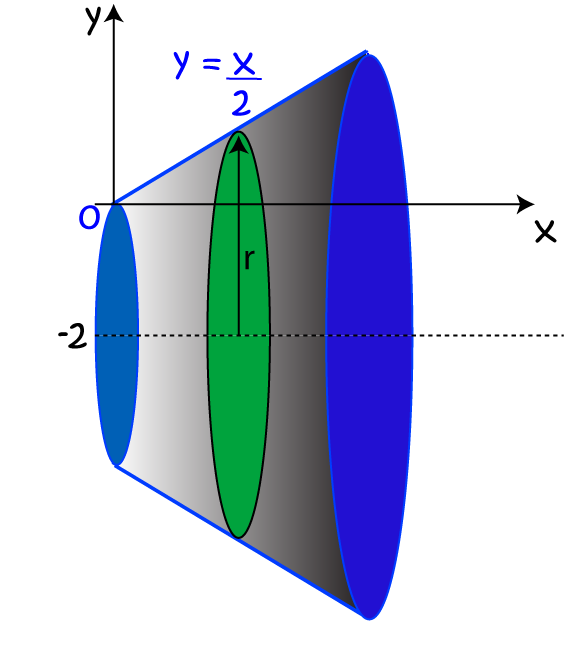
Finally, we sum the volumes of each of these discs together, using an integral, to find the volume of the frustum

Well, rotating all these straight lines is getting a bit boring. Let's try rotating \(y = \sqrt{x}\).

Example

What is the volume of the solid obtained by rotating the curve \(y = \sqrt{x} \) between \(x = 1\) and \(x = 4\) about the \(x\)-axis?

Start by drawing the graph of \(y = \sqrt{x}\):

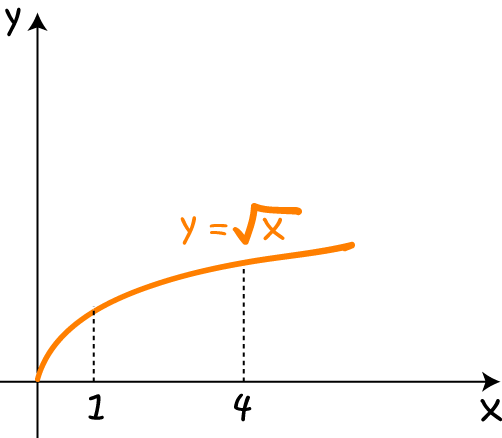
Then rotate the part of the curve between \(x = 1\) and \(x = 4\) around the \(x\)-axis to form the solid below:

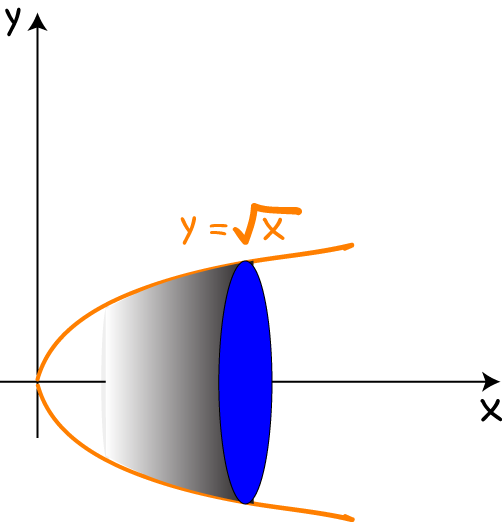
Now, use the formula to find the volume of the solid:

Now, let's try rotating something about the \(y\)-axis.

Example

Find the volume of the solid formed by rotating the curve \(y = x^2\) around the \(y\)-axis between \(y = 1\) and \(y = 4\).

Start by drawing the graph of \(y = x^2\):

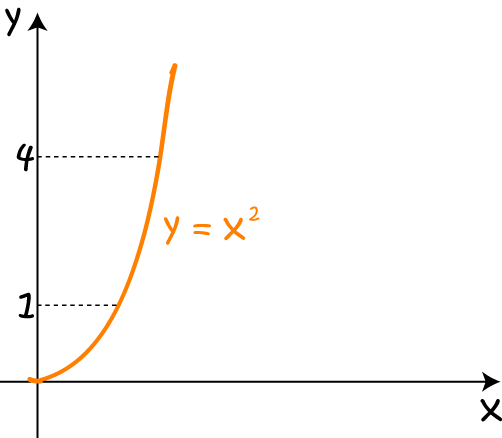
Then rotate it around the \(y\)-axis to form the solid:

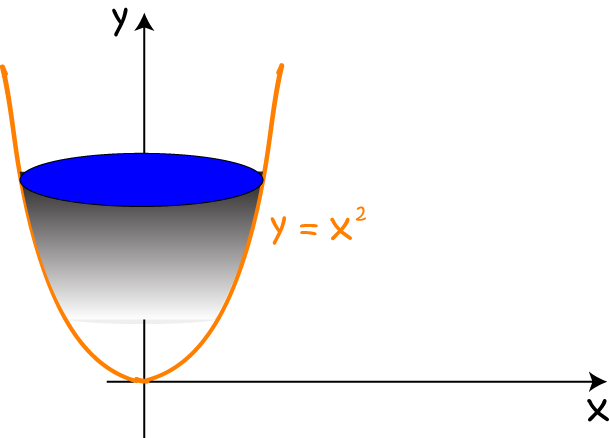
We can come up with a formula for the volume of this solid that is similar to the one for rotating curves around the \(x\)-axis by vertically stacking up discs of thickness \(dy\). We'll then need to express our function in terms of \(y\). Let's call it \(g(y)\). The formula for the volume will be (just changing the \(x\)s to \(y\)s in the formula we found earlier:

To use this formula, we'll need to transform our function into the form \(x = g(y)\):

Now, we're good to go. Let's find our volume:

Rotating the Area Between Two Functions

If we want to form a solid of revolution by rotating the area between two functions about a vertical or horizontal line, and we try to stack up discs, we'll find that any disc we try to draw has a hole in the middle of it. The method used in this case is called the "washer method", precisely because it requires the discs to have those holes in them. It is basically the same as the disc method, except that we need to account for the holes in the middle of our washers. Let's see it in action on an example.

Example:

Find the volume of the solid formed by rotating the region bounded by the graphs of \(y = x^4\) and \(y = x\) about the \(x\)-axis.

We start by drawing the graphs of \(y = x^4\) and \(y = x\) on the same set of axes:

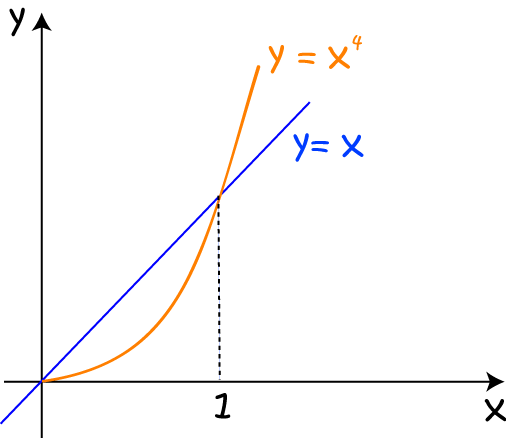
Then we rotate this region around the \(x\)-axis to form our solid:

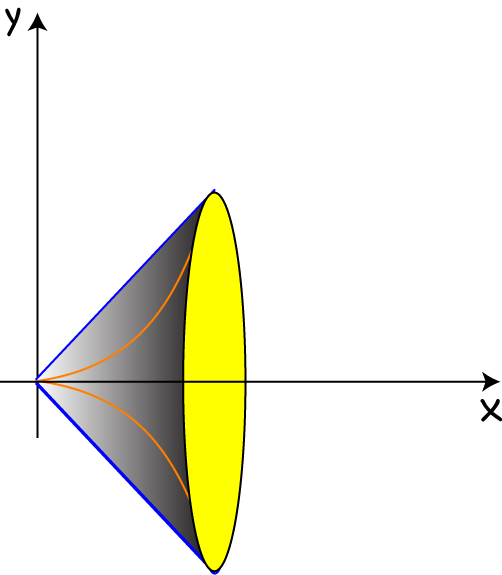
Next, we stack up some washers of thickness \(dx\) to fill in the volume. The outermost radius of each washer will be the function-value of the outermost function, which is \(x\), and the innermost radius of each washer will be the function-value of the innermost function, which is \(x^4\).

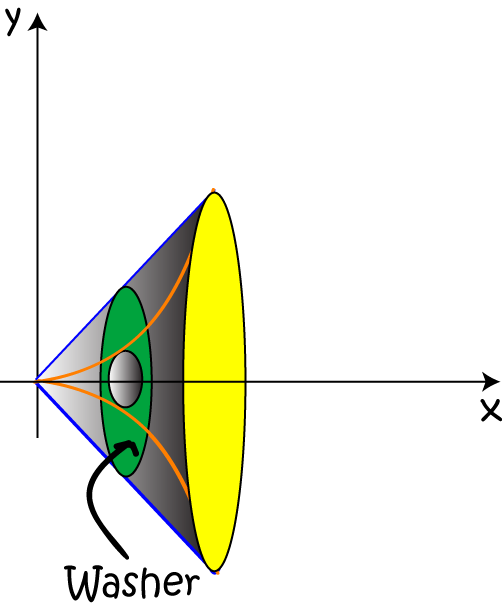
Each washer has the shape of an annulus:

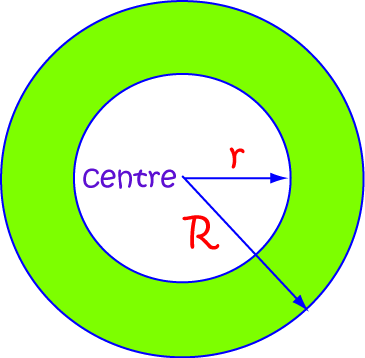
with inner radius \(r = x^4\) and outer radius \(R = x\).

Next, we find where our two curves intersect. We can see from the graph that they intersect at \(x = 1\) and \(x = 0\). These will be our limits of integration. Finally, we sum the volumes of each of these washers together, using an integral, to find the volume of the solid.

Note: Essentially all we've done here is to apply the disc method, with the slight modification that we subtract the inner disc from the outer disc. We're boring a hole formed by rotating \(y = x^4\) around the \(x\)-axis out of the middle of the solid formed by rotating \(y = x\) about the \(x\)-axis.