Calculus
Chapters
Continuous Functions
Continuous Functions
Here's the intuitive idea: a function is continuous if you can draw its graph without lifting your pencil from the paper. In other words, continuous functions are the ones without gaps, jumps or holes. The picture below shows a continuous function:
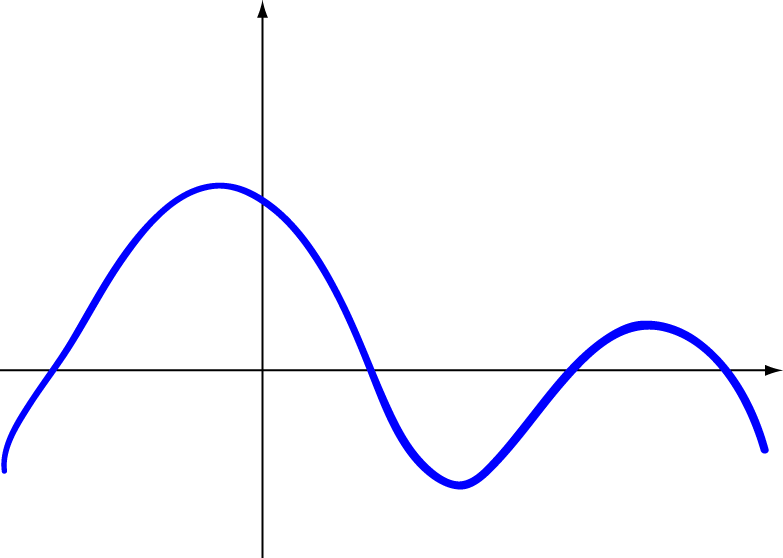
Examples
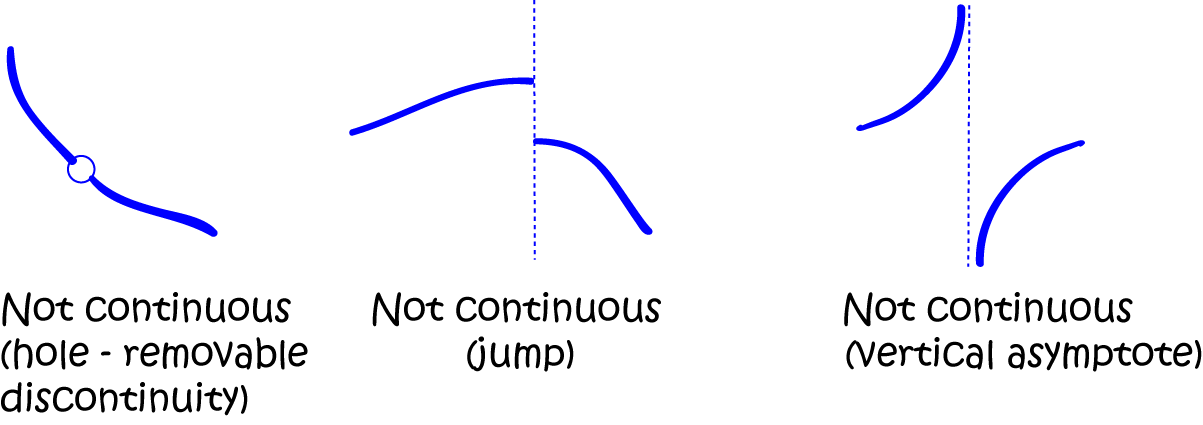
How do we identify functions that aren't continuous (discontinuous)?
The key idea is to look out for holes, jumps or gaps. Holes are called removable discontinuities, jumps are called
jump discontinuities, and gaps are called vertical asymptotes. These three types of problems are shown in the picture
below.
Domains
domain.
The domain of a function is the set of allowable \(x\)-values (or input values)
for the function. Sometimes, the domain of the function is explicitly stated. Other times,
we have to work it out from what the function definition will allow. In these cases, the domain
will be the largest set of \(x\)-values that can be sensibly input into the function definition. For example,
the function \(f(x)= \dfrac{1}{x}\) only makes sense for values of \(x\) that are not equal to zero. Its domain
is the set \(\{x \in \mathbb{R}: x \neq 0\}\). In other words, it's the set of all real numbers that are not equal to zero.
Changing the domain of a function can change whether it's continuous or not.
Example
Is the function \(\dfrac{1}{x + 1}\) continuous?
It's function definition gives us a problem when \(x +1 = 0\), or when \(x = -1\):
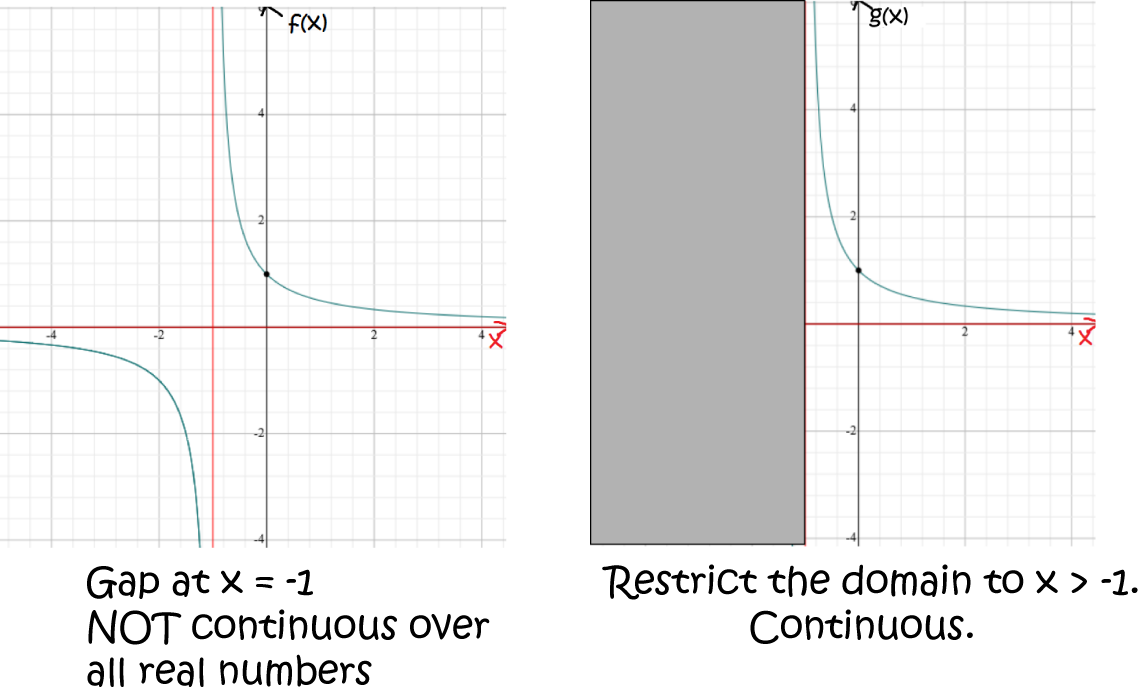
However, if we modify the domain to exclude the gap, we get a continuous function as shown in the picture above.
Let's make those mathematicians happy
So far, we've only talked about the intuitive idea of continuity. It's time to come up with a definition involving symbols and limits that will make these ideas precise. It would be a good idea to read some of the articles on limits (if you haven't done so already) before reading on.
We say that a function \(f\) is continuous if, for every value of \(c\) in its domain,:
- \(f(c)\) is defined, and
- \(\displaystyle{\lim_{x \to c} f(x) = f(c)}\)
This last one's the killer. It's easy to check if \(f(c)\) is defined. For the limit to be defined, the function has to approach the same value as \(x\) approaches \(c\) from all directions. Fortunately, in the real numbers, "in all directions" translates into just two directions: from the left and from the right.
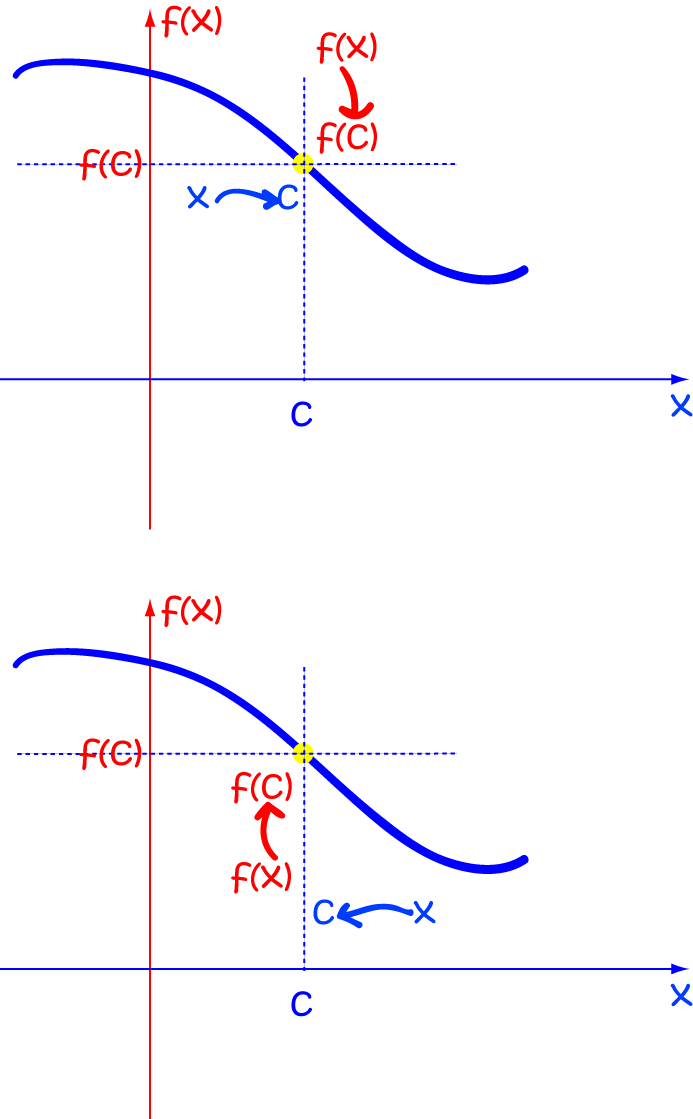
We need to check that as \(x\) approaches \(c\) from the LEFT, \(f(x)\) approaches \(f(c)\), AND
as \(x\) approaches \(c\) from the RIGHT, \(f(x)\) approaches \(f(c)\).
Example
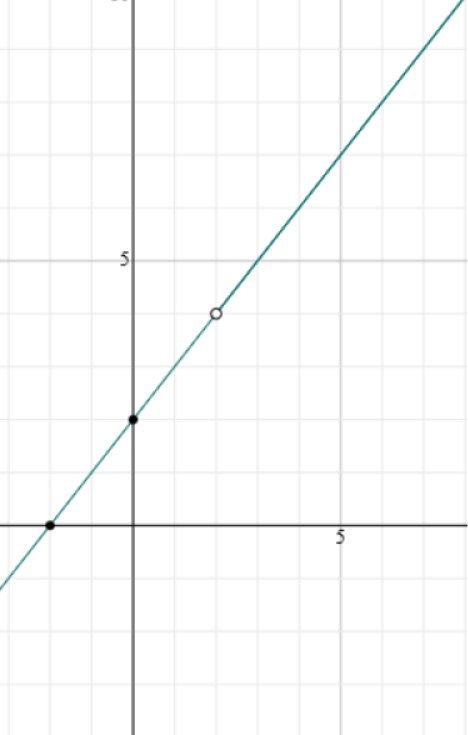
Is the function \(f(x) = \dfrac{x^2 - 4}{x -2}\) continuous over the real numbers?
There is a problem when \(x -2 = 0\), that is, at \(x = 2\). The function is not defined there, so it can't be continuous.
If you check the limits of \(f(x)\) from either side of \(x = 2\) you'll see that they're both equal to \(4\), so
we get a hole in the graph at \(x = 2\). This is called a removable discontinuity.
Note: If we change the domain to be the set of all real numbers \(x\) such that \(x > 2\), then the removable discontinuity is no longer in the domain, and the function is continuous.
Note: Another way to build a continuous function out of \(f(x)\) is to rebuild the function. Here's a new definition of a function that agrees with \(f(x)\) everywhere except at \(x = 2\) and is continuous over the real numbers:
Note: We call removable discontinuities removable because we can "remove" them,
just as we did in the example above, by redefining the function.
Piecewise Functions
You have to take extra care with piecewise functions to make sure their pieces match up at the end-points. The function
To check a piecewise defined function for continuity:
- Check that each branch is continuous.
- Check that the branches match up, so that there are no jumps in the graph.
Let's look at an example:
Example
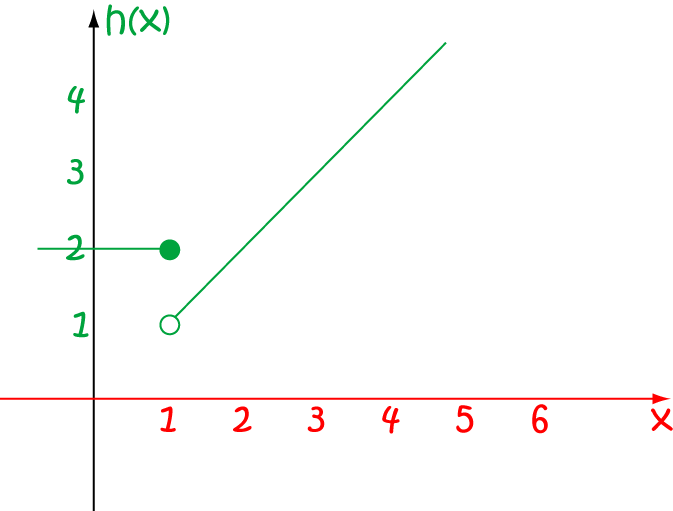
Is the function \(f(x) = \begin{cases} 2 & \text{ if } x \leq 1\\ x &\text{ if } x > 1 \end{cases}\) continuous over the real numbers?
There is no problem for \(x\)-values inside the two branches. The functions \(g(x) = 2\) and \(h(x) = x\) are continuous everywhere.
The function is defined at \(x = 1\): \(f(x) = 2\)
So, the only problem is likely to occur at the end-points of the two branches. Let's see if \(\displaystyle{\lim_{x \to 1} f(x)}\) exists:
- From the left, the function values are all equal to \(2\), so the left-sided limit is 2.
- From the right, the limit is equal to \(\displaystyle{\lim_{x \to 1}x = 1}\).
Since the limits don't match up from the left and right, \(\displaystyle{\lim_{x \to 1} f(x)}\) does not exist, and
the function is discontinuous at \(x = 1\). See the jump in the picture? We call this a jump discontinuity.
Here's an example of a piecewise-defined function that is continuous.
Another example:
This time, we want to look at the absolute value function, \(f(x) = |x|\), which is also piecewise-defined. Just a quick reminder...
Note: Although the absolute value function is continuous at \(x = 0\), it isn't differentiable there. See the article on differentability for further information about differentiability.
Description
Calculus is the branch of mathematics that deals with the finding and properties of derivatives and integrals of functions, by methods originally based on the summation of infinitesimal differences. The two main types are differential calculus and integral calculus.
Environment
It is considered a good practice to take notes and revise what you learnt and practice it.
Audience
Grade 9+ Students
Learning Objectives
Familiarize yourself with Calculus topics such as Limits, Functions, Differentiability etc
Author: Subject Coach
Added on: 23rd Nov 2017
You must be logged in as Student to ask a Question.
None just yet!