Reading:

Calculus

Chapters

Integrals

There are many different uses for integrals. These include finding volumes of solids of revolution, centres of mass, and the distance that Gus the snail has travelled during his attempts on the land-speed record. Definite integrals also have many applications in Physics. One common use of integrals is to find the area under the graph of a function.

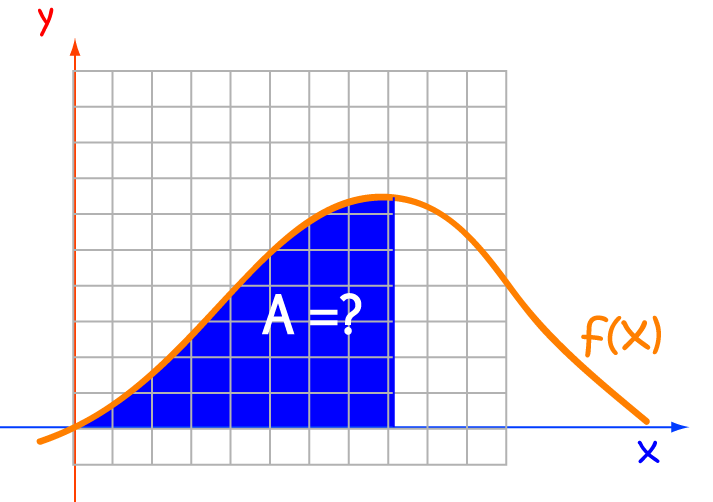
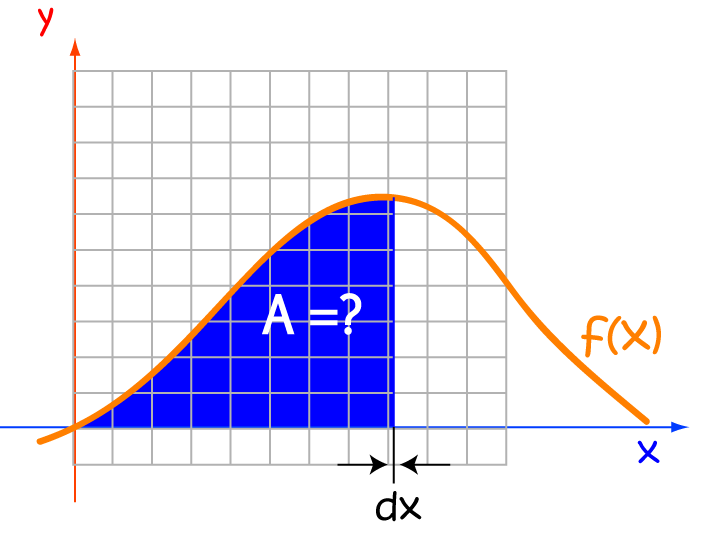
An integral is a giant sum. To find the area under the graph of a function, we add up the areas of little rectangles whose base length approaches zero, as shown in the diagram. Fortunately, we don't often have to calculate these sums. There are rules of integration that can help us out.

Anatomy of an Integral

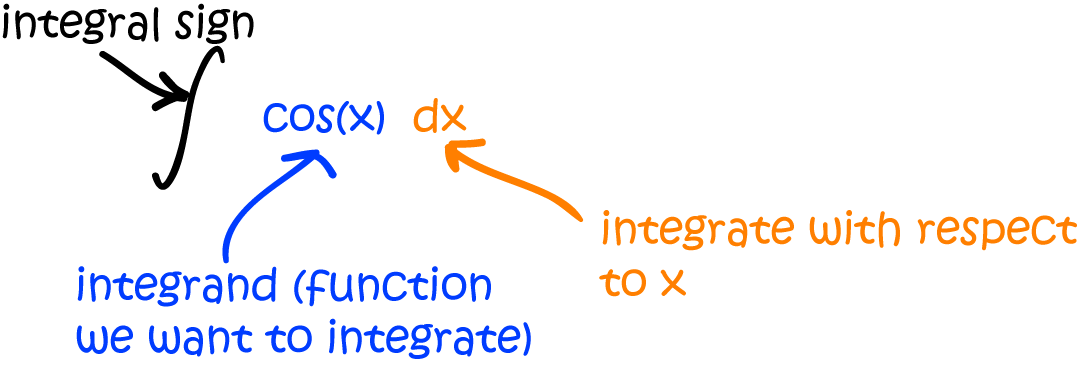
The symbol for an integral looks a bit like an elongated "S". Think of this as "S" for sum. The other parts of the integral are shown in the diagram below: Integrals

Note that the integrand (the function we're integrating) is placed immediately after the integral sign, and the whole thing is finished off with a \(d\text{(variable of integration)}\) to indicate that we're integrating with respect to this variable. Of course, this variable needn't be an \(x\): it could be anything you like. For example, Gus the snail might think of writing:

\( \displaystyle{\int_a^b f(\text{cabbage})\;d\text{cabbage}} \)

to work out the total number of cabbage leaves that were eaten over the period from \(\text{day } a\) to \(\text{day } b\) after his feral caterpillar infestation.

Definite Integrals

As opposed to indefinite integrals, definite integrals have beginning and end values that decorate the integral sign. The bottom value indicates the beginning of the interval, and the value up the top indicates the end value.

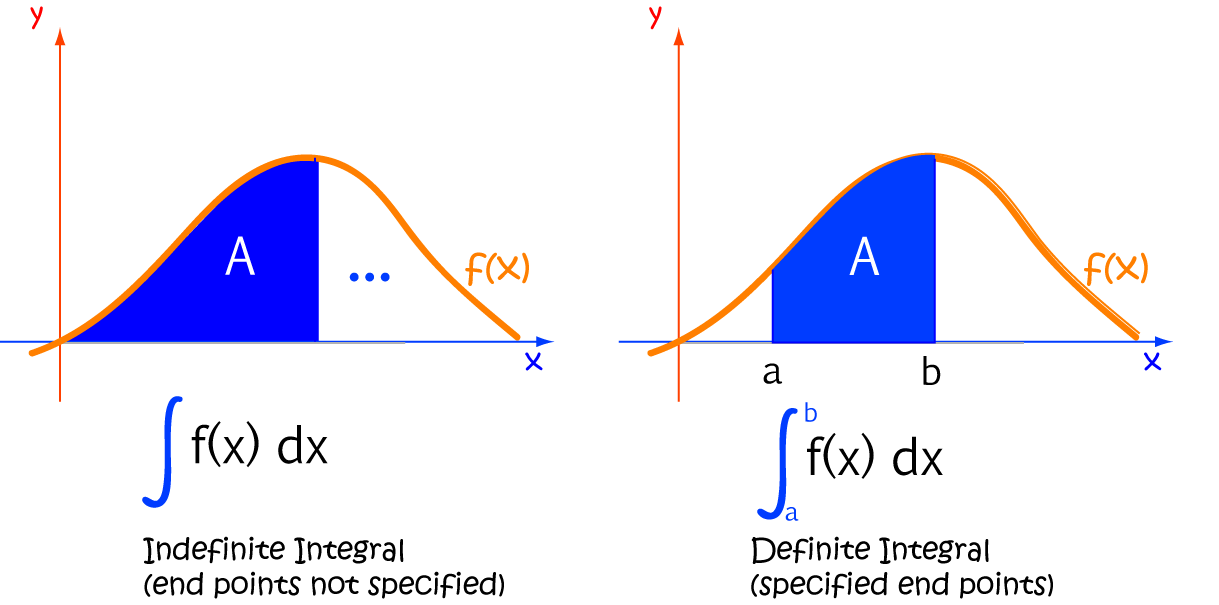
If we can find a function \(F(x)\) (sometimes called a Primitive Function) such that the indefinite integral \(\displaystyle{\int f(x)\;dx = F(x)}\), then the indefinite integral over the interval \((a,b)\) is calculated by evaluating:

\( \displaystyle{ \int_a^b f(x)\; dx = F(b) - F(a)}. \)

We sometimes indicate this using the notation

\( \displaystyle{ \int_a^b f(x)\; dx = [F(x)]_a^b}. \)

Some books might use the notation

\( \displaystyle{ \int_a^b f(x)\; dx = \left. F(x)\right\vert_a^b} \)

to mean the same thing.

Let's see this in action on some examples.

Example

Find the definite integral \(\displaystyle{\int_1^2 (6 - 2x) \; dx}\)

The indefinite integral is given by \(\displaystyle{\int (6 - 2x)\; dx = 6x - x^2 + C}\). Find its values at the end points:

At \(x = 1\): \(\displaystyle{\int (6 - 2x)\; dx = 6(1) - (1)^2 + C = 5 + C}\).
At \(x = 2\): \(\displaystyle{\int (6 - 2x)\; dx = 6(2) - (2)^2 + C = 8 + C}\).

Subtracting these gives the value of the definite integral:

\(\displaystyle{\int_1^2 (6 - 2x)\; dx = (8 + C) - 5 + C = 3 + (C - C) = 3}. \)

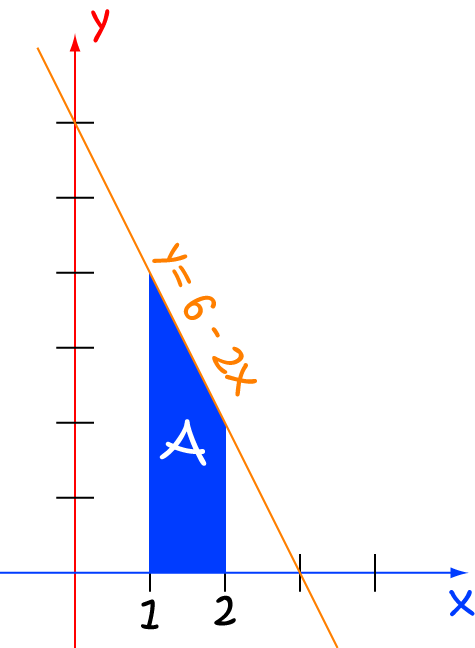
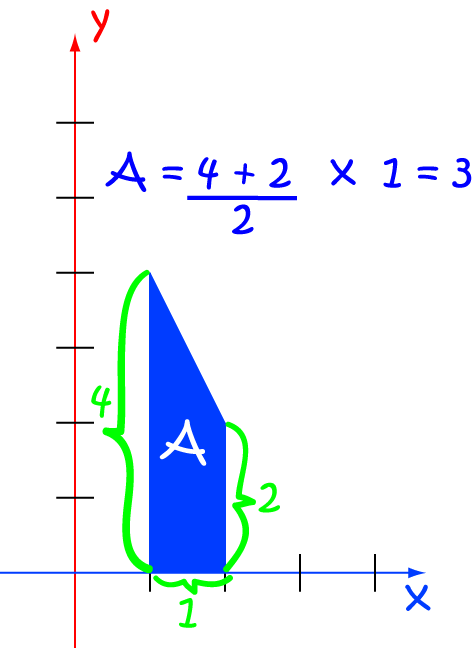
Did you notice how the constants cancelled each other out? This always happens with definite integrals, so you can ignore constants in definite integrals. We can actually write the answer like this:

\(\displaystyle{\int_1^2 (6 - 2x)\; dx = \left[6x - x^2\right]^2_1 = (6(2) - 2^2) - (6(1) - 1^2) = 3}. \)

Remember that the integral should give us the area under the curve? We can use the geometry of this simple example to check that our calculations are correct. The region is a trapezium, so its area is equal to

\( \dfrac{h}{2}(b_1 + b_2), \)

where \(b_1\) and \(b_2\) are the parallel sides of the trapezium. The formula gives us an area of \(3\) for the trapezium, so it looks like we got the integral right!

Time for another example!

Example

Find the definite integral \(\displaystyle{\int_{0.5}^1 \sin (x) \; dx}\)

Don't forget to set your calculator to radians!

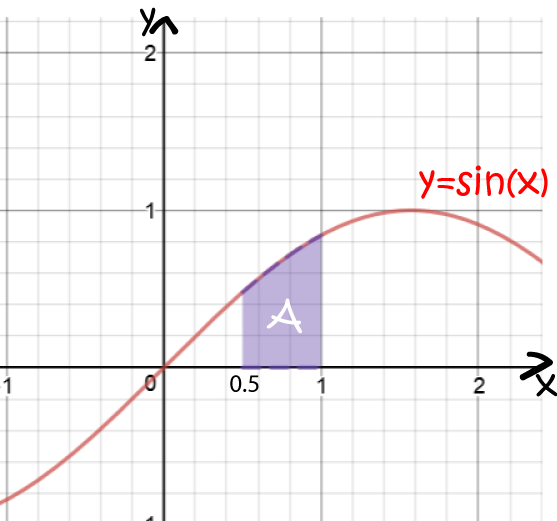
The indefinite integral is given by \(\displaystyle{\int \sin (x) \; dx = - \cos (x) + C}\). As we saw above, we can ignore the \(C\) when we evaluate the definite integral, so:

\(\displaystyle{\int_{0.5}^1 \sin(x)\; dx = [-\cos(x)]^{1}_{0.5} }= ( - \cos (1)) - (- \cos (0.5)) \approx 0.337. \)

The next example shows something to watch out for. Don't assume that the indefinite integral is always zero at \(x = 0\).

Example

Find the definite integral \(\displaystyle{\int_{0}^1 (x^2 + \sin(x)) \; dx}\)

Don't forget to switch your calculator to radians!

The indefinite integral is given by \(\displaystyle{\int (x^2 + \sin(x) )\; dx = \dfrac{x^3}{3} - \cos(x) + C}\). As we saw above, we can ignore the \(C\) when we evaluate the definite integral, so:

\(\displaystyle{\int_{0}^1 (x^2 + \sin(x))\; dx = \left[\dfrac{x^3}{3} - \cos(x) \right]^{1}_{0} = \left( \dfrac{1}{3} - \cos(1)\right) - (-\cos(0)) \approx 0.793.} \)

If we'd assumed that the indefinite integral was zero at \(x = 0\), we would have obtained the incorrect negative answer \(-0.207\).

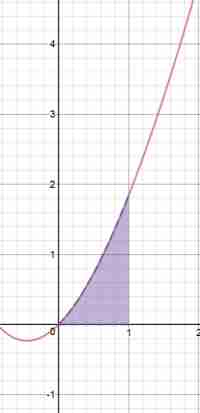
Sometimes we do get negative areas. We need to take care when parts of the curve are below the \(x\)-axis. If you are asked for an integral, just proceed as before. If you are asked for an area, you need to split the integral up and take the absolute values of the integrals of the bits below the \(x\)-axis.

Example

Find the definite integral \(\displaystyle{\int_{0}^2 (x^2 - 2) \; dx}\)

The indefinite integral is given by \(\displaystyle{\int (x^2 -2 )\; dx = \dfrac{x^3}{3} - 2x + C}\). As we saw above, we can ignore the \(C\) when we evaluate the definite integral, so:

\(\displaystyle{\int_{0}^2 (x^2 -2 )\; dx = \left[\dfrac{x^3}{3} - 2x\right]^{2}_{0} = \left( \dfrac{8}{3} - 2(2)\right) - (0) = - \dfrac{4}{3}}. \)

The answer is negative because more of the graph lies below the \(x\)-axis than above it.

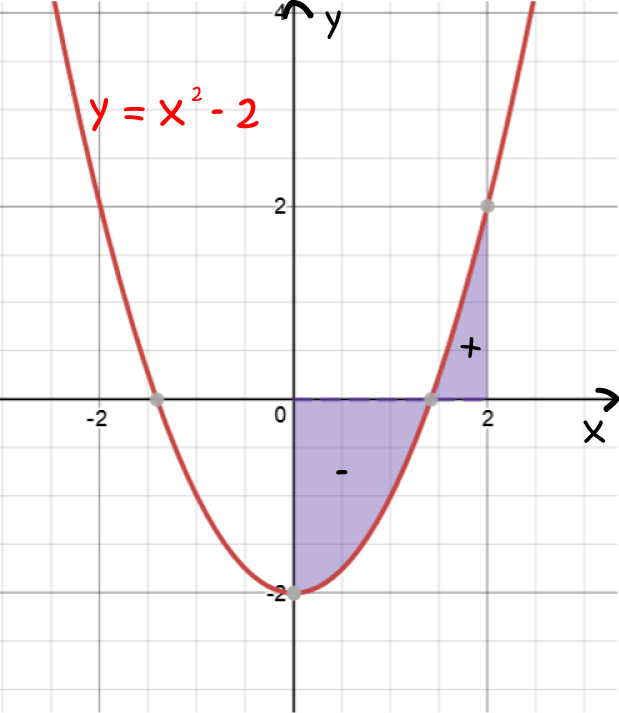
In the next example, we're asked for an area. We need to work out where the graph crosses the \(x\)-axis so that we can split the integral up and take the absolute values of the integrals of the bits below the \(x\)-axis.

Example

Find the area between the graph of \(f(x) = x^2 - 2\) and the \(x\)-axis between \(x = 0\) and \(x = 2\).

This example involves the same function as the preceding one, but this time we're asked for an area, so we need to split the integral up into two sections, and take the absolute value of the integral corresponding to the section under the \(x\)-axis. First, we need to work out where the graph crosses the \(x\)-axis:

\( \begin{align*} x^2 - 2 &= 0\\ x^2 &= 2\\ x&= \pm \sqrt{2}. \end{align*} \)

Only \(\sqrt{2}\) lies between \(x = 0\) and \(x = 2\), so this is where we need to make the split. The section of the graph between \(x = 0\) and \(x = \sqrt{2}\) lies under the \(x\)-axis, so the required area is

\( \text{Area} = \left\vert \displaystyle{\int_0^{\sqrt{2}} (x^2 - 2) \; dx} \right\vert + \displaystyle{\int_{\sqrt{2}}^2 (x^2 - 2)\; dx.} \)

The indefinite integral is given by \(\displaystyle{\int (x^2 -2) \; dx = \dfrac{x^3}{3} - 2x + C}\). As we saw above, we can ignore the \(C\) when we evaluate the definite integrals. Let's evaluate the two parts separately, take the absolute value of the negative one, and then add them together.

From \(x = 0\) to \(x = \sqrt{2}\):

\(\displaystyle{\int_{0}^{\sqrt{2}} (x^2 -2 )\; dx = \left[\dfrac{x^3}{3} - 2x\right]^{\sqrt{2}}_{0} = \left( \dfrac{2\sqrt{2}}{3} - 2\sqrt{2}\right) - (0) = - \dfrac{4\sqrt{2}}{3}}. \)

From \(x = \sqrt{2}\) to \(x = 2\):

\(\displaystyle{\int_{\sqrt{2}}^{2} (x^2 -2 )\; dx = \left[\dfrac{x^3}{3} - 2x\right]^{2}_{\sqrt{2}} = \left( \dfrac{8}{3} - 4\right) - \left(-\dfrac{4\sqrt{2}}{3}\right) = \dfrac{8}{3} - 4 + \dfrac{4\sqrt{2}}{3} = 0.5518 \dots}. \)

So the overall area is

\( \text{Area} = \left\vert -\dfrac{4\sqrt{2}}{3} \right \vert + \dfrac{8}{3} - 4 + \dfrac{4\sqrt{2}}{3} = 2.438 \dots \)

Function Requirements

Continuity

In order to evaluate a definite integral, we need the integrand (the function we are integrating) to be continuous on the interval \((a,b)\). That means it can't contain any jumps, holes or vertical asymptotes. In case you've forgotten, vertical asymptotes occur at \(x\)-values where the function is undefined. As the function approaches these \(x\)-values, the function values approach plus or minus infinity. There are ways around the jumps and holes: we can simply split the function up into parts where it is continuous and add up the definite integrals of the parts. However, vertical asymptotes cause all sorts of problems.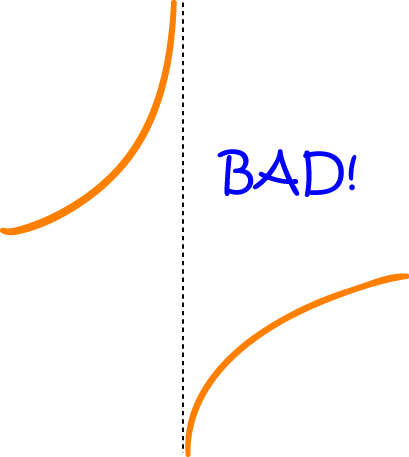

Properties of Definite Integrals

The following properties can help you to split up integrals into chunks that are easy to calculate.

Reversing the Limits

If we reverse the order of the limits, the resulting integral is minus the value of the integral with the limits in the original order: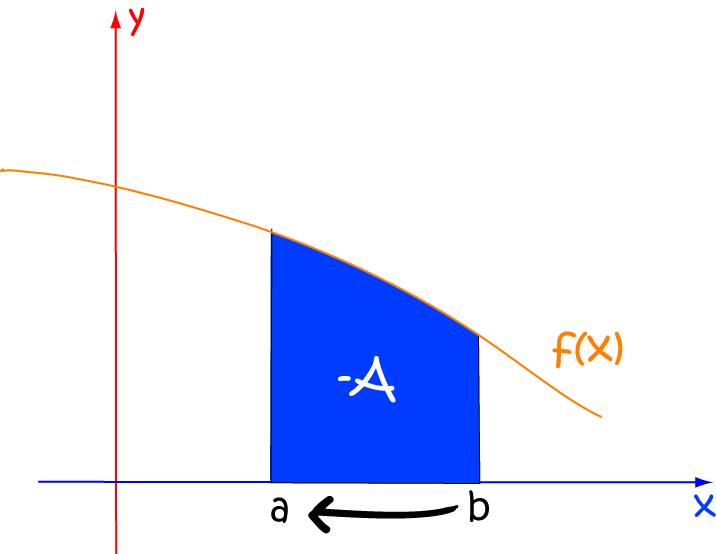

\( \displaystyle{\int^a_b f(x) \; dx = - \int_a^b f(x)\; dx}\)

Both Limits Equal

If both limits are equal, the integral is zero: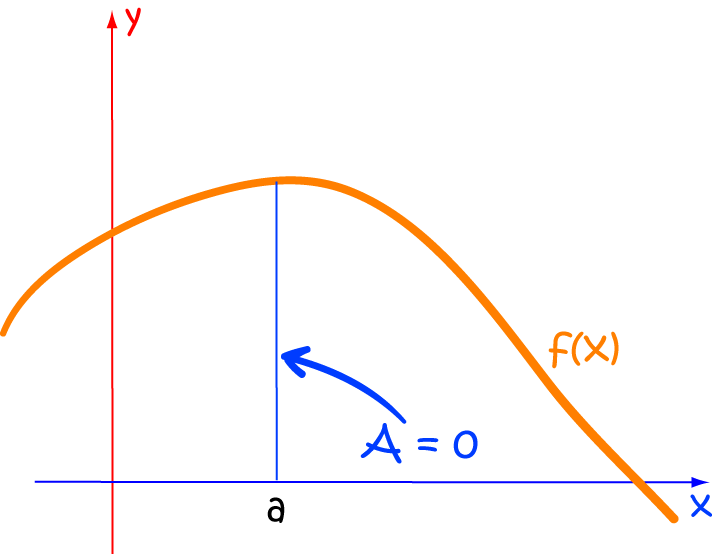

\( \displaystyle{\int^a_a f(x) \; dx = 0}\)

Combining Two Intervals

If two intervals are adjacent, the integral over the combined interval is equal to the sum of the integrals over the two intervals: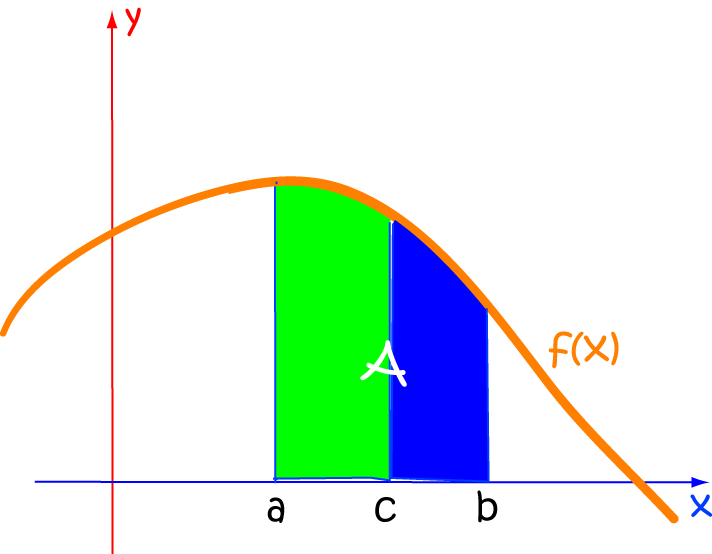

\( \displaystyle{\int_a^c f(x) \; dx + \int^b_c f(x) \; dx = \int_a^b f(x)\; dx}\)

Conclusion

To find a definite integral of \(f(x)\) over the interval \((a,b)\), first find the indefinite integral \(F(x) = \displaystyle{\int f(x)\;dx}\) and evaluate \(F(x)\) at \(a\) and at \(b\). We then have

\( \displaystyle{\int^b_a f(x)\; dx = F(b) - F(a).} \)

This result is called the "Fundamental Theorem of Calculus".

Description

Calculus is the branch of mathematics that deals with the finding and properties of derivatives and integrals of functions, by methods originally based on the summation of infinitesimal differences. The two main types are differential calculus and integral calculus.

Environment

It is considered a good practice to take notes and revise what you learnt and practice it.

Audience

Grade 9+ Students

Learning Objectives

Familiarize yourself with Calculus topics such as Limits, Functions, Differentiability etc

Author: Subject Coach
Added on: 23rd Nov 2017

You must be logged in as Student to ask a Question.

None just yet!

Calculus

Chapters

Integrals

Integrals

Anatomy of an Integral

Definite Integrals

Example

Example

Example

Example

Example

Function Requirements

Continuity

Properties of Definite Integrals

Reversing the Limits

Both Limits Equal

Combining Two Intervals

Conclusion

Description

Environment

Audience

Learning Objectives

THANK YOU FOR STOPPING BY!