Calculus
Chapters
Finding Limits to Infinity
Finding Limits to Infinity
 Sometimes, little kids latch onto the idea of infinity, thinking of it as just a really big number. They talk about 'infinity plus one' and 'infinity infinity',
trying to make even bigger numbers out of infinity.
Sometimes, little kids latch onto the idea of infinity, thinking of it as just a really big number. They talk about 'infinity plus one' and 'infinity infinity',
trying to make even bigger numbers out of infinity.
But we know better! Infinity isn't a number at all. It's the idea we use to describe something that is endless, that 'increases without
bound' like the counting numbers. We can't do arithmetic with infinity in the same way we would add, subtract, multiply or divide normal numbers, but
sometimes we want to know what should happen if we could. In other words, we want to be able to take limits to infinity.
One of the Simplest Limits to Infinity
Perhaps the most common thing we need to do is to work out what the value of \(\dfrac{1}{\infty}\) should be.
We can't just plug
\(\infty\) into \(f(x) = \dfrac{1}{x}\) because we don't know what \(\dfrac{1}{\infty}\) equals - it is undefined. However, we
can look at the value that \(\dfrac{1}{x}\) approaches as \(x\) gets very large and positive.
Let's try finding \(\dfrac{1}{x}\) for some large values of \(x\):
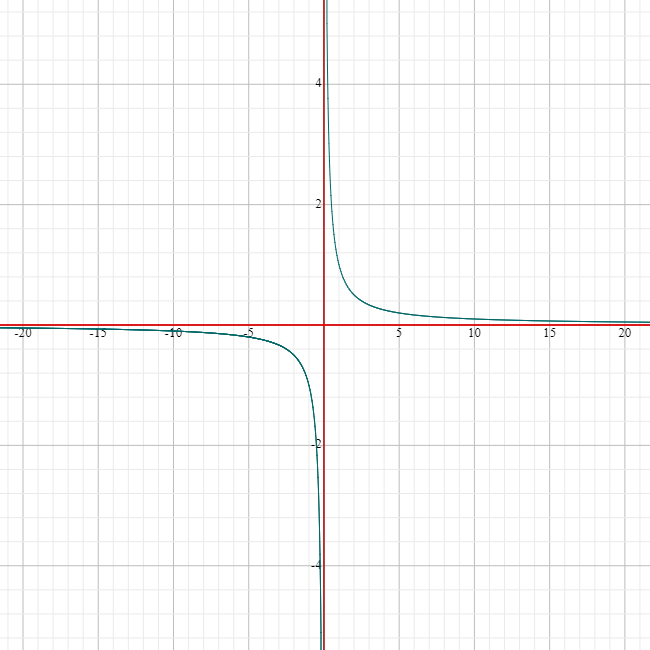
| \(x\) | \(\dfrac{1}{x}\) |
|---|---|
| \(1\) | \(1\) |
| \(2\) | \(0.5\) |
| \(10\) | \(0.1\) |
| \(100\) | \(0.01\) |
| \(1,000\) | \(0.001\) |
| \(10,000\) | \(0.0001\) |
| \(100,000\) | \(0.00001\) |
It looks like the values of \(\dfrac{1}{x}\) are getting closer and closer to \(0\) as the values of \(x\) get larger and larger.
We still don't know what happens when \(x\) reaches infinity, but we do know that \(\dfrac{1}{x}\) is approaching \(0\).
Mathematicians use the idea of a limit to describe this situation where we know what the function-value should
be, but can't actually say what it is, because it is undefined. They say:
The limit of \(\dfrac{1}{x}\) as \(x\) approaches infinity is \(0\)
and write
$$ \lim_{x \to \infty} \left(\frac{1}{x}\right) = 0$$
This is just mathematics-speak for:
As \(x\) approaches infinity, \(\dfrac{1}{x}\) tends to \(0\)
Functions that get bigger and bigger (a.k.a. Limits that Approach Infinity)
Example
What is the limit of the function
Well, as \(x\) gets larger, \(3x\) does too:
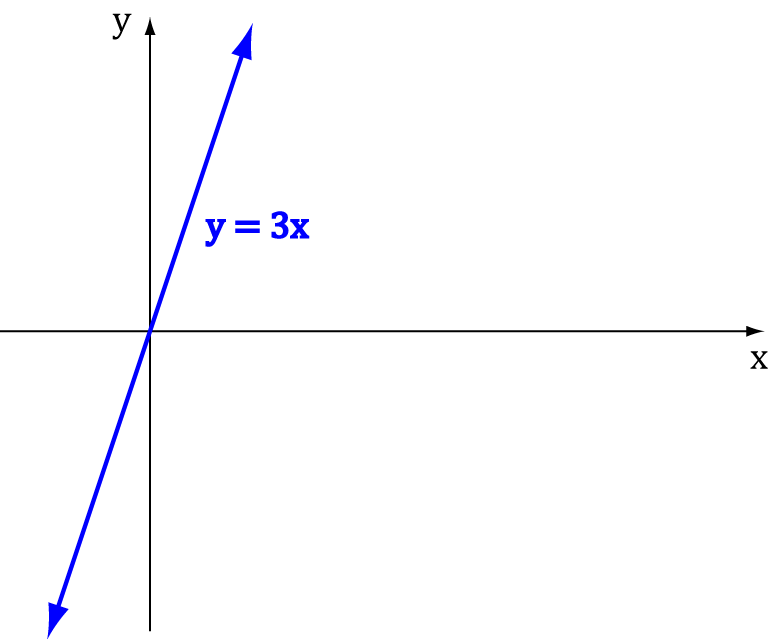
| \(x\) | \(3x\) |
|---|---|
| \(1\) | \(3\) |
| \(2\) | \(6\) |
| \(10\) | \(30\) |
| \(100\) | \(300\) |
| \(1,000\) | \(3,000\) |
| \(10,000\) | \(30,000\) |
| \(100,000\) | \(300,000\) |
| \(\dots\) | \(\dots\) |
So as \(x\) approaches \(\infty\), \(3x\) approaches \(\infty\) too. In symbols, we write:
Remember: \(y = f(x)\) never actually gets to infinity. This just tells us that its values can get as big as you like: \(y\) increases without bound.
How can you tell what a function will do as \(x\) approaches infinity?
When we're dealing with nice friendly functions like polynomials and \(\dfrac{1}{x}\), it's easy! We just have to follow some simple rules:
 |
Functions like \(\dfrac{1}{x}\), \(\dfrac{1}{x^2}\) and \(\dfrac{1}{x^3}\) etc.: These approach \(\mathbf{0}\) as \(x\) approaches \(\infty\) |

|
Functions like \(x\), \(2x\) and \(3x^3\) etc.: These approach \(\infty\) as \(x\) approaches \(\infty\). |
 |
Functions like \(-x\), \(-3x^{17}\) and \(-x^{23}\) etc.: These approach \( - \infty \) as \(x\) approaches \(\infty\). |
What if the functions are more complicated?
Example:
What is the limit as \(x\) approaches \(\infty\) of \(f(x) = 3x^2 - 2x\)?
Let's have a think about this:
- \(3x^2\) goes towards \( + \infty\)
- \(-2x\) goes towards \( - \infty\)
- BUT (major panic) \( \infty + (- \infty)\) is undefined!
Let's calm down and think a bit more: \(3x^2\) heads off to \(\infty\) a lot more quickly than \(- 2x\), so it will dominate the behaviour of the function. In other words, \(f(x)\) will act just like \(3x^2\) as \(x\) heads off towards \(\infty\). So, \(\displaystyle{\lim_{x \to \infty} (3x^2 - 2x) = + \infty}\).
In general, if we look at the highest power of \(x\) in a polynomial function, or a function like \(\dfrac{1}{x^{15}}\), we can figure out what's going on pretty quickly.
When the highest power of \(x\) is:
- Bigger than \(0\), the limit is \( \pm \infty \). The sign depends on the sign of the coefficient of the highest power.
- Smaller than \(0\), i.e. we have \(\dfrac{1}{\text{something}}\), the limit is \(0\).
However, if the highest power of \(x\) is zero, or it's impossible to tell, we have to work harder for the answer.
Rational Functions
Rational Functions are fractions involving polynomials. They look like this: \(f(x) = \dfrac{p(x)}{q(x)}\), where
\(p(x)\) and \(q(x)\) are polynomials.
We can figure out what's going on with the limits of rational functions as \(x\) approaches \(\infty\) by comparing the degrees of \(p(x)\) and \(q(x)\):
The limit of \(\dfrac{p(x)}{q(x)}\) as \(x\) approaches \(\infty\) is:
 |
If the degree of \(p(x)\) is less than the degree of \(q(x)\) |
| A fraction (see below) |
If the degree of \(p(x)\) is equal to the degree of \(q(x)\) |

|
If the degree of \(p(x)\) is greater than the degree of \(q(x)\)
and the sign in front of the term with the largest power of \(x\) is positive: \(\dfrac{p(x)}{q(x)}\) approaches \(\infty\) as \(x\) approaches \(\infty\). |
 |
If the degree of \(p(x)\) is greater than the degree of \(q(x)\)
and the sign in front of the term with the largest power of \(x\) is negative: \(\dfrac{p(x)}{q(x)}\) approaches \(- \infty\) as \(x\) approaches \(\infty\). |
Example
Find \(\displaystyle{\lim_{x \to \infty} \frac{-x^4 - 2x + 2}{3x^3}}\)
Solution:
Because the degree of the top is \(4\) and the degree of the bottom is \(3\), this is going to approach plus or minus infinity.
We need to check the signs of the leading terms of the polynomials before we can decide.
The one on top has a coefficient of \(-1 0\), so it looks like the function values will be negative as \(x\) gets large. Therefore,
So, how do we get those fractions when the degrees of \(p(x)\) and \(q(x)\) are the same? I'm glad you asked. Time for another example!
Example
Find \(\displaystyle{\lim_{x \to \infty} \dfrac{4x^3 + 3}{3x^3 - 7x + 8}.} \)
The degree of \(4x^3 + 3\) is \(3\) as \(x^3\) is the highest power of \(x\), and the degree of \(3x^3 - 7x + 8\) is also \(3\).
Now, the idea is that as \(x\) gets really big, \(4x^3 + 3\) behaves just like \(4x^3\), and \(3x^3 - 7x + 8\) behaves like \(3x^3\).
So
Because we're interested in large values of \(x\), there aren't any pesky zeroes hanging around, so we can cancel out the \(x^3\)s to get
Evaluating Limits
So far, we've been a bit naughty and found the limits by seeing what they 'should' be. There are more formal techniques for finding limits. The article on evaluating limits tells you about some of these.
Description
Calculus is the branch of mathematics that deals with the finding and properties of derivatives and integrals of functions, by methods originally based on the summation of infinitesimal differences. The two main types are differential calculus and integral calculus.
Environment
It is considered a good practice to take notes and revise what you learnt and practice it.
Audience
Grade 9+ Students
Learning Objectives
Familiarize yourself with Calculus topics such as Limits, Functions, Differentiability etc
Author: Subject Coach
Added on: 23rd Nov 2017
You must be logged in as Student to ask a Question.
None just yet!