The Reciprocal Function

The title of this article contains two words that we need to define before we can go any further.

Functions are rules that tell you how to take one object and turn it into another. They take a set of input variables (called the domain) and turn them into a set of output variables (called the range). The input variables are sometimes called arguments of the function. The function has to obey two very important rules:

• It must tell you what to do with every single input variable
• It can only produce one output variable from each input variable

We often call functions names like \(f\) or \(g\), and their input variables names like \(x\) or \(t\). The output variable assigned to the input variable \(x\) by the function \(f\) is called \(f(x)\), which is pronounced "\(f\) of \(x\)".

Although this is the standard notation, there's nothing to stop you calling a function packet and its argument biscuits, so that the output variable is called packet(biscuits), or "packet of biscuits."

Next, we need to define the word reciprocal. To take the reciprocal of something, we simply put 1 over it - like the elephant in this picture. The poor elephant looks like it's getting a bit squashed by that \(1\)! Although there's nothing to stop you calling your input variable "elephant", you might attract a bit of unwanted attention from the animal rights movement.

More commonly, we talk about the reciprocal of a variable like \(x\), and write its reciprocal as \(\dfrac{1}{x}\) or, using index notation, as \(x^{-1}\). Of course, there's one number that you can't take the reciprocal of, and that's \(0\).

The function \(\dfrac{1}{x}\)

The function \(\dfrac{1}{x}\) is often referred to as the reciprocal function. Before we can define a function, we need to specify its domain (or set of input) variables. As we noted above, \(\dfrac{1}{x}\) makes sense for every real number \(x\), except \(0\). So the domain of our reciprocal function will be the set of all real numbers, except for \(0\). We also need to specify the range of our reciprocal function. You can form all real numbers, except for zero, by taking the reciprocal of a real number: if \(x \neq 0\) is a real number, then \(\frac{1}{\left(\frac{1}{x}\right)} = x\). So now we're in business. We can define the reciprocal function
\(f: \mathbb{R}\backslash \{0\} \to \mathbb{R}\backslash \{0\}\) by
\(f(x) = \dfrac{1}{x}\).

Here \(\mathbb{R}\backslash\{0\}\) is just mathematics-speak for the set of all real numbers, except \(0\).

The graph of the reciprocal function looks like this:

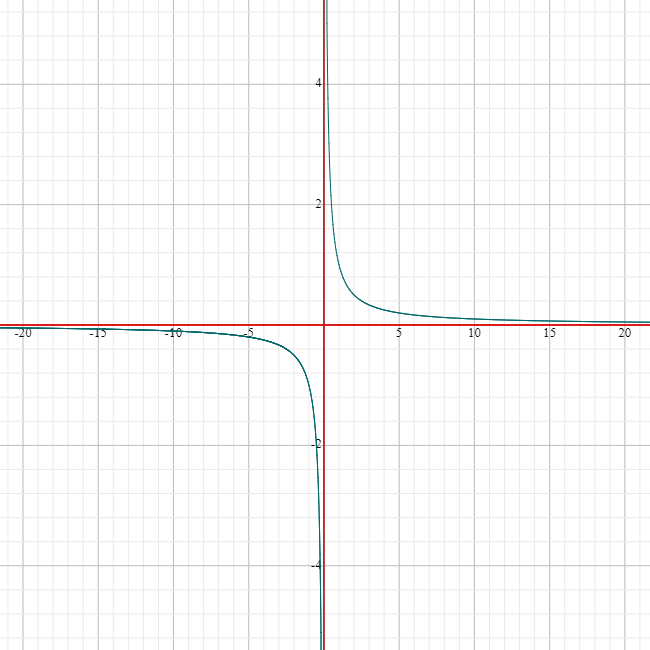
The reciprocal function has some interesting properties:

• The reciprocal of \(1\) is \(1\).
• It is undefined at \(x = 0\): its domain and range are both equal to \(\mathbb{R}\backslash \{0\}\)
• The reciprocals of positive numbers are positive, and the reciprocals of negative numbers are negative
• As \(x\) gets very large and positive, the reciprocal of \(x\) gets very small (close to zero) and positive
• As \(x\) gets very large and negative, the reciprocal of \(x\) gets very small (close to zero) and negative

Asymptotes

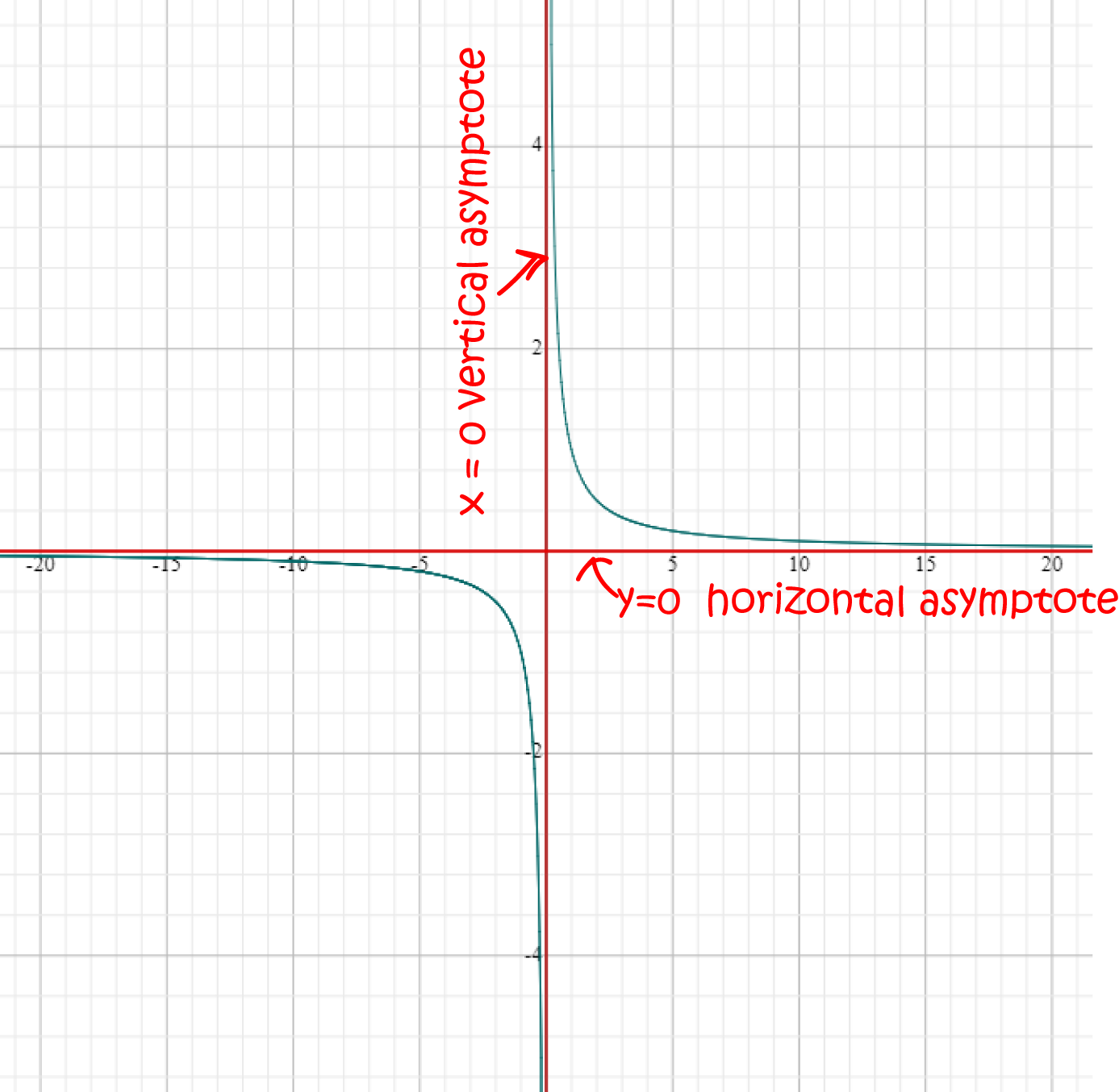
We've just noticed that, as \(x\) gets very large and positive, the values of \(\dfrac{1}{x}\) get very close to zero. However, they never actually reach zero. We call the line \(y = 0\) a vertical asymptote for the graph of \(f(x) = \dfrac{1}{x}\). Asymptotes are straight lines that the graphs of functions get arbitrarily close to as either the input variable \(x\) or the output variable \(y = f(x)\) gets very large. A similar thing happens to the values of the input variable \(x\) as \(y\) gets very large: the graph gets closer and closer to \(y\text{-axis}\) (the line \(x = 0\)), but never actually crosses it. The line \(x = 0\) is a vertical asymptote for the reciprocal function.

Transforming the Reciprocal Graph

Just like any other graph, you can move the graph of the reciprocal function up, down, to the left and to the right. This is accomplished by changing the function definition slightly.

Moving it to the Right

To move the reciprocal graph \(a\) units to the right, subtract \(a\) from \(x\) to give the new function:

\(f(x) = \dfrac{1}{x - a}\),

which is defined everywhere except at \(x = a\).

For example, the graph of the function \(g(x)= \dfrac{1}{x - 3}\) shown below is obtained by moving the graph of \(f(x) = \dfrac{1}{x}\) horizontally, three units to the right.

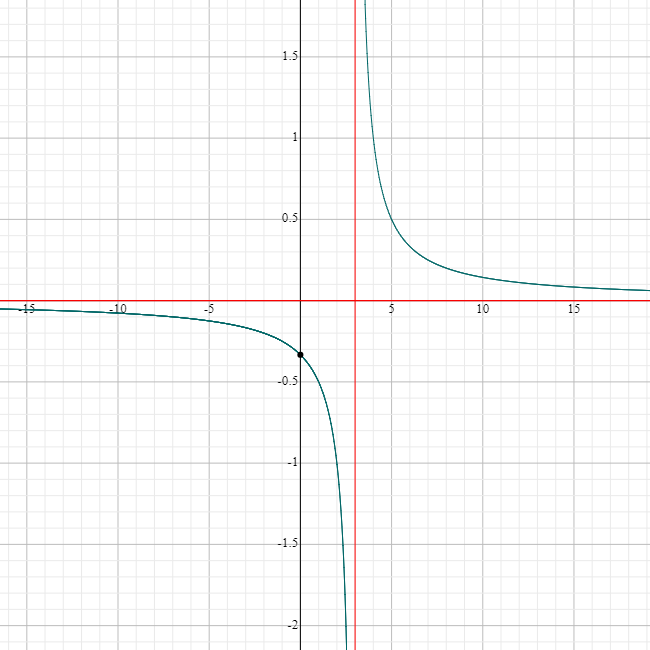
Notice that the vertical asymptote has also shifted \(3\) units to the right, to \(x = 3\), but the horizontal asymptote, \(y = 0\) has stayed in the same place.

Moving it to the left

To move the reciprocal graph \(a\) units to the left, add \(a\) to \(x\) to give the new function:

\(f(x) = \dfrac{1}{x + a}\).

This time, the only problem occurs when \(x = -a\), where we get a vertical asymptote in the graph. There is still no value of \(x\) for which \(f(x) = 0\), and we still have a horizontal asymptote at \(y = 0\).

For example, the graph of the function \(g(x)= \dfrac{1}{x + 3}\) shown below is obtained by moving the graph of \(f(x) = \dfrac{1}{x}\) horizontally, three units to the left.

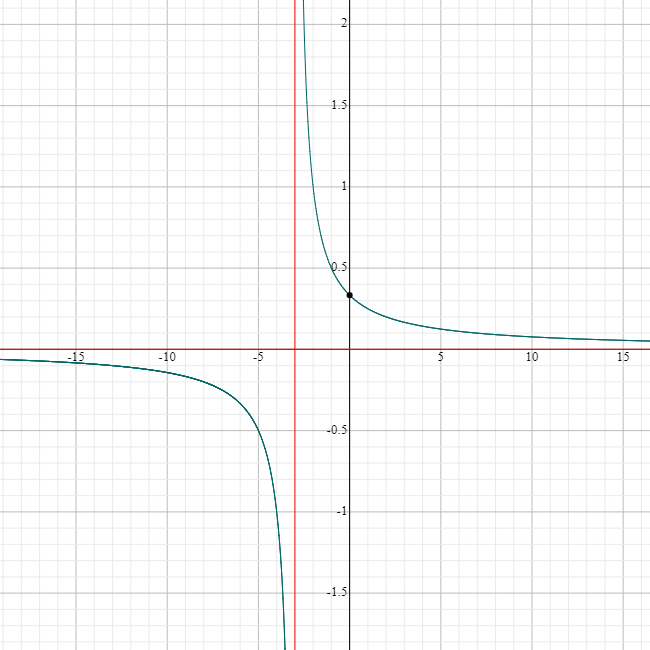
Notice that the vertical asymptote has also shifted \(3\) units to the left, to \(x = -3\), but the horizontal asymptote, \(y = 0\) has stayed in the same place.

Moving it Upwards

To move the reciprocal graph \(a\) units upwards, add \(a\) to \(\dfrac{1}{x}\) to give the new function:

\(f(x) = \dfrac{1}{x} + a\),

which is defined everywhere except at \(x = 0\).

For example, the graph of the function \(g(x)= \dfrac{1}{x} + 2\) shown below is obtained by moving the graph of \(f(x) = \dfrac{1}{x}\) vertically upwards by two units.

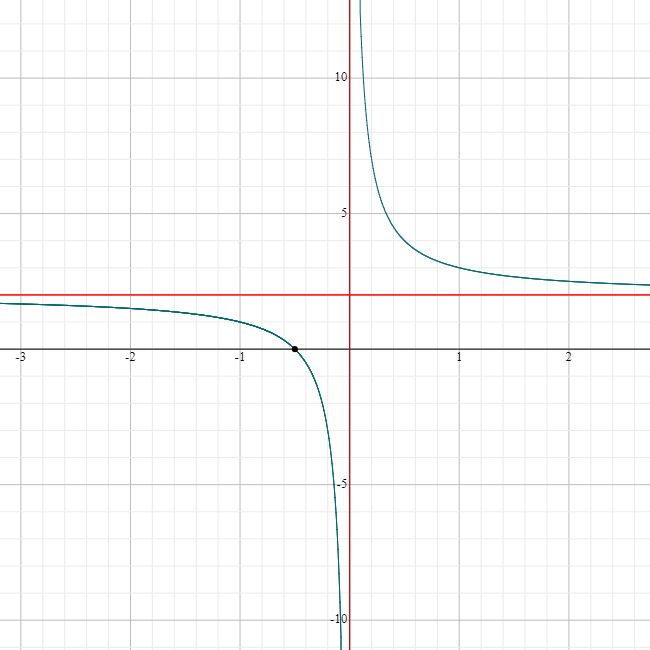
Notice that the horizontal asymptote has also shifted upwards \(2\) units, to \(y = 2\), but the vertical asymptote, \(x = 0\) has stayed in the same place.

Moving it Downwards

To move the reciprocal graph \(a\) units downwards, subtract \(a\) from \(\dfrac{1}{x}\) to give the new function:

\(f(x) = \dfrac{1}{x} - a\),

which is defined everywhere except at \(x = 0\).

For example, the graph of the function \(g(x)= \dfrac{1}{x} - 2\) shown below is obtained by moving the graph of \(f(x) = \dfrac{1}{x}\) vertically downwards by two units.

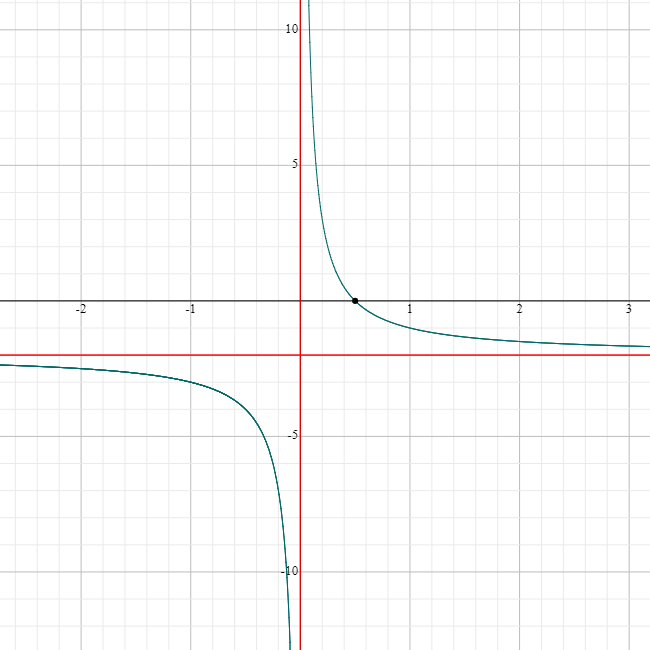
Notice that the horizontal asymptote has also shifted downwards \(2\) units, to \(y = -2\), but the vertical asymptote, \(x = 0\) has stayed in the same place.

Generalising the graphs of reciprocal functions

The graphs of reciprocal functions are examples of hyperbolas. In fact, they are all rectangular hyperbolas, which means that their asymptotes are at right angles to each other. Hyperbolas have many interesting properties that you can read about in the articles on hyperbolas and conic sections.