First Order Differential Equations

Introduction

Differential Equations are equations involving a function and one or more of its derivatives.

For example, the differential equation below involves the function \(y\) and its first derivative \(\dfrac{dy}{dx}\).

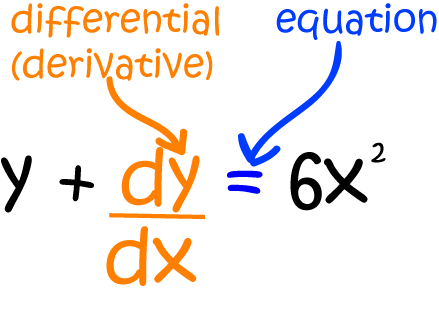
This article will show you how to solve a special type of differential equation called first order linear differential equations. It would be a good idea to review the articles on an introduction to differential equations and solving separable differential equations before you read on.

What are First Order Linear Differential Equations?

First order differential equations are differential equations which only include the derivative \(\dfrac{dy}{dx}\). There are no higher order derivatives such as \(\dfrac{d^2y}{dx^2}\) or \(\dfrac{d^3y}{dx^3}\) in these equations.

Linear differential equations are ones that can be manipulated to look like this:

for some functions \(P(x)\) and \(Q(x)\). The differential equation in the picture above is a first order linear differential equation, with \(P(x) = 1\) and \(Q(x) = 6x^2\).

We'll talk about two methods for solving these beasties. First, the long, tedious cumbersome method, and then a short-cut method using "integrating factors". You want to learn about integrating factors!

Let's start with the long, tedious, cumbersome, (and did I say tedious?) method. Here are the steps you need to follow:

1. Check that the equation is linear.
2. Introduce two new functions, \(u\) and \(v\) of \(x\), and write \(y = uv\).
3. Differentiate \(y\) using the product rule:
   \( \dfrac{dy}{dx} = u \; \dfrac{dv}{dx} + v\;\dfrac{du}{dx} \)
4. Substitute the equations for \(y\) and \(\dfrac{dy}{dx}\) into the differential equation
5. Factorise the parts of the differential equation that have a \(v\) in them.
6. Set the part that you multiply by \(v\) equal to zero.
7. Solve the resulting separable differential equation for \(u\).
8. Substitute \(u\) back into the equation found at step 4.
9. Solve the new equation for \(v\)
10. Now plug \(u\) and \(v\) into \(y = uv\) to yield the solution to the whole equation.

Got that? You'd be forgiven if you hadn't. That's a lot of steps! The best thing to do is to see this in action on an example.

Example

Solve the differential equation \(\dfrac{dy}{dx} - \dfrac{y}{x} = x\)

Step 1: Check the equation is linear:

where \(P(x) = -\dfrac{1}{x}\) and \(Q(x) = x\). So, it is linear.

Let's carry on!
Steps 2,3 and 4: Sub in \(y = uv\) and \(\dfrac{dy}{dx} = u \; \dfrac{dv}{dx} + v\;\dfrac{du}{dx}\):

Step 5: Factorise the bits that involve \(v\):

Step 6: Set the part that you multiply by \(v\) equal to zero:

Step 7: The above equation is a separable differential equation. Solve it using separation of variables:

Step 8: Plug \(u = kx\) back into the equation we found at step 4. Don't forget that the term involving \(v\) is now zero and so it can be ignored:

Step 9: We now have another separable differential equation. Solve it for \(v\):

Step 10: Finally, substitute these expressions for \(u\) and \(v\) into \(y = uv\) to find the solution to the original equation:

That's a lot to remember, isn't it?

Now let's try the sleek, sophisticated, efficient method using integrating factors.

Integrating Factors

Integrating factors let us translate our first order linear differential equation into a differential equation which we can solve simply by integrating, without having to go through all the kerfuffle of solving equations for \(u\) and \(v\), and then stitching them back together to give an equation for \(uv\).

If we have a first order linear differential equation,

then the integrating factor is given by We use the integrating factor to turn the left hand side of the differential equation into an expression that we can easily recognise as the derivative of a product of functions. We can then integrate both sides of our new equation to find the solution of the original differential equation.

Here are the steps we need to follow. There are just a couple less than for the previous method:

• Step 1: Calculate the integrating factor \(I(x) = e^{\int P(x)\;dx}\).
• Step 2: Multiply both sides of the equation by \(I(x)\). The left hand side of the equation will be the derivative of the product \(y\cdot I(x)\).
• Step 3: Integrate both sides of the new equation.
• Step 4: Simplify.

Let's solve our last example using this new method.

Example

Solve the differential equation \(\dfrac{dy}{dx} - \dfrac{y}{x} = x\)

• Step 1: Calculate the integrating factor \(I(x) = e^{\int P(x)\;dx}\):
  \( \begin{align*} I(x) &= e^{\int -\dfrac{1}{x}\; dx}\\ &= e^{-\ln(x)}\\ &= e^{\ln(x^{-1})}\\ &= \dfrac{1}{x}. \end{align*} \)
• Step 2: Multiply both sides of the equation by \(I(x)\). The left hand side of the equation will be the derivative of the product \(y\cdot I(x)\):
  \( \begin{align*} \dfrac{dy}{dx} - \dfrac{y}{x} &= x\\ I(x) \dfrac{dy}{dx} - I(x)\dfrac{y}{x} &= I(x) \cdot x\\ \dfrac{1}{x}\; \dfrac{dy}{dx} - \dfrac{1}{x}\cdot \dfrac{y}{x} &= \dfrac{x}{x}\\ \dfrac{1}{x}\;\dfrac{dy}{dx} - \dfrac{1}{x^2} \cdot y &= 1\\ \dfrac{d}{dx} \left( y \left( \dfrac{1}{x}\right) \right)&= 1 \end{align*} \)
• Step 3: Integrate both sides of the new equation:
  \( \begin{align*} \displaystyle{\int \dfrac{d}{dx} \left( y \left( \dfrac{1}{x}\right)\right)\; dx} &= \displaystyle{\int \; dx}\\ \dfrac{y}{x} &= x + C \end{align*} \)
• Step 4: Simplify.
\( \begin{align*} \dfrac{y}{x} &= x + C\\ y &= x^2 + Cx, \end{align*} \)
which looks very familiar. Wasn't that quicker and easier?

Let's try some more examples.

Example

Solve the differential equation \(\dfrac{dy}{dx} + \dfrac{2y}{x} = \dfrac{e^x}{x^2}\)

• Step 1: Calculate the integrating factor \(I(x) = e^{\int P(x)\;dx}\):
  \( \begin{align*} I(x) &= e^{\int \dfrac{2}{x}\; dx}\\ &= e^{2\ln(x)}\\ &= e^{\ln(x^{2})}\\ &= x^2 \end{align*} \)
• Step 2: Multiply both sides of the equation by \(I(x)\). The left hand side of the equation will be the derivative of the product \(y\cdot I(x)\):
  \( \begin{align*} \dfrac{dy}{dx} - \dfrac{y}{x} &= x\\ I(x) \dfrac{dy}{dx} + I(x)\dfrac{y}{x} &= I(x) \cdot \dfrac{e^x}{x^2}\\ x^2\; \dfrac{dy}{dx} + x^2\cdot \dfrac{2y}{x} &= x^2 \cdot \dfrac{e^x}{x^2}\\ x^2\;\dfrac{dy}{dx} + 2xy &= e^x\\ \dfrac{d}{dx} \left( x^2 y \right)&= e^x \end{align*} \)
• Step 3: Integrate both sides of the new equation:
  \( \begin{align*} \displaystyle{\int \dfrac{d}{dx} \left(x^2 y \right)\; dx} &= \displaystyle{\int e^x \; dx}\\ x^2 y &= e^x + C \end{align*} \)
• Step 4: Simplify.
\( \begin{align*} x^2y &= e^x + C\\ y &= \dfrac{e^x + C}{x^2}. \end{align*} \)
So we have a solution. We get a family of solution curves, one for each different value of \(C\).

Let's try one that's slightly harder.

Example

Solve the differential equation \(\dfrac{dy}{dx} - \dfrac{3y}{x + 1} = (x + 1)^3\)

• Step 1: Calculate the integrating factor \(I(x) = e^{\int P(x)\;dx}\):
  \( \begin{align*} I(x) &= e^{\int -\dfrac{3}{x + 1}\; dx}\\ &= e^{-3\ln(x + 1)}\\ &= e^{\ln((x+1)^{-3})}\\ &= \dfrac{1}{(x + 1)^3} \end{align*} \)
• Step 2: Multiply both sides of the equation by \(I(x)\). The left hand side of the equation will be the derivative of the product \(y\cdot I(x)\):
  \( \begin{align*} \dfrac{1}{(x + 1)^3}\cdot\dfrac{dy}{dx} - \dfrac{1}{(x + 1)^3}\cdot\dfrac{3y}{x + 1} &= \dfrac{1}{(x + 1)^3}\cdot (x + 1)^3\\ \dfrac{1}{(x + 1)^3}\cdot \dfrac{dy}{dx} - \dfrac{3y}{(x + 1)^4} &= 1\\ \dfrac{d}{dx} \left( y \left(\dfrac{1}{(x + 1)^3}\right) \right)&= 1 \end{align*} \)
• Step 3: Integrate both sides of the new equation:
  \( \begin{align*} \displaystyle{\int \dfrac{d}{dx} \left( y \left(\dfrac{1}{(x + 1)^3}\right) \right)\; dx} &= \displaystyle{\int \; dx}\\ \dfrac{y}{(x + 1)^3} &= x + C \end{align*} \)
• Step 4: Simplify.
\( \begin{align*} \dfrac{y}{(x + 1)^3} &= x + C\\ y &= (x + 1)^3(x + C) \end{align*} \)
So, we have a solution. We get a family of solution curves, one for each different value of \(C\).

Let's finish with an example that's harder still.

Example

Solve the differential equation \(\dfrac{dy}{dx} + 4xy = 4x^3\)

• Step 1: Calculate the integrating factor \(I(x) = e^{\int P(x)\;dx}\):
  \( \begin{align*} I(x) &= e^{4x\; dx}\\ &= e^{2x^2} \end{align*} \)
• Step 2: Multiply both sides of the equation by \(I(x)\). The left hand side of the equation will be the derivative of the product \(y\cdot I(x)\):
  \( \begin{align*} e^{2x^2} \cdot \dfrac{dy}{dx} + e^{2x^2}(4xy) &= 4x^3(e^{2x^2})\\ e^{2x^2} \cdot \dfrac{dy}{dx} + (4x e^{2x^2})y &= 4x^3 (e^{2x^2})\\ \dfrac{d}{dx} \left(e^{2x^2}y\right) &= 4x^3 (e^{2x^2}) \end{align*} \)
• Step 3: Integrate both sides of the new equation:
  \( \begin{align*} \displaystyle{\int \dfrac{d}{dx} \left(e^{2x^2}y\right)\; dx} &= \displaystyle{\int 4x^3 (e^{2x^2}) \; dx}\\ e^{2x^2}y &= \text{ a big scary integral.} \end{align*} \)
  To evaluate the integral on the right hand side, we need to use integration by parts. Have a read of the article on integration by parts if you feel you need a refresher. Otherwise, let's go! Try setting \(s = x^2\) and \(dt = 4xe^{2x^2}\). Then \(s' = 2x\) and \(t = e^{2x^2}\), and the integral becomes
  \( \begin{align*} \int 4x^3 e^{2x^2}\; dx &= st - \int t \;ds\\ &= x^2e^{2x^2} - \int 2xe^{2x^2} \; dx\\ &= x^2 e^{2x^2} - \dfrac{1}{2} e^{2x^2} + C \end{align*} \)
• Step 4: Simplify.
\( \begin{align*} e^{2x^2}y &= x^2 e^{2x^2} - \dfrac{1}{2} e^{2x^2} + C\\ y &= x^2 - \dfrac{1}{2} + C e^{-2x^2}. \end{align*} \)
So, we have a solution. Just imagine if we'd tried to do that one using the other technique. It would have taken pages!