Calculus
Chapters
Concavity of Functions
Concavity of Functions
Introduction
Concavity is all about the rate at which the slope of a curve is increasing or decreasing. It has many important
applications in mathematics, not the least of which is to help you decide which part of a hill to cycle up. Unless you are
feeling particularly masochistic, you probably don't want to cycle up parts of a hill where the slope is increasing at an
increasing rate!
There are two types of concavity that are particularly useful in calculus: concave up and concave down.
Let's try and untangle what these terms mean by drawing some pictures.
concave up when
its gradient increases as its values increase. I like to think of a parabola with the ends pointing
upwards
(one that's the 'right way up').
You might have written descriptions of concave up curves in Physics classes. They're the ones that are
'increasing at an
increasing rate' or 'decreasing at a decreasing rate'.
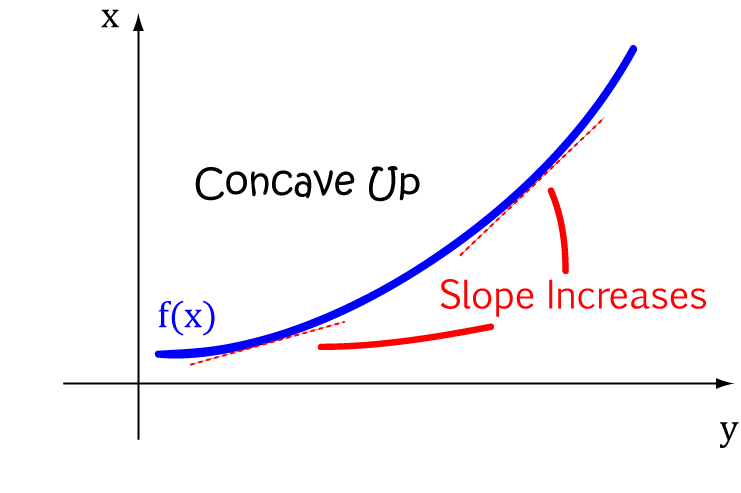 ]
]
concave down when
its gradient decreases as its values increase. I like to think of a parabola with the ends pointing
downwards (one that's 'upside down').
You might have written descriptions of concave down curves in Physics classes. They're the ones that are
'increasing at a
decreasing rate' or 'decreasing at an increasing rate'.
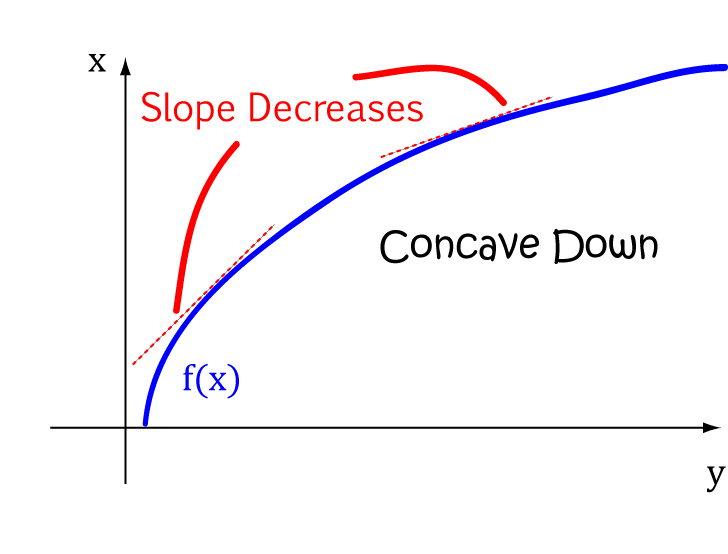
The following pictures show some more curves that would be described as concave up or concave down:
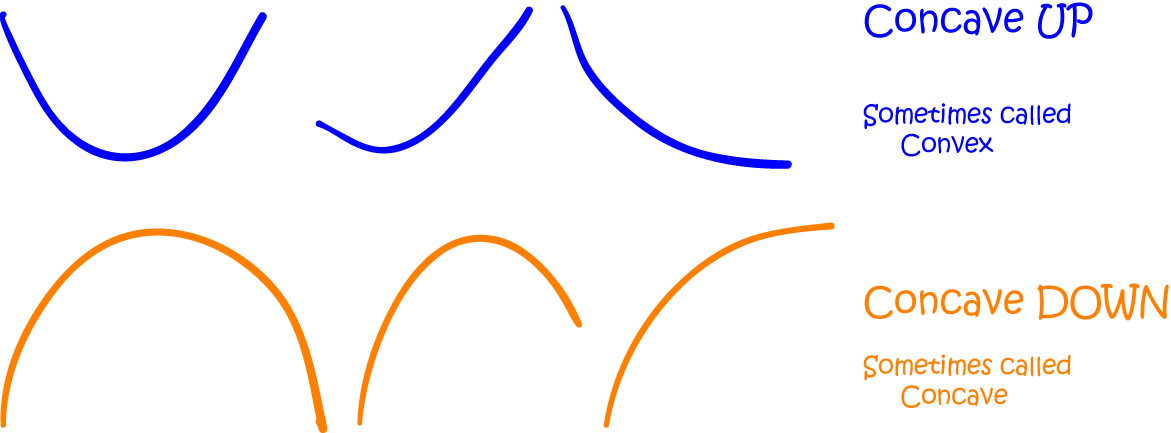
Of course, at this point, someone is going to pipe up and ask what happens when the slope of a curve neither increases nor decreases. In this case, the function is a straight line. As we'll see later, straight lines satisfy the definitions of both concave up and concave down. How's that for muddying the waters? Let's explore more of the gory details about concavity before we get too worried about that.
Finding where a curve is concave up or down
You guessed it, it isn't enough to know what concave up or concave down curves look like! We need to be able to find where curves are concave up or down. A curve can have some parts that are concave up and other parts that are concave down, and it's useful to be able to work out which is which, even before you draw the graph. An understanding of concavity comes in really handy when you need to be able to solve problems like finding the maximum time you can spend playing games on your iPad during a boring class before your teacher finds out... There are also applications in economics and many other fields.
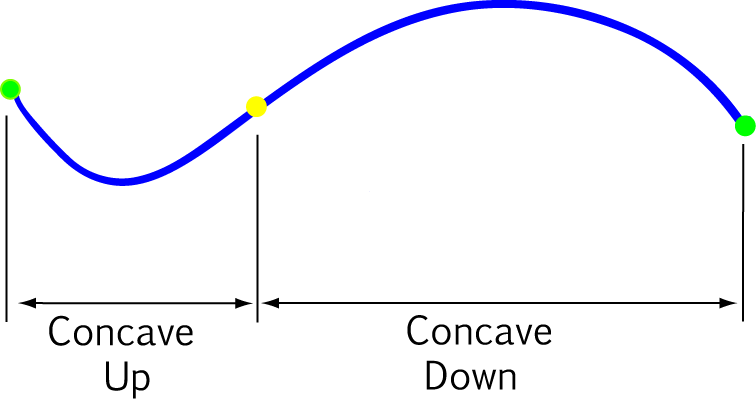
Coming up with a definition (a.k.a. as keeping the mathematicians happy)
The mathematicians aren't satisfied if we say that a curve is concave up if it is increasing at an increasing rate or concave down if it is increasing at a decreasing rate. In fact, you shouldn't be satisfied either: parts of concave up curves can decrease at decreasing rates, and parts of concave down curves can decrease at increasing rates.
So... we first have to ask what's special about curves that are concave up or down. The key idea is that we if we draw a line joining any two points of the curve, it won't cross from one side of the curve to the other. Clear as mud? Hopefully, the pictures below will make this idea a little easier to understand.

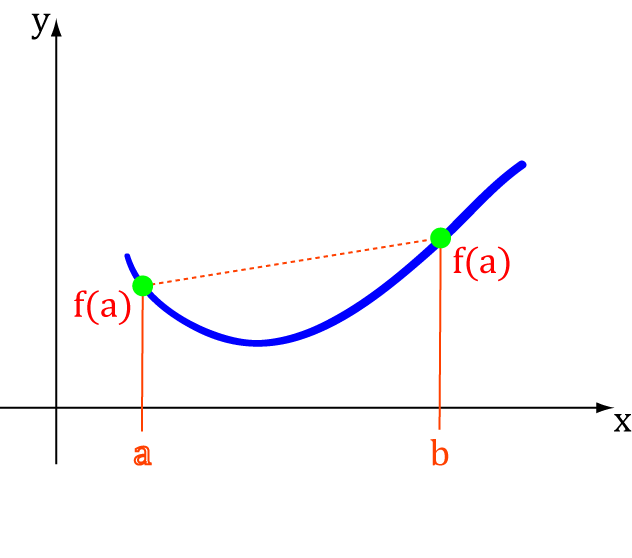
- When \(t = 0\), \(x = 0a + 1b = b\)
- When \(t = 1\), \(x = 1a + 0b = a\)
- When \(t\) moves between \(0\) and \(1\), \(x\) moves between \(a\) and \(b\).
Now, what about the function values corresponding to these \(x\)-values? How do they compare to the points on the line
joining \(f(a)\) to \(f(b)\)?
When \(x = ta + (1-t)b\):
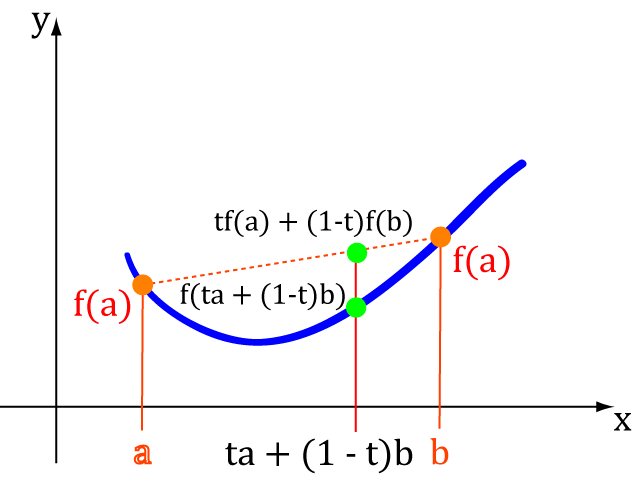
If the function is concave up, then the line needs to stay above or on the curve (and not cross it). So this means:
and if the function is concave down, then the line needs to stay below or on the curve (and not cross it). So we change \(\leq\) to \(\geq\) to give:
These are the definitions that mathematicians actually use to decide whether something is concave up or concave down.
How do I remember which is which?
Some people say that the best way to remember the shape of a concave up curve is using a cup like this:

But I think it's easiest to remember that a function is concave up if its mood is up, so it has a smiley face like this:


Using calculus to help out
Remember, we can use the first derivative to find the slope of a function. However, we want to find out when the slope is increasing or decreasing, so we either need to look at the formula for the slope (the first derivative) and decide, or we need to use the second derivative.
- If a function is concave up, then its second derivative is positive.
- If a function is concave down, then its second derivative is negative.
- To find out what happens when the second derivative is zero, read the article on points of inflection.
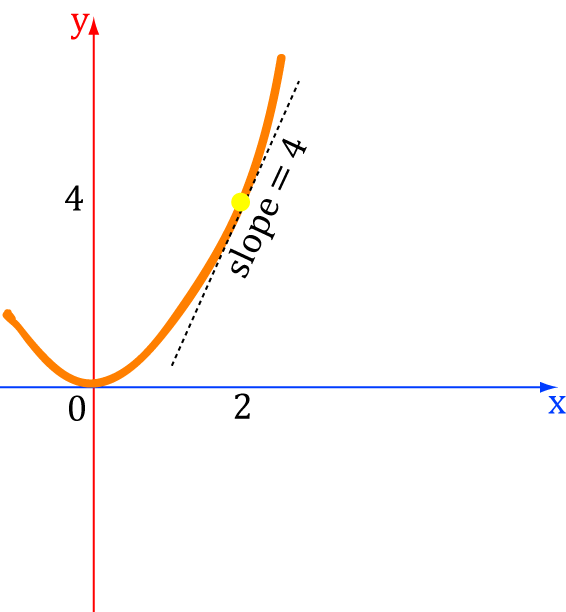
Example:
Let's see if we can use the derivatives to tell us that it is concave up:
The first derivative is \(2x\), which is always increasing. So the first derivative tells us the graph is concave up.
The second derivative is \(2\), which is positive! So the second derivative test tells us that the graph is concave up.
Both tests give us the correct answer! This function is definitely concave up!
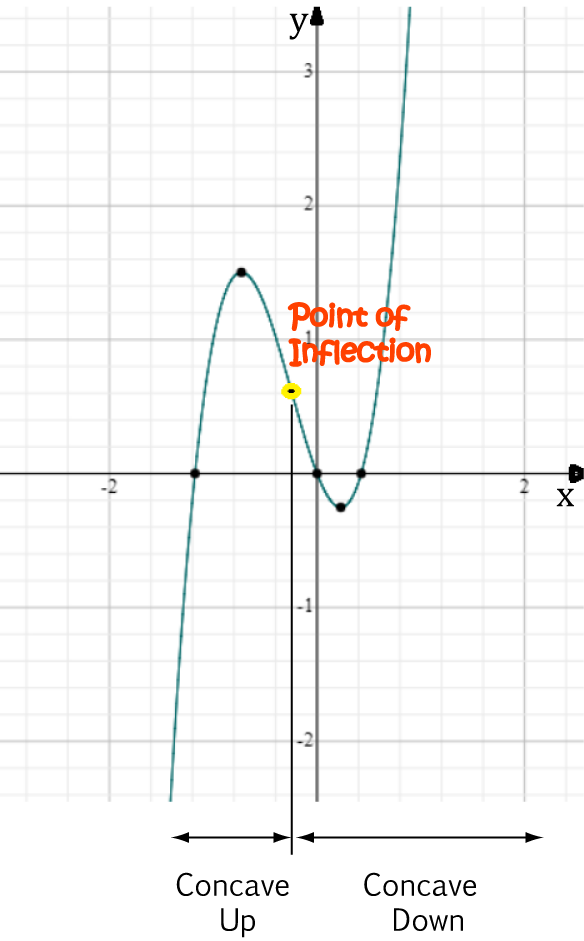
Example
Start by finding the second derivative:
- \(y' = 12x^2 + 6x - 2\)
- \(y'' = 24x + 6\)
Let's look at the sign of the second derivative to work out where the function is concave up and concave down:
- For \(x
- For \(x > -\dfrac{1}{4}\), \(24x + 6 > 0\), so the function is concave up.
Note: The point where the concavity of the function changes is called a point of inflection. This happens at \(x = - \frac{1}{4}\).
Finally, what about straight lines?
Earlier we mentioned that the slope of straight lines neither increases nor decreases: it always stays the same.
This means that you can choose to say that a straight line is concave up or concave down. A straight line \(f(x) = mx + b\) satisfies the definitions of both concave up and concave because we always have
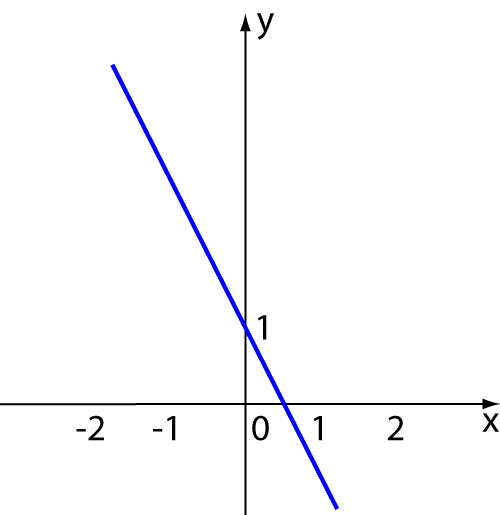
Example:
\(y = -2x + 1\) is a straight line.
It is both concave up and concave down.
The second derivative is always zero:
- \(y' = - 2\)
- \(y'' = 0\)
Description
Calculus is the branch of mathematics that deals with the finding and properties of derivatives and integrals of functions, by methods originally based on the summation of infinitesimal differences. The two main types are differential calculus and integral calculus.
Environment
It is considered a good practice to take notes and revise what you learnt and practice it.
Audience
Grade 9+ Students
Learning Objectives
Familiarize yourself with Calculus topics such as Limits, Functions, Differentiability etc
Author: Subject Coach
Added on: 23rd Nov 2017
You must be logged in as Student to ask a Question.
None just yet!