Calculus
Chapters
Partial Derivatives
Partial Derivatives
Introduction
Warning: Partially pretend this article doesn't exist until you've read the articles on rules of differentiation, the chain rule, the product rule, the power rule, the sum and difference rules and notation for derivatives.
Calculus is all about rates of change. Sometimes functions depend on more than one variable. To find their rates of change, we need to look at the partial derivatives of the function with respect to the different variables. This isn't as difficult as it sounds: we simply pretend the other variables are constants, and differentiate with respect to the one variable we're interested in. We'll need to learn some new notation, but we'll talk more about that later.
Let's start by thinking about a useful real world problem that you probably won't find in your maths textbook.
 For the last few weeks, Sid the sloth has been climbing a vine-covered wall.
The number of leaves that he can eat at position \((x,y)\) on the wall is given by the function:
For the last few weeks, Sid the sloth has been climbing a vine-covered wall.
The number of leaves that he can eat at position \((x,y)\) on the wall is given by the function:
\(\text{leaves}(x,y) = 3x^2 + 2xy\).
Sid wants to know whether his rate of consumption of leaves in the \(x\)-direction exceeds his rate of consumption of leaves in the \(y\)-direction at position \((2,3)\) on the wall.This problem involves the rates of change of the two-variable \(\text{leaves}\) function in the \(x\) and \(y\) directions. To work these out, we need to hold \(y\) constant and differentiate with respect to \(x\), and then hold \(x\) constant and differentiate with respect to \(y\). To do this, we need to learn about
partial derivatives.
Partial Derivatives
If we want to differentiate a function of one variable, such as
\(f(x) = x^3\),
we use the power rule to obtain:
\(f(x) = 3x^2\)
But, what about functions of two or more variables like Sid's leaves function? How do we go about differentiating them?
The answer is that we need to use partial derivatives. We can find partial derivatives with respect to each of the variables of
the function. To find the partial derivative with respect to \(x\), we pretend that \(y\) is a constant, and then differentiate the function with
respect to \(x\) as usual. To find the partial derivative with respect to \(y\), we pretend that \(x\) is a constant, and then differentiate the function as usual,
with
respect to \(y\). Let's have a look at an example so that we can make sense of this.
Consider the function \(f(x,y)\) of the two variables \(x\) and \(y\) that is defined below:
Hold the bus! What did we just do?
- First, we differentiated \(x^3\) with respect to \(x\) using the power rule. The derivative is \(3x^2\).
- Next, we pretended that \(y\) was a constant. It could be \(17\) or whatever you like. Now, if \(y\) is a constant, then so is \(y^2 = (17)^2 = 289\). So, its derivative with respect to \(x\) is zero.
- Finally, we added the derivatives together to get \(f_x(x,y) = 3x^2 + 0 = 3x^2\).
What if we want to differentiate it with respect to \(y\) now? Well, we do the same thing, except that this time, we pretend that \(x\) is the constant. Let's have a go:
So, what did we do this time?
- First, we pretended that \(x\) was a constant. It could be \(6\) or whatever you like. Now, if \(x\) is a constant, then so is \(x^3 = (6)^3 = 216\). So, its derivative with respect to \(y\) is zero.
- Next, we differentiated \(y^2\) with respect to \(y\) using the power rule. The derivative is \(2y\).
- Finally, we added the derivatives together to get \(f_x(x,y) = 0 + 2y = 2y\).
So it really isn't as tricky as it looks, is it? We just have to remember to pretend that all the variables, except the one we're differentiating with respect to, are constants. Let's see this in action on a few examples.
Example:
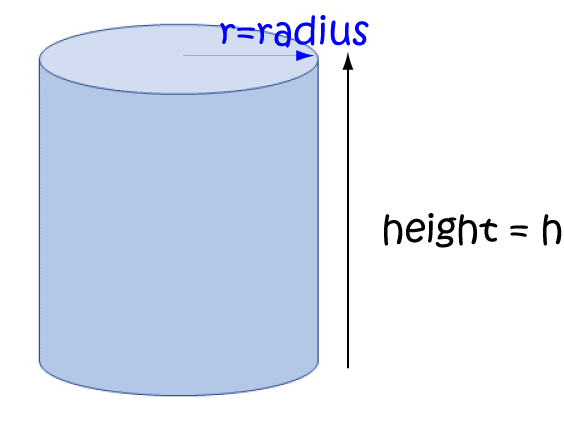
The volume of a cylinder is given by the formula \(V = \pi r^2 h\).
We can write this as a function of two variables:
\(V(r,h) = \pi r^2 h \)
Don't forget that \(\pi\) is a constant!
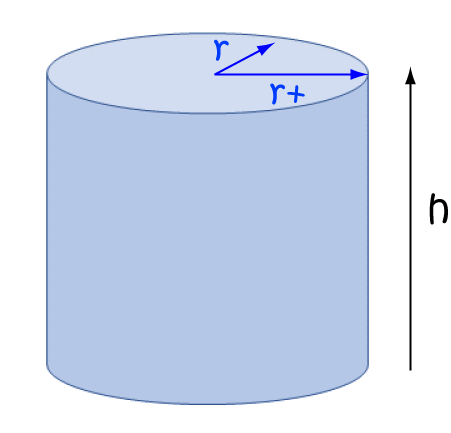
To find the partial derivative of \(V\) with respect to \(r\), we pretend that \(h\) is a constant, and allow \(r\) to vary. This gives:
\(V_r (r,h) = \pi (2r) h = 2 \pi rh \)
Don't forget that \(\pi\) is already a constant!
When we vary the radius by just a little bit, we increase the volume by adding a cylindrical shell of circumference \(2\pi r\) to the outside of the cylinder.
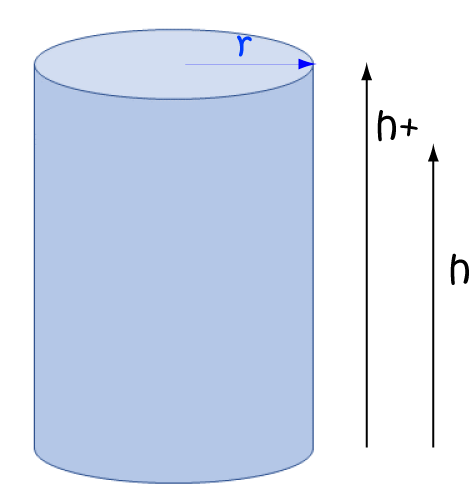
Now, what about the partial derivative of \(V\) with respect to \(h\)? We pretend that \(r\) is a constant, and allow \(h\) to vary. This gives:
\(V_r (r,h) = \pi r^2 (1) = \pi r^2 \)
Don't forget that \(\pi\) is already a constant!
When we vary the height by just a little bit, this is like increasing the volume by adding a circular disc of radius \(r\) to the top of the cylinder.
Time for another one?
Example:
The surface area of a square prism is given by the formula \(\text{SA} = 2\text{(Area Base)} + 4\text{(Area Sides)}\)
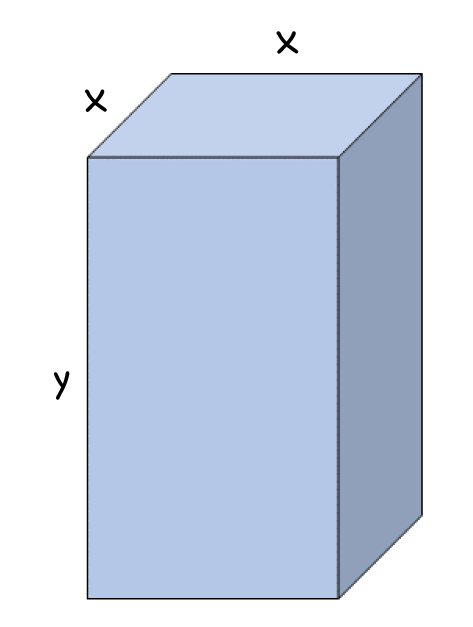
We can write the surface area as a function of the two variables \(x\) and \(y\). The area of the base is \(x^2\) and the area of each side is \(xy\). So the surface area is:
\(\text{SA}(x,y) = 2x^2 + 4xy \)
Now let's find our partial derivatives. Differentiate with respect to each variable individually, while holding the other one constant:
\( \begin{align*} \text{SA}_x(x,y)&= 2(2x) + 4(1)y = 4x + 4y\\ \text{SA}_y(x,y) &= 0 + 4x(1) = 4x \end{align*} \)
Now, what about the volume? The volume of a square prism is given by the formula \(\text{V} = \text{(Area Base)(Height)}\)
We can write the volume as a function of the two variables \(x\) and \(y\). The area of the base is \(x^2\) and the height is \(y\). So, the volume is:
\(\text{V}(x,y) = x^2y \)
Now let's find our partial derivatives. Differentiate with respect to each variable individually, while holding the other one constant:
\( \begin{align*} \text{V}_x(x,y)&= 2x(y) = 2xy\\ \text{V}_y(x,y) &= x^2(1) = x^2 \end{align*} \)
What if there are more variables?
You just hold 2 or more of them constant at a time, and focus your attention on differentiating with respect to only one of them.
Example:
Find the partial derivatives of the function \(f(x,y,z) = y^3 \sin (x) + x^2 \tan (y) + xy \cos(z)\).
To find \(f_x\), pretend that both \(y\) and \(z\) are constants, and differentiate with respect to \(x\):
\(f_x (x,y,z) = y^3 \cos(x) + 2x \tan(y) + (1)y\cos(z) = y^3 \cos(x) + 2x \tan(y) + y \cos(z) \)
To find \(f_y\), pretend that both \(x\) and \(z\) are constants, and differentiate with respect to \(y\):
\(f_y (x,y,z) = (3y^2) \sin (x) + x^2(\sec^2 (y)) + x(1)\cos(z) = 3y^2 \sin(x) + x^2 \sec^2(y) + x \cos(z) \)
Finally, to find \(f_z\), pretend that both \(y\) and \(z\) are constants, and differentiate with respect to \(z\):
\(f_y (x,y,z) = 0 + 0 + xy (-\sin(z)) = -xy \sin (z). \)
New wacky notation!
So far, we've used \(f_x\) to mean the partial derivative of \(f\) with respect to \(x\). There's another type of notation for partial derivatives that's very commonly used. We use a curly "d" (\(\partial\)) as follows:
\(\dfrac{\partial f}{\partial x} = f_x \).
We pronounce \(\partial\) as "del" or "dee" or "curly dee", and so we might say \(\dfrac{\partial f}{\partial x}\) as "curly dee f curly dee x".
Back to Sid
Sid wants to know about his rates of consumption of leaves in the \(x\) and \(y\) directions. His leaf consumption formula is:
\(\text{leaves}(x,y) = 3x^2 + 2xy,\)
and we need to find his rates of consumption in both directions at the point \((2,3)\) on the wall.
Let's start by finding the partial derivatives:
\( \begin{align*} \dfrac{\partial \text{leaves}}{\partial x} &= 6x + 2y\\ \dfrac{\partial \text{leaves}}{\partial y} &= 0 + 2x = 2x \end{align*} \)
Next, evaluate the partial derivatives at the point \(2,3\):
\( \begin{align*} \dfrac{\partial \text{leaves}}{\partial x} &= 6(2) + 2(3) = 18 \text{ leaves/cm}\\ \dfrac{\partial \text{leaves}}{\partial y} &= 2(3) = 6 \text{ leaves/cm}. \end{align*} \)
So, Sid appears to be consuming leaves more rapidly in the \(x\)-direction.
Description
Calculus is the branch of mathematics that deals with the finding and properties of derivatives and integrals of functions, by methods originally based on the summation of infinitesimal differences. The two main types are differential calculus and integral calculus.
Environment
It is considered a good practice to take notes and revise what you learnt and practice it.
Audience
Grade 9+ Students
Learning Objectives
Familiarize yourself with Calculus topics such as Limits, Functions, Differentiability etc
Author: Subject Coach
Added on: 23rd Nov 2017
You must be logged in as Student to ask a Question.
None just yet!