Calculus
Chapters
Maxima and Minima with Calculus
Maxima and Minima with Calculus
Introduction
 Let's start by thinking about a useful real
world problem that you probably won't find in your maths
textbook.
Let's start by thinking about a useful real
world problem that you probably won't find in your maths
textbook.
Alice the cow is a bit of a thrill-seeker. She's decided to try spring-board diving down at the farmyard's dam, and wants to know just how high she'll be able to jump.
Alice has worked out that her height at time \(t\) seconds after she jumps on the spring-board will be given by the equation \(\text{bounce}(t) = -\dfrac{4}{9}\;t^2 + \dfrac{24}{9}\;t + 10 \text{ m}\). What is the maximum height that Alice will reach?
So, to find out how high she will jump, Alice needs to find a local maximum of the function \(\text{bounce}(t)\). One way to do this is using calculus. Let's find out how. We'll start out with another example, and come back to Alice later.
Example
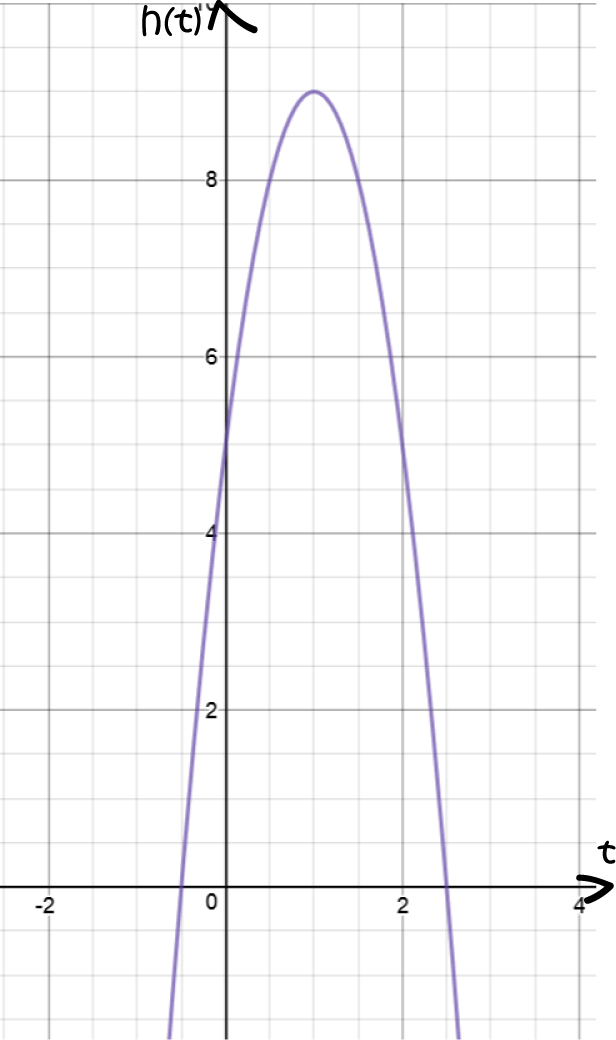
What is the maximum height reached by the rocket?
We start by using derivatives to find the slope of the function:
(In case you've forgotten, there's a quick refresher course on finding derivatives after this example)
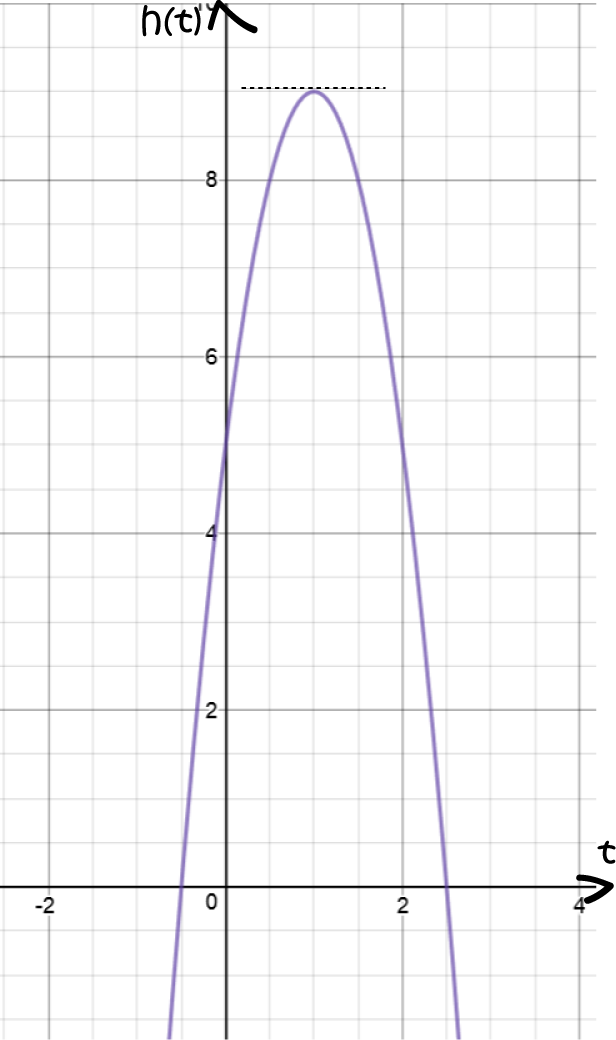
Next, we need to work out when the slope is zero:
Finally, we need to find the maximum height of the rocket. Plug \(t = 1\) into the formula for \(h(t)\). Be careful that you don't try to plug it into the equation for the derivative, \(h'(t)\):
A Quick Review of Derivatives
Derivatives are, essentially, the slopes of functions.
In our example, we started with the function:
We did this by using the following rules of derivatives:
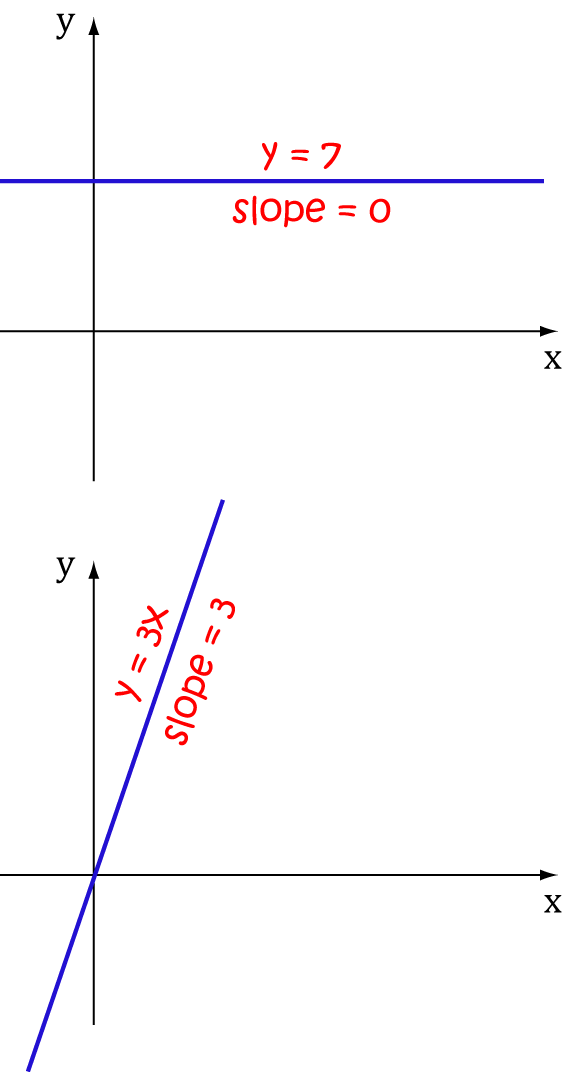
- The slope of a horizontal line like \(y = 7\) is always zero. So, the slope of \(5\) is zero.
- The slope of a line like \(y = 3x\) is \(3\). The slope of the line \(y = mx + b\) is \(m\). So, the slope of \(8t\) is \(8\).
- A square function like \(x^2\) has a slope of \(2x\). So, the slope of \(-4t^2\) is \(-4(2t) = -8t\).
Then we used the sum and difference rules to add them together to give:
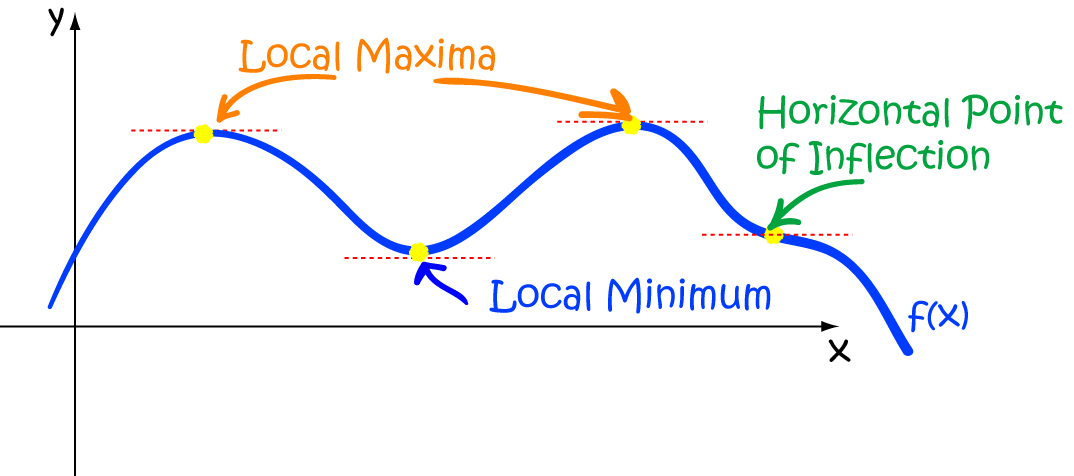
Working Out Whether It's a Maximum or Minimum
In our example, we were able to work this out from the graph, but this isn't always possible.
If the graph isn't going to work, there are two options
that will help you out. Both involve derivatives. Funnily
enough, the first one is called the First
Derivative Test (not because it's the first test
involving derivatives, but because it uses the first
derivative!)
The First Derivative Test
In the First Derivative Test, we look at the values of the first derivative, either side of the point where the derivative is zero:
- If the slope is positive to the left and negative to the right of the point where the slope is zero, we have a local maximum
- If the slope is negative to the left and positive to the right of the point where the slope is zero, we have a local minimum
- If the slope does not change sign either side of the point where the slope is zero, we may have a horizontal point of inflection
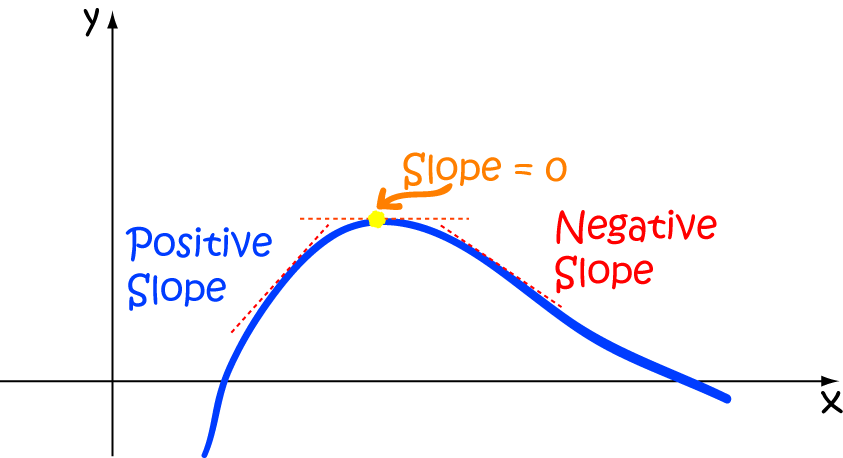
In the picture above, the yellow dot is a local maximum.
The other test is called the Second Derivative
Test, and you guessed it, it involves the second
derivative.
The Second Derivative Test
The second derivative tells us about the concavity of a function. If you'd like to know more, you can read the article about concavity. The second derivative test relies on the fact that a function with a positive second derivative is concave up, and a function with a negative second derivative is concave down. So, to perform the second derivative test, we evaluate the second derivative of the function at the points \(x\) where the function has slope zero:
- If the second derivative at \(x\) is negative, then the function has a local maximum at \(x\)
- If the second derivative at \(x\) is positive, then the function has a local minimum at \(x\)
- If the second derivative at \(x\) is zero, then we're in trouble! The test fails, and we need to go back to the first derivative test.
Let's try this out on an example.
Example
Find the maxima and minima of the function
Start by finding where the slope is zero:
As these zeroes look pretty horrible, we'll use the second derivative test. The second derivative is \(\dfrac{d^2y}{dx^2} = 24x + 6\).
At \(x = 0.2287\), \(\dfrac{d^2y}{dx^2} \approx 11.4888 > 0\). So, we have a local minimum here.
At \(x = -0.7287\), \(\dfrac{d^2y}{dx^2} \approx - 11.4888 < 0\). So, we have a local maximum here.
We should really plug these values into the equation for \(y\) to see what the corresponding \(y\)-values are. Feel free to do that!
OK, let's look at the graph and see if we're right:
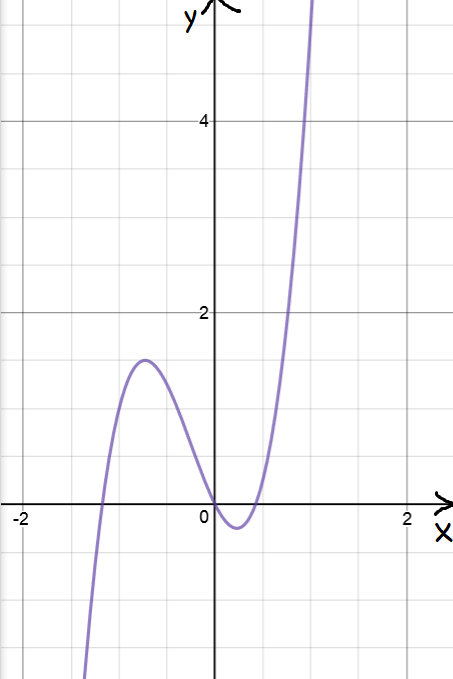
It looks pretty good to me, what do you think?
Now it's time to deal with our spring-boarding cow.
Example
You might recall that Alice the cow was determined to try spring-board diving down at her local dam and wanted to know how high she could jump.
Her height at time \(t\) seconds after jumping on the spring-board was given by the equation:
Let's differentiate it to see if we can figure out where this equation has a local maximum:
Let's check this one using the first derivative test:
- If \(t < 3\), say \(t = 2.5\), then \(\text{bounce}'(t) \approx 0.4444 > 0\), so the function is increasing.
- If \(t > 3\), say \(t = 3.5\), then \(\text{bounce}'(t) \approx -0.4444 < 0\), so the function is decreasing.
Let's do one more example to see what can go wrong with the second derivative test:
Example
Find the maxima and minima of \(y = x^3 - 6x^2 + 12 x - 7\).
Differentiating gives
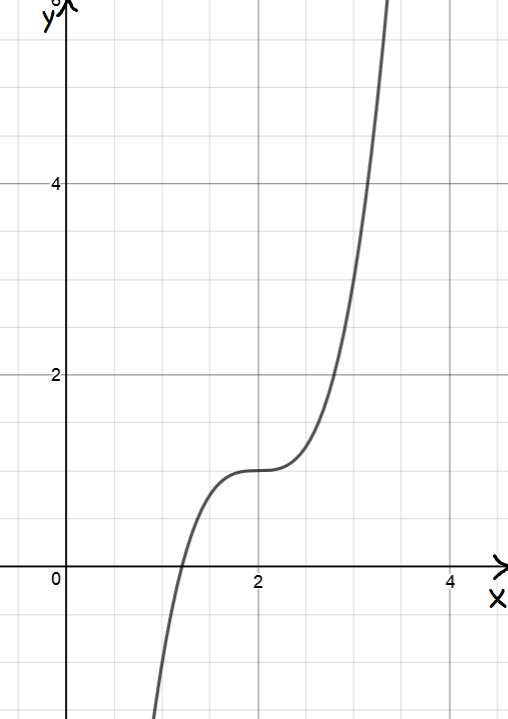
To use calculus to find local maxima and minima, the function must be differentiable
Calculus falls down miserably as a technique for finding local maxima and minima if the function is not differentiable.
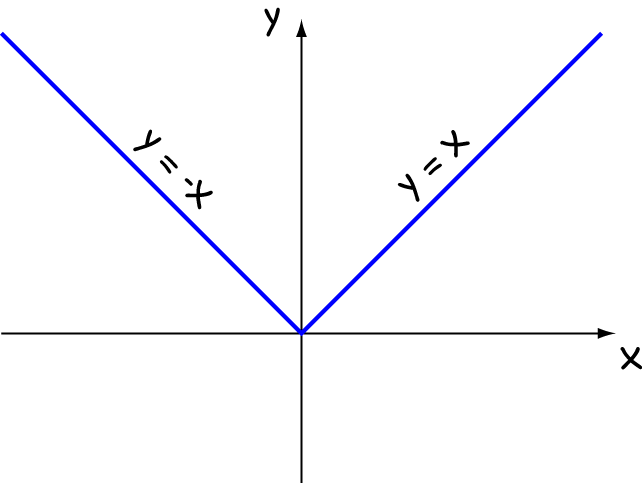
For example, let's look at the absolute value function, \(f(x) = |x|\). Just a quick reminder...
If we look at the graph of \(f(x)\) (see below), we can see that there's a local minimum at \(x = 0\):
Recap on Terminology
- A high point of a function is called a maximum (maxima in plural)
- A low point of a function is called a minimum (minima in plural)
- We call all the maxima and minima of a function its extrema when we talk about them together
- We refer to local maxima or local minima when the function has higher or lower values away from the extrema.
Description
Calculus is the branch of mathematics that deals with the finding and properties of derivatives and integrals of functions, by methods originally based on the summation of infinitesimal differences. The two main types are differential calculus and integral calculus.
Environment
It is considered a good practice to take notes and revise what you learnt and practice it.
Audience
Grade 9+ Students
Learning Objectives
Familiarize yourself with Calculus topics such as Limits, Functions, Differentiability etc
Author: Subject Coach
Added on: 23rd Nov 2017
You must be logged in as Student to ask a Question.
None just yet!