Triangles

A triangle is a plane (flat) shape with straight edges. It has

• Three edges and
• Three angles.

The three angles of a triangle always add up to \(180^\circ\). We say that the angle sum of a triangle is equal to \(180^\circ\).

Special Types of Triangles

Based on the Number of Equal Sides (or Angles)

There are three names that we give to triangles that have certain numbers of equal sides (or angles). They are

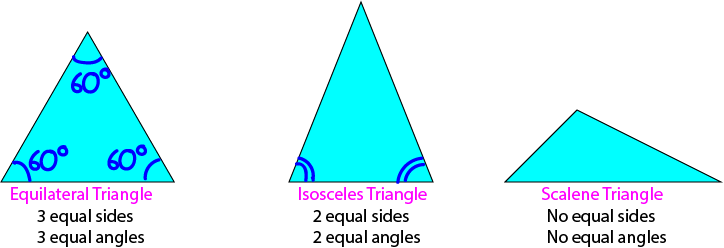
All three sides of an equilateral triangle have the same length. This means that all three angles of an equilateral triangle have the same size. Since the angle sum of a triangle is \(180^\circ\), all three angles of an equilateral triangle must be \(60^\circ\).

Two sides of an isosceles triangle have the same length. These two sides are opposite two angles which must also have the same size.

In a scalene triangle, nothing is the same. All of its sides have different lengths, and all of its angles have different sizes.

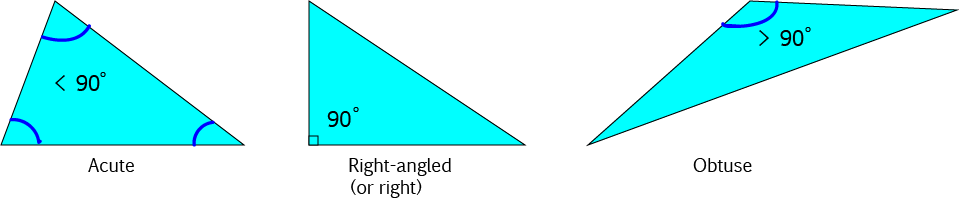
Based on the Sizes of Angles

In an acute triangle, all angles must be smaller than \(90^\circ\).

In a right-angled triangle (also known as a right triangle), one angle is a right angle (\(90^\circ\)).

In an obtuse triangle, one angle is bigger than \(90^\circ\). Only one angle can be bigger than \(90^\circ\) because the angle sum of a triangle is \(180^\circ\).

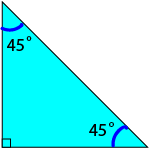
Two Things at the Same Time

All equilateral triangles are acute because all of their angles are \(60^\circ\) and \(60^\circ

However, we can talk about a right isosceles triangle. This is an isosceles triangle in which one of the angles is \(90^\circ\). Because an isosceles triangle has two equal angles, the other two angles must both be \((180^\circ - 90^\circ) \div 2 = 45^\circ\).

Perimeter of a Triangle

The perimeter of a triangle is the distance you would cover if you walked around the triangle, along its edges once. You find it by adding up the lengths of the three sides of the triangle.

Example

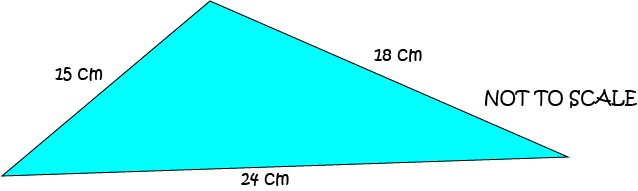
Find the perimeter of the triangle in the picture.

Solution:

The perimeter is the sum of the lengths of the sides of the triangle:

\( P = 15 + 18 + 24 = 57 \text{ cm} \)

Area of a Triangle

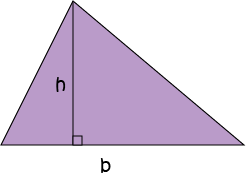
The area of a triangle is given by the formula

\( A = \dfrac{1}{2}\;bh, \)

where \(b\) is the length of the base of the triangle, and \(h\) is the height of the triangle (which is measured at right angles to the base).

Note: You can choose the base to be any side of the triangle, just so long as you take the height to be at right angles to the base.

Why Does it Work?

Every triangle is half of a parallelogram:

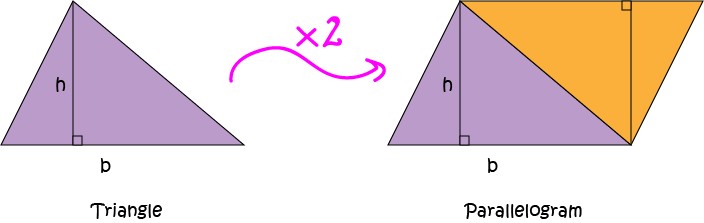
Since the area of a parallelogram is equal to the base of the parallelogram times the height, the area of a triangle is equal to half of this amount:

Example

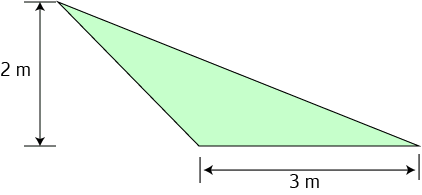
Find the area of the triangle in the picture.

Solution:

The area is equal to half the base times the height, so:

\( A = \dfrac{1}{2}\; (3)(2) = 3 \text{ m}^2 \)