Year 10+ Plane Geometry
Chapters
3-4-5 Triangle
3-4-5 Triangle
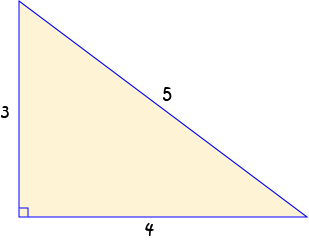
A 3-4-5 triangle is a triangle with sides of length 3 units, 4 units and 5 units.
What's special about these side lengths? I'm glad you asked...
Any triangle with side lengths of 3 units, 4 units and 5 units is guaranteed to be a right-angled triangle.
Constructing a 3-4-5 Triangle
This is a ruler and compass construction. We have to cheat a bit by measuring a few things, so it isn't quite a straight edge and compass construction.
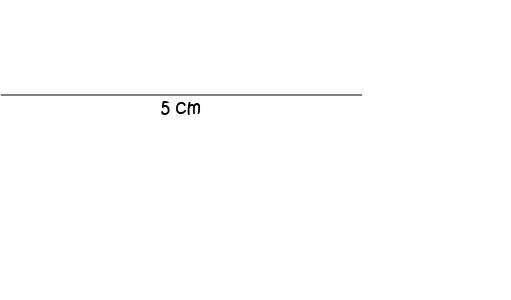
Start off by drawing a line segment that's \(5\) cm long. Don't be like Sam (you should see the mess he makes)! Use a ruler.
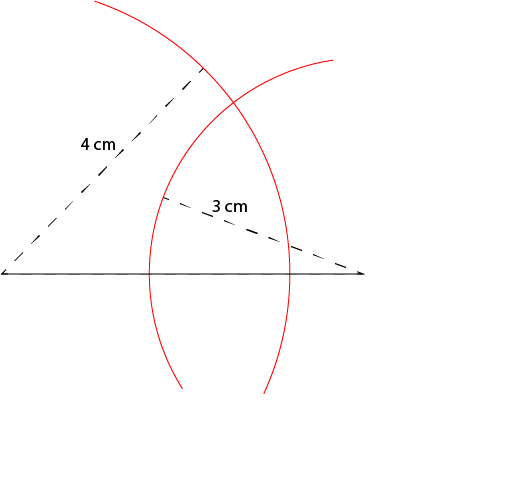
Open out your compass to a radius of 4 centimetres. Stick the tip in at one end of your line segment and draw an arc. Make it nice and long so that it will intersect with the arc that you draw next.
Next, open your compass to a radius of 3 centimetres. Stick the tip in at the other end of your line segment and draw a second arc. Make it long enough to intersect with the first arc you drew.
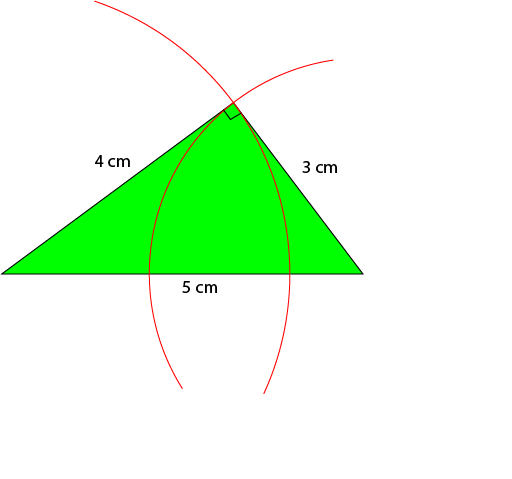
Now you're ready to draw the sides of your triangle. Use your ruler to join up each end of the line segment to the point where the arcs intersect. The right angle will be between the two sides that you just formed. You have created your own, beautiful (if you used a ruler!), 3-4-5 triangle.
Are There Any Other Side Lengths That Work?
The Easy Answer
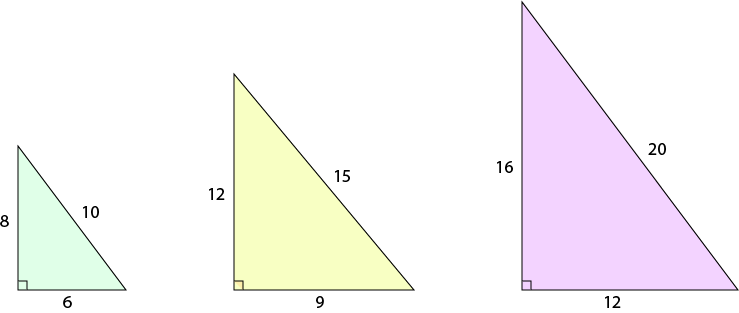
Yes! Any multiples of 3, 4, and 5 (the same multiple for each) will work. So there are right-angled 6-8-10, 9-12-15, 12-16-20, 3,000-4,000-5,000 triangles, and triangles with sides that are any other multiple of 3, 4, and 5 that you care to think of.
Here are some of them:
What About Sets of Sides that Aren't Multiples of 3,4, and 5?
Well, now things get more complicated, but the answer is still yes. First, we need to understand why 3,4, and 5 works.
Pythagoras' Theorem
Pythagoras' Theorem states that
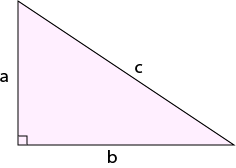
In a right-angled triangle, the sum of the squares of the shorter sides (\(a^2 + b^2\)) is equal to the square of the longer side (\(c^2\)).
Pythagoras' theorem also works in reverse: if the sum of the squares of the shorter sides of a triangle is equal to the square of the longer side of the triangle, then the triangle is right angled.
Let's check out our 3-4-5 triangle:
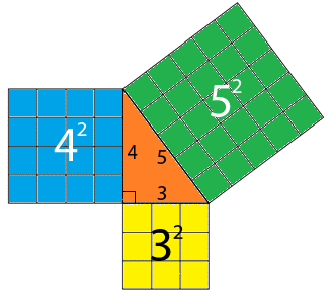
For the 3-4-5 triangle,
So, yes, it works and our 3-4-5 triangle is right angled.
So What About Those Other Side-Lengths
There are infinitely many of them! Any three positive numbers \(a, b\) and \(c\) that satisfy \(a^2 + b^2 = c^2\) will give you a right-angled triangle. We call a set of three numbers satisfying this
equation a Pythagorean Triad.
Here are a few more examples:

Let's test them out:
- The 8-15-17 triangle:
\( \begin{align*} 8^2 + 15^2 &= 64 + 225\\ &= 289\\ &= 17^2 \end{align*} \)So this one is right-angled.
- The 11-60-61 triangle:
\( \begin{align*} 11^2 + 60^2 &= 121 + 3,600\\ &= 2,721\\ &= 61 \end{align*} \)So this one is right-angled too.
- Why not check the 7-24-5 triangle yourself?
Description
In these chapters you will learn about plane geometry topics such as
- Area (Irregular polygons, plane shapes etc)
- Perimeter
- Conic sections (Circle, Ellipse, Hyperbola etc)
- Polygons (Congruent, polygons, similar, triangles etc)
- Transformations and symmetry (Reflection, symmetry, transformations etc)
etc
Even though these chapters are marked for Year 10 or higher students, several topics are for students in Year 8 or higher
Audience
Year 10 or higher, suitable for Year 8 + students as well.
Learning Objectives
Learn about Plane Geometry
Author: Subject Coach
Added on: 28th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!