Circle Sectors and Segments

Bits of a Circle

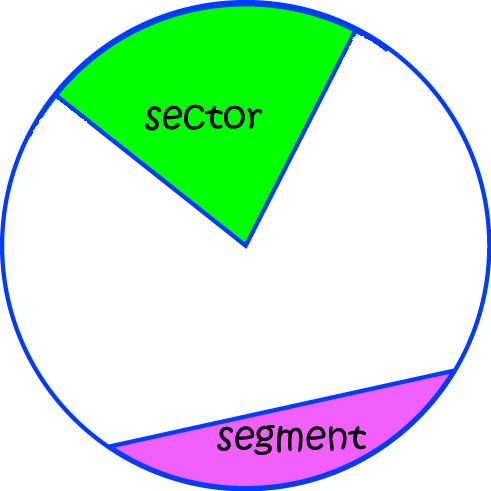
There are two main parts of a circle that we are interested in:

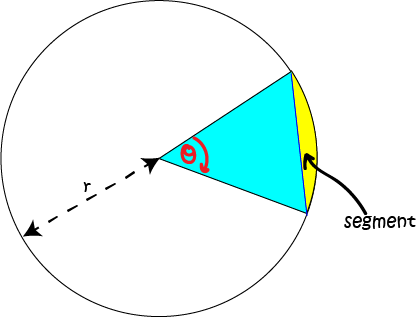
• A sector is shaped like a slice of cake - it's wedge-shaped and continues all the way out from the centre of the circle to the circumference.
• A segment is a bit cut off the circle by a chord (a line that joins two points on the circumference of the circle).

Semicircles and Quadrants

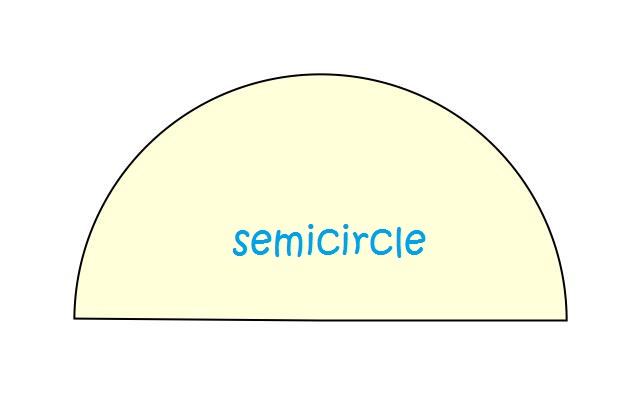
A semicircle is half of a circle. It is the sector which forms an angle of \(180^\circ\) (or \(\pi \text{ radians}\)) at the centre of the circle.

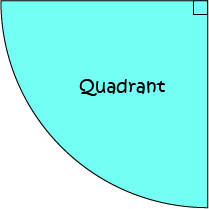
A quadrant is a quarter of a circle. It is the sector which forms an angle of \(90^\circ\) (or \(\dfrac{\pi}{2} \text{ radians}\)) at the centre of the circle.

Areas of Sectors

The area of a sector depends on the angle it forms at the centre of the circle. The angle helps you to figure out what fraction of the circle is taken up by the sector.

At present, we'll measure our angles in radians as it makes the calculations easier.

There are \(2\pi\) radians in a full revolution. We can think of a whole circle as a sector with angle \(2\pi \text{ radians}\) at the centre.

We know the formula for the area of the circle. It's \(\pi r^2\), where \(r\) is the radius of the circle.

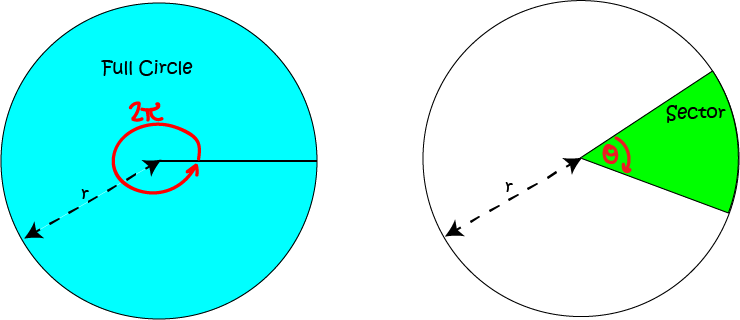
If a sector forms an angle of \(\theta \text{ radians}\) at the centre of the circle, then its area will be equal to \(\dfrac{\theta}{2\pi}\) of the area of the circle. So, the formula for the area of the sector is given by

If you have to work in degrees, we'll need to adjust this formula a little. Remember that (\(180^\circ = \pi \text{ radians}\)). So, the formula becomes

Example

A circle has radius \(3 \text{ cm}\). Find the area of a sector with central angle \(\dfrac{\pi}{6}\) radians.

Solution:

The area is given by the formula \(A = \dfrac{1}{2}r^2 \theta\), where \(\theta\) is the central angle in radians. In this example, \(r = 3\) cm and \(\theta = \dfrac{\pi}{6}\), so the area is \(A = \dfrac{1}{2} 3^2 \times \dfrac{\pi}{6} = \dfrac{9\pi}{12} = \dfrac{3\pi}{4} \text{ cm}^2\).

Area of a Segment

To find the area of a segment, we start with the area of a sector, and subtract the area of a triangle whose three sides are formed by 2 radii of the circle and the chord cutting off the segment.

You might recall from your trigonometry studies that the area of a right angle with sides \(a\) and \(b\) and included angle \(\theta\) is given by \(\dfrac{1}{2}ab \; \sin (\theta)\). If not, it is! So, if \(\theta\) is measured in radians, the area of the segment is equal to

\( A = \dfrac{1}{2} r^2 \theta - \dfrac{1}{2} r^2 \sin \theta = \dfrac{1}{2}r^2 (\theta - \sin (\theta))\)

If \(\theta\) is measured in degrees, then we need to adjust this as for the area of a sector to given

\( A = \dfrac{1}{2} r^2 \left(\dfrac{\theta \times \pi}{180} - \sin (\theta)\right)\)

Example

A circle has radius \(3 \text{ cm}\). Find the area of a segment with central angle \(\dfrac{\pi}{6}\) radians.

Solution:

The area is given by the formula \(A = \dfrac{1}{2}r^2 (\theta - \sin (\theta))\), where \(\theta\) is the central angle in radians. In this example, \(r = 3\) cm and \(\theta = \dfrac{\pi}{6}\), so the area is \(A = \dfrac{1}{2} 3^2 \left( \dfrac{\pi}{6} - \sin \dfrac{\pi}{6}\right) \approx 0.106 \text{ cm}^2\).

Arc Length

The arc length depends on the angle it subtends at the centre of the circle. The angle helps you to figure out what fraction of the circle's circumference is taken up by the arc.

At present, we'll measure our angles in radians as it makes the calculations easier.

There are \(2\pi \) radians in a full revolution. We can think of a whole circle as a sector with angle \(2\pi \text{ radians}\) at the centre.

We know the formula for the circumference of the circle. It's \(2\pi r\), where \(r\) is the radius of the circle.

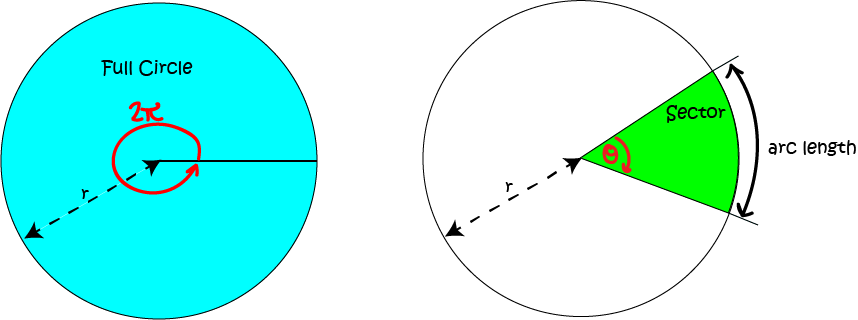
If the arc subtends an angle of \(\theta \text{ radians}\) at the centre of the circle, then its length will be equal to \(\dfrac{\theta}{2\pi}\) of the circumference of the circle. So, the formula for the arc length is given by

If you have to work in degrees, we'll need to adjust this formula a little. Remember that (\(180^\circ = \pi \text{ radians}\)). So, the formula becomes

Example

A circle has radius \(3 \text{ cm}\). Find the length of an arc that subtends an angle of \(\dfrac{\pi}{6}\) radians at the centre of the circle.

Solution:

The arc length is given by the formula \(A = r \theta\), where \(\theta\) is measured in radians. In this example, \(r = 3\) cm and \(\theta = \dfrac{\pi}{6}\), so the arc length is \(L = r \theta = 3 \times \dfrac{\pi}{6} = \dfrac{\pi}{2} \text{ cm}\).