Year 10+ Plane Geometry
Chapters
Congruent Triangles
Congruent Triangles
Two triangles are congruent if they have three pairs of equal side lengths and three pairs of equal angles.
Congruent
Things that arecongruent look exactly the same. We say that a shape is congruent to another shape if it can be turned into
the other shape by using one, two or all three of sliding, flipping and turning. Let's see what each of these moves does to a shape.
Slides, Flips and Turns
Slide: In this move, the object is pushed along (without changing the lengths of any of its lines or the directions they point in)
to another place.
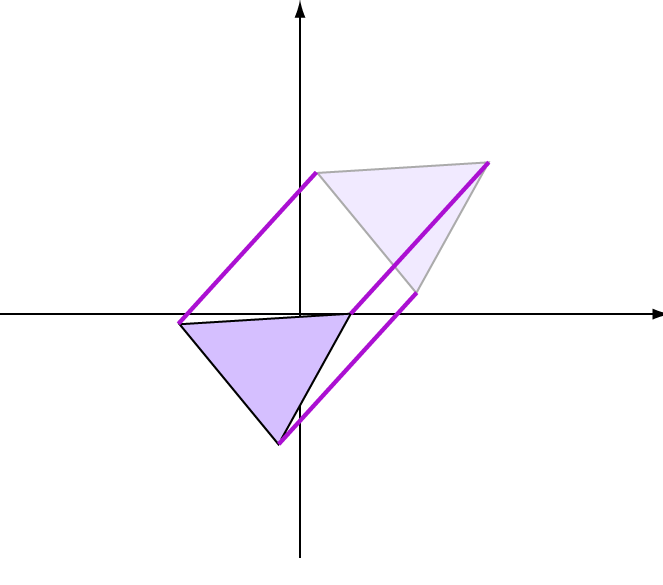
translation.
Flip: this is like looking at the object in the mirror. You can flip in different directions by putting the mirror in different places. The object is still the same
size and shape after it has been flipped, just backwards somehow.
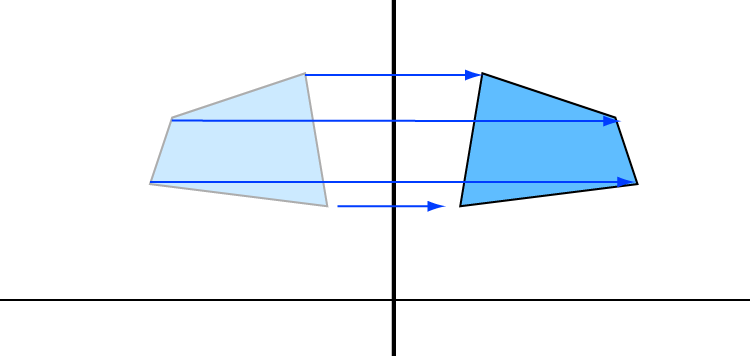
reflection.
Turn: this is spinning the object. Pick a point either inside or outside the object and spin the object around that point. If the point is outside the object, it's like
spinning a tennis ball around in a stocking. If the point is inside the object, it's like sticking a pin in the object and spinning it around that point like a wheel spins around its axle.
The object is still the same size and shape after it has been turned.
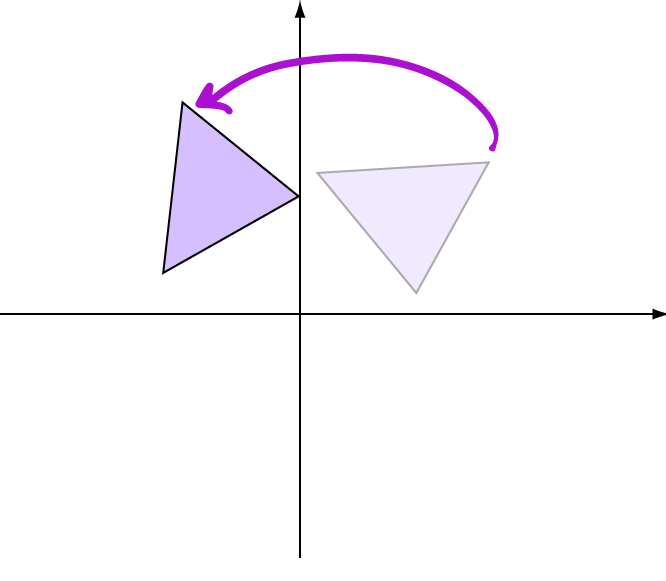
rotation.
Congruent Triangles
Two triangles are congruent if they have three pairs of equal side lengths and three pairs of equal angles.
The sides and angles might appear to be in different positions if a turn or a flip has been used to turn one triangle into the other, but they will all be equal.
Triangles with All Sides Equal
If two triangles have three pairs of equal sides, then they are automatically congruent.
For example,

Triangles with All Pairs of Angles Equal
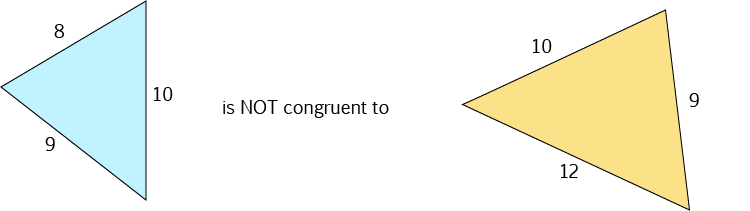
If two triangles have three pairs of equal angles, they may or may not be congruent. It depends on whether they have the same size.
For example,
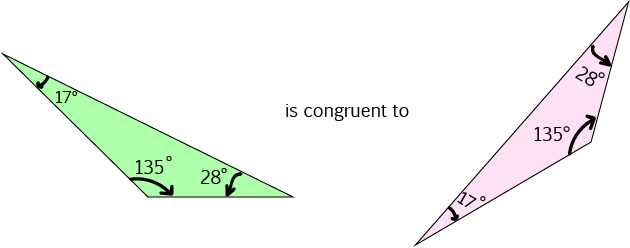
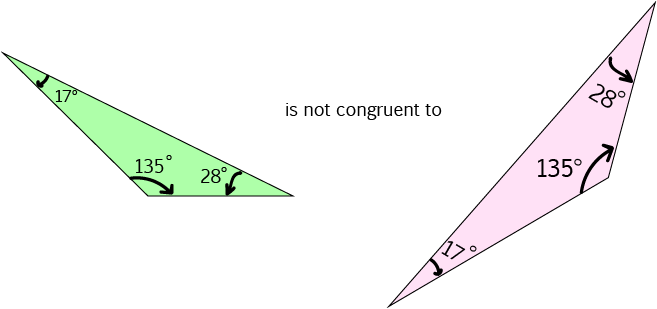
If two triangles have three pairs of equal angles, then they are similar, but they may not be congruent.
Other Tests for Congruent Triangles
There are a number of other tests for congruent triangles. For example, two right angled triangles are congruent if their hypotenuses are equal, and one other pair of sides is equal. Another test is to show that they have two pairs of sides and the pair fo included angles equal.
You can read more about these tests in the article on proving that triangles are congruent.
How Do We Indicate That Two Triangles are Congruent?
We use markings to show which pairs of sides are equal and which pairs of angles are equal. For example,

In the above picture, we've shown the pairs of equal angles using different numbers of arcs: the angles with single arcs are equal, the angles marked with double arcs are equal, and the angles marked with triple arcs are equal. We've also marked the equal sides using different symbols: one pair of equal sides has single lines, another has double lines, and a third has a curvy symbol.
Of course there are many other ways you can show that two triangles are congruent. In symbols, we write \(ABC \equiv DEF\) to say that triangles \(ABC\) and \(DEF\) are congruent. It's usually a good idea to put the vertices in the order corresponding to the pairs of equal angles. We'll talk more about that in the article on proving that triangles are congruent.
Description
In these chapters you will learn about plane geometry topics such as
- Area (Irregular polygons, plane shapes etc)
- Perimeter
- Conic sections (Circle, Ellipse, Hyperbola etc)
- Polygons (Congruent, polygons, similar, triangles etc)
- Transformations and symmetry (Reflection, symmetry, transformations etc)
etc
Even though these chapters are marked for Year 10 or higher students, several topics are for students in Year 8 or higher
Audience
Year 10 or higher, suitable for Year 8 + students as well.
Learning Objectives
Learn about Plane Geometry
Author: Subject Coach
Added on: 28th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!