Year 10+ Plane Geometry
Chapters
Conic Sections
Conic Sections
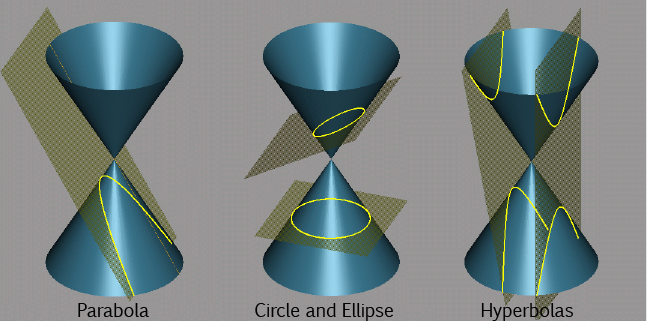
Did you know, that when you take slices through a cone at different angles, you get cross-sections shaped like circles (slicing parallel to the base), ellipses
(slicing at a slight angle to the base), parabolas (slicing parallel to the edge of the cone) and hyperbolas (slicing at a steep angle to the base)? We call all of
these curves conic sections because they're obtained by taking different cross-sections of a cone.
Focus, Directrix and Eccentricity
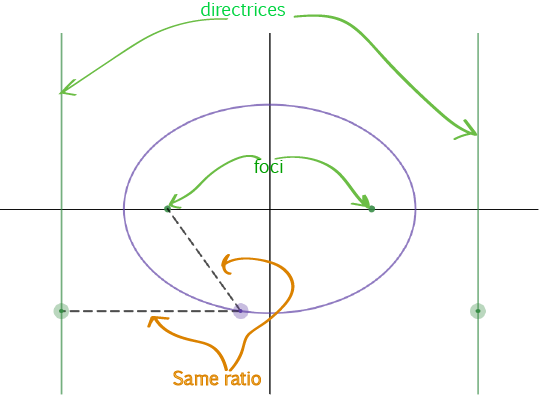
We can also define these curves as the sets of points satisfying a condition that involves a straight line (or two) called the directrix (or directrices)
and a point (or two) called the focus (or foci). Ellipses and Hyperbolas have two foci and two directrices. Parabolas have only one.
The points on a conic section move so that the ratio between the
- Distance from the point to one focus and the
- Perpendicular distance from the point to one directrix
- For ellipses, the ratio between these distances is always less than one.
- For parabolas, the ratio is always equal to one. The two distances are always equal.
- For hyperbolas, the ratio is always greater than one.
We call this ratio the eccentricity \(e\) of the conic section. The circle has eccentricity zero. So, the eccentricity measures how far the conic section
is from being a circle. Less curvy conics have larger eccentricities.

Different types of conic sections have different eccentricities:
- All circles have \(e=0\)
- The eccentricity of ellipses varies: \(0 .
- All parabolas have \(e = 1\).
- Hyperbolas all have \(e > 1\).
- Being as uncurved as you can get, straight lines have infinite eccentricity.
Latus Rectum
It sounds a bit like an unmentionable body part, doesn't it? It isn't! The latus rectum is a line passing through the focus of a conic that is parallel to the
directrix, and joins two points of the conic. In a circle, the latus rectum is a diameter.
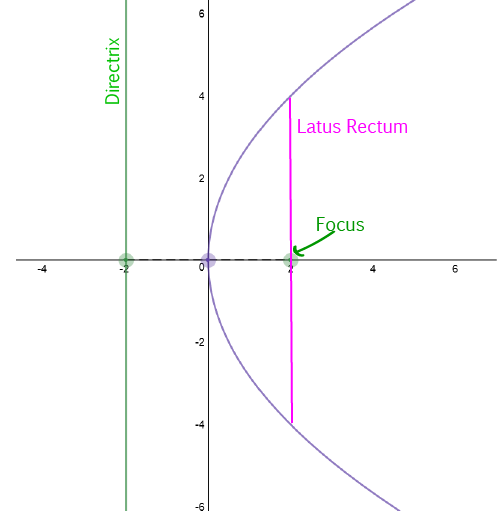
In a parabola, the length of the latus rectum is equal to four times the focal length (the distance from the focus to the vertex).
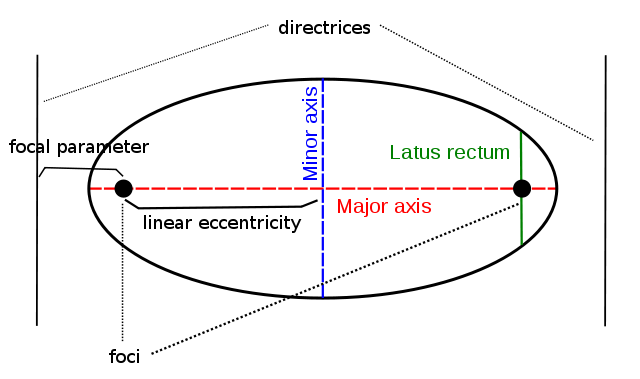
An ellipse has two latus recta (the plural of latus rectum) because it has two foci and two directrices.
The length of the latus rectum is equal to \(\dfrac{2b^2}{a}\), where \(a\) is half the length of the major axis and \(b\) is half the length of the minor axis.
General Equation of a Conic Section
We can plot all conic sections in the \(xy\)-plane: cross-sections of a solid are 2-dimensional.
The equation involves terms in
- \(x^2\)
- \(y^2\)
- \(xy\)
- \(x\) and \(y\)
- A constant term
Different coefficients will turn the equation into the equation of a circle, an ellipse, a parabola or a hyperbola.
The general equation is:
For example, this is the graph of
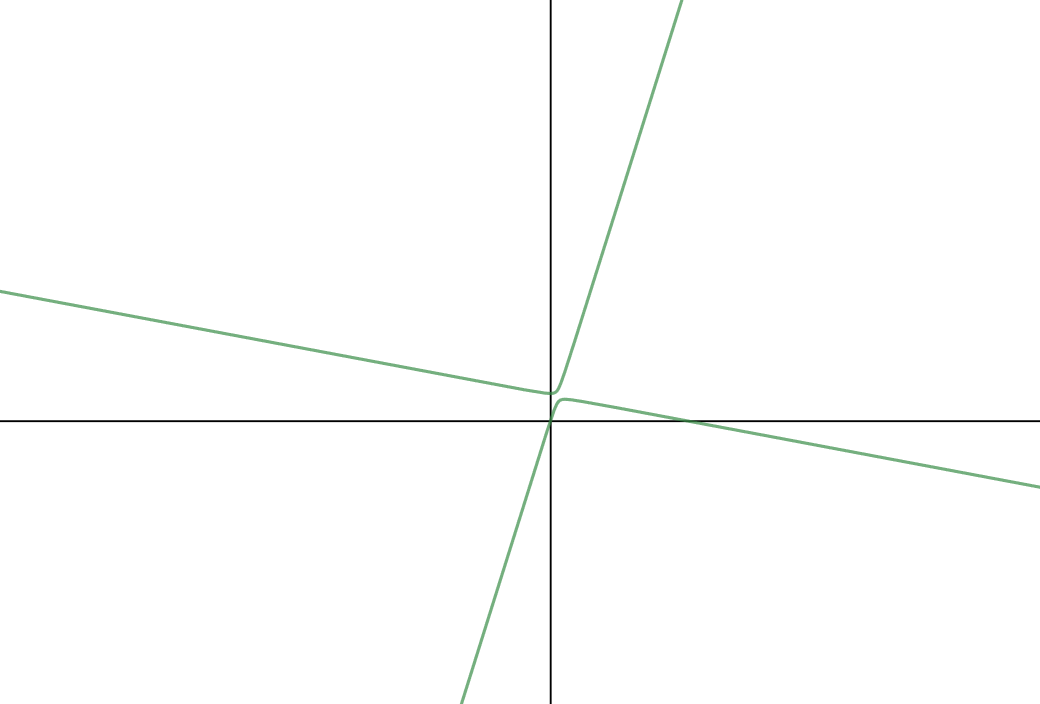
We'll explore which values give which conics in the articles on the individual types of conic sections. In the mean time, why not have a play around on an on-line graphing calculator with different values of \(A, B, C, D, E, \) and \(F\)? Don't forget to try negative values as well. Have fun!
Description
In these chapters you will learn about plane geometry topics such as
- Area (Irregular polygons, plane shapes etc)
- Perimeter
- Conic sections (Circle, Ellipse, Hyperbola etc)
- Polygons (Congruent, polygons, similar, triangles etc)
- Transformations and symmetry (Reflection, symmetry, transformations etc)
etc
Even though these chapters are marked for Year 10 or higher students, several topics are for students in Year 8 or higher
Audience
Year 10 or higher, suitable for Year 8 + students as well.
Learning Objectives
Learn about Plane Geometry
Author: Subject Coach
Added on: 28th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!