Showing Triangles are Similar

We've talked about similar objects before. Similar objects look the same, but they might have different sizes. You can turn a geometric shape into a similar shape by performing one or more of the transformations: rotation, reflection, translation and enlargement.

If two triangles are similar then

• They have three pairs of equal angles
• They have three pairs of corresponding sides, with lengths in the same ratio.

If we want to prove that two triangles are similar, we don't need to check all six of these things. There are some theorems that can cut down on the amount of work we need to do. We can show that two triangles are similar by verifying that one of the following things are satisfied:

1. All three pairs of their angles are equal. Some people call this property equiangular. Other people abbreviate it by AAA for angle-angle-angle.
2. The lengths of all three pairs of corresponding sides are in the same ratio. This is often abbreviated as SSS for side-side-side.
3. The lengths of two pairs of corresponding sides are in the same ratio, and the included angles are equal. This is often abbreviated as SAS for side-angle-side.

Let's look at some examples where each of these tests for similarity can be applied.

Equiangular Triangles are Similar

To prove that all three pairs of angles are equal, you really only need to prove that two pairs of angles are equal. The angle sum of a triangle (always \(180^\circ\)) will ensure that the third pair are equal.

Note: A few years ago, someone made a bit of a fuss in NSW about people using AAA as the abbreviation for this test. I don't know what the current thinking is, but it's probably safer to refer to this test as the "equiangular" property in NSW. It's best to check your textbooks for the appropriate abbreviation to use in other states.

This test says that if two triangles have all three pairs of their angles equal, then they are similar.

Example

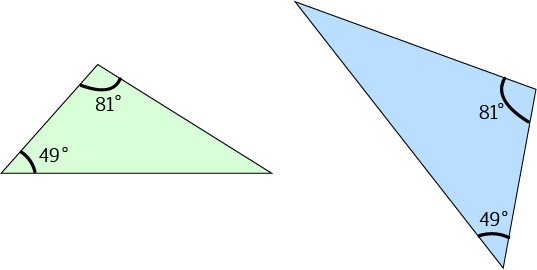
The two triangles on the left are similar because all three pairs of their angles are equal. Two pairs of equal angles are marked (the \(49^\circ\) and the \(81^\circ\) angles). The remaining pair of angles must both be equal to \(180 - 49 - 81 = 50^\circ\) since the angles of a triangle always add up to \(180^\circ\).

It isn't necessary, but if you wanted to prove that the three pairs of sides of these triangles were in the same ratio, you could use the sine rule. See the article on the sine rule for more information.

Two Pairs of Sides (in the same ratio) and the Included Angle (equal)

We often abbreviate this test by SAS (short for side-angle-side)

This test says that two triangles in which two pairs of corresponding sides are in the same ratio, and the angles included by those sides are equal, are similar.

Let's apply it to an example.

Example

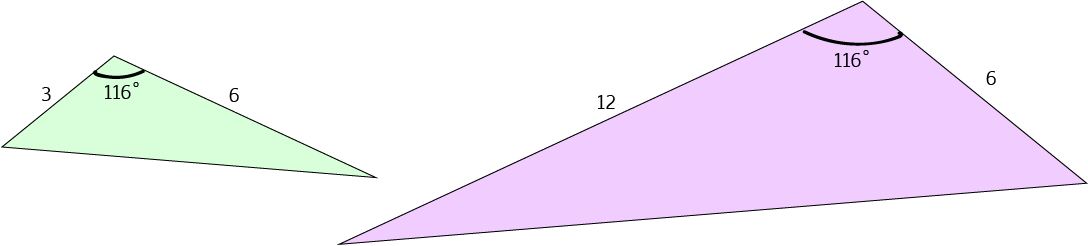
In the green and mauve triangles on the left:

• The longest pair of marked sides are in the ratio \(6:12 = 1:2\) (green:mauve)
• The shortest pair of marked sides are in the ratio \(3:6 = 1:2\) (green:mauve)
• The angles between the marked sides are both equal to \(116^\circ\)

So, the two triangles are similar by the side-angle-side (SAS) test.

It isn't necessary, but if you wanted to prove that the three pairs of sides of these triangles were in the same ratio, you could use the cosine rule. See the article on the cosine rule for more information. You could also use the sine rule to prove that the two triangles are equiangular. See the article on the sine rule for more information on how to do this.

All Three Pairs of Sides in the Same Ratio

We often abbreviate this test by SSS (short for side-side-side)

This test says that two triangles in which all three pairs of corresponding sides are in the same ratio are similar.

Let's apply it to an example.

Example

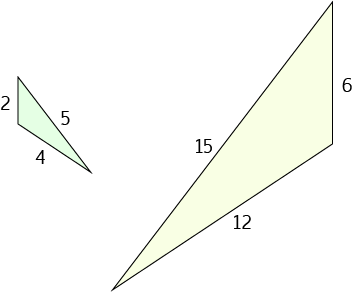
In the green and yellow triangles on the left:

• The longest pair of marked sides are in the ratio \(5:15 = 1:3\) (green:yellow)
• The next longest pair of marked sides are in the ratio \(4:12 = 1:3\) (green:yellow)
• The shortest pair of marked sides are in the ratio \(2:6 = 1:3\) (green:yellow)

So, the two triangles are similar since all three pairs of corresponding sides are in the same ratio (SSS).

It isn't necessary, but if you wanted to prove that the three pairs of corresponding angles of these triangles were equal, you could use the cosine rule. See the article on the cosine rule for a description of how to use the side-lengths of a triangle to find the angles in the triangle.