Year 10+ Plane Geometry
Chapters
Circles
Circles
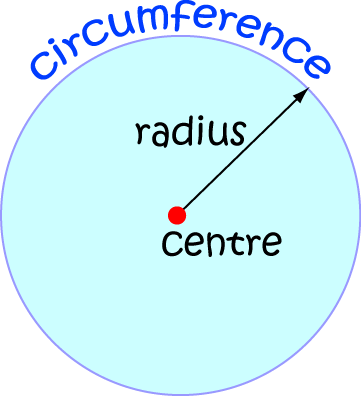
What is a circle? We all have a pretty good idea: it's something that's perfectly round. It has a centre, and the outside rim is called the circumference.
Every point on the circumference is the same distance away from the centre, and that distance is called the radius.
Formally, mathematicians define a circle to be the locus of a point which moves so that it is a fixed distance away (called the radius)
from a fixed point called the centre.
When we think about circles, we tend to think about a plane (flat) shape that includes the outside rim (or circumference) and all the points inside it.
Drawing Circles
If you try to draw a circle without any aids, you are doomed to failure. You can never make it "round" enough. Circles drawn like this always end up looking a bit squashed, or don't quite meet up. Luckily, there are some things we can use to draw a circle.
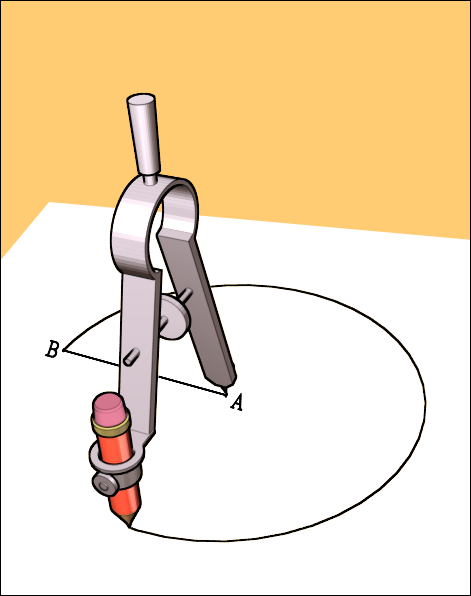
If you have a pair of compasses and a pencil, you're set. Insert the pencil into the pencil holder, open your compasses out to the desired radius, stick the pointy end of your compasses into your piece of paper (this will be the centre) and swing the pencil around, making sure the pointy end of the compasses stays in the same place. Hey presto! A perfect circle.
If you don't have a pair of compasses, you can still draw a circle using some objects that you're likely to have around the house. You'll need a piece of string, a pencil and a drawing pin as well as your paper. Here's what you do:
- Cut off a piece of string about twice as long as you want the radius of your circle to be, and tie it into a loop.
- Stick the drawing pin into your piece of paper where you want the centre of your circle to be.
- Put your loop of string over the pin, and insert your pencil into the loop.
- Pull the loop tight and swing your pencil around (touching the paper) to draw the circle.
Radius, Diameter and Circumference

The radius of a circle is the fixed distance measured from the centre of the circle to its perimeter.
The diameter of a circle is equal to twice its radius. A circle has zillions of diameters. They are the line segments that pass from one
point on the perimeter, through the centre of the circle, to another point on the perimeter.
The circumference is the special name we give to the perimeter of a circle. Its length is equal to the distance you would travel if you
walked around the edge of the circle once.
When we divide the circumference of a circle by the length of its diameter, we always get the same number, no matter how big or small the circle is.
That answer is the number we call \(\pi\) (pronounced "Pi"). We can't exactly write \(\pi\) down as it is what we call an irrational number. This means
that we can't write it as a decimal that either repeats or stops. However, people are finding more digits of \(\pi\) all the time. Here are some of them:
All of this gives us the following formulas for the circumference of a circle:
Example
Find the circumference of a circle with radius \(50 \text{ m}\).
Solution:
Using the formula,
Area of a Circle
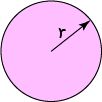
The area of a circle is equal to \(\pi\) times the square of the radius. We usually write the radius as \(r\) to give:
\(\text{Area} = \pi r^2\)
Remembering This

The area of a circle is equal to \(\pi\) times the square of the radius. We usually write the radius as \(r\) to give:
Here's a rhyme that Sam's maths teacher taught him when he was in Year 9 to help him remember the formulas for the area and circumference of a circle:
Twinkle, Twinkle, Little Star
Circumference equals 2 Pi r
Don't be frightened, don't be scared
Area equals Pi r squared.
Example
Find the area of a circle with radius \(50 \text{ m}\).
Solution:
Using the formula,
Circle Trivia: Comparing the Area of a Circle to the Area of a Square
The Ancient Greeks tried to construct a square with the same area as a circle using only a pair of compasses and a straight edge. It turns out that this is impossible.
If you draw a circle with the same diameter as the side-length of a square, the area of your circle will end up being about \(80\%\) of the area of the square. The exact value is \(\dfrac{\pi}{4}\%\).
Circle Terminology
It turns out that circles have fascinated mathematicians for thousands of years. As with anything that fascinates mathematicians for even an hour, special terminology has grown up around certain line segments related to circles and certain parts of circles. Let's have a look at some of it.
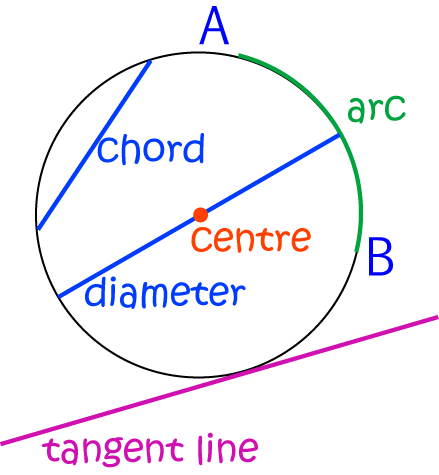
There are quite a few special line segments associated with circles.
A chord is a line segment that passes from one point on the circumference of a circle to another point on the circumference of the circle.
If a chord passes through the centre of the circle, we get all excited and call it a diameter
We call half a diameter (a line segment that goes from the centre of the circle to the circumference) a radius
A line that touches the circumference of a circle at one point (and stays entirely outside the circle apart from that point) is called a
tangent to the circle. The Ancient Greeks loved proving theorems about tangents to circles.
It isn't really a line segment, because its curved, but part of the circumference of a circle is called an arc.
Bits of a Circle
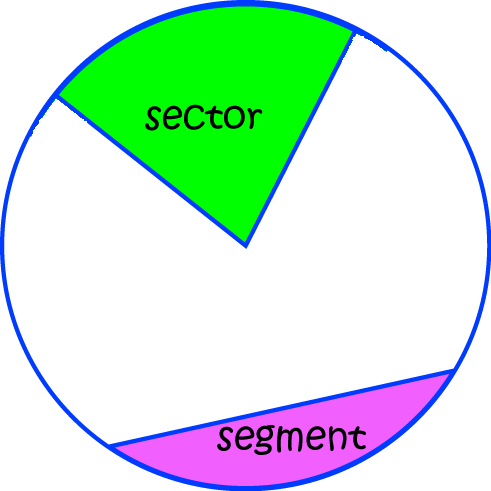
There are two main parts of a circle that we are interested in:
- A
sectoris shaped like a slice of cake - it's wedge-shaped and continues all the way out from the centre of the circle to the circumference. - A
segmentis a bit cut off the circle by a chord (a line that joins two points on the circumference of the circle).
Semicircles and Quadrants
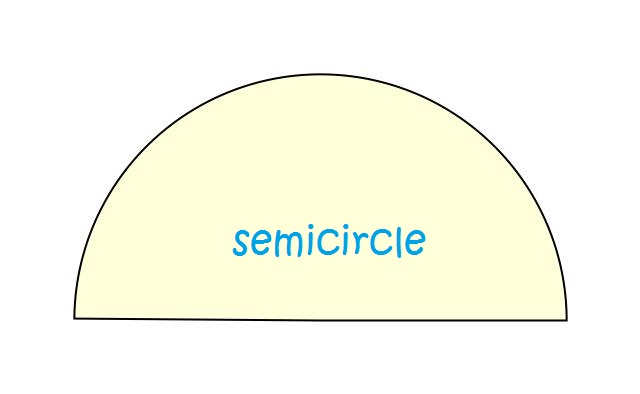
A semicircle is half of a circle. It is the sector which forms an angle of \(180^\circ\) (or \(\pi \text{ radians}\)) at the centre of the circle.
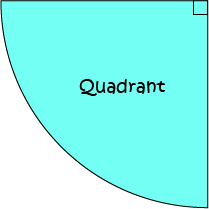
A quadrant is a quarter of a circle. It is the sector which forms an angle of \(90^\circ\) (or \(\dfrac{\pi}{2} \text{ radians}\)) at the centre of the circle.
Position Relative to a Circle
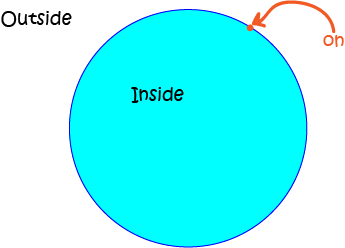
Have you ever done the "Hokey-Pokey"? In the "Hokey-Pokey" you put "your hand in" (putting it inside the ring you're standing on) and you put "your hand out" (putting it outside the ring you're standing on). When your hand is neither "in" nor "out", it must be "on" the ring you're standing on.
Just like in the "Hokey-Pokey" we can talk about points being inside, outside and on a circle. Let's see this on the picture below:
Conclusion
So that's everything you need to know, but were too afraid to ask, about circles in general. Other articles will explore the equations of circles, and the properties of sectors and segments.
Description
In these chapters you will learn about plane geometry topics such as
- Area (Irregular polygons, plane shapes etc)
- Perimeter
- Conic sections (Circle, Ellipse, Hyperbola etc)
- Polygons (Congruent, polygons, similar, triangles etc)
- Transformations and symmetry (Reflection, symmetry, transformations etc)
etc
Even though these chapters are marked for Year 10 or higher students, several topics are for students in Year 8 or higher
Audience
Year 10 or higher, suitable for Year 8 + students as well.
Learning Objectives
Learn about Plane Geometry
Author: Subject Coach
Added on: 28th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!