A pentagram (also known as a pentangle or a star pentagon) is a geometric shape that looks like a 5 pointed star. It is drawn using five straight line segments.

The pentagram was originally used as a symbol in ancient Greece and Babylon. The early Christians adopted the pentagram symbol, and it has also been used in Taoism and Islam, as shown on the Moroccan flag. Many people think of it as a symbol of witchcraft, but this is not entirely true.

The pentagram is one of the star polygons.

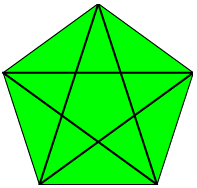
You can draw a pentagram by extending the edges of a pentagon until they intersect externally. You can also draw a pentagram inside a pentagon by joining up the vertices internally as shown in the picture on the left.

The picture on the right shows that each pentagram contains a pentagon (not necessarily blue). So, this means that you could (theoretically) draw an infinite sequence of pentagrams, nested, one inside the other, and you could extend it outwards as well. Pretty amazing, isn't it? This might be the reason for the pentagram's supposedly mystical properties.

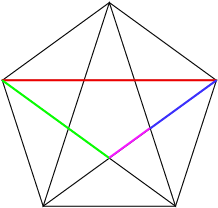
The ratios between the various coloured side lengths shown on this pentagram is supposed to equal the golden ratio (\(1.618\dots\)). I measured the coloured side lengths of this pentagram to be \(\text{red}=76\) mm, \(\text{green}= 46.5\) mm, \(\text{blue} = 29\) mm and \(\text{pink} = 18\) mm. I then calculated the ratios. The values I obtained were quite close to the golden ratio. Any differences are probably due to measurement and/or errors in drawing. Here are my ratios:

• \(\dfrac{\text{red}}{\text{green}} = 1.634\)
• \(\dfrac{\text{green}}{\text{blue}} = 1.603\)
• \(\dfrac{\text{blue}}{\text{pink}} = 1.611\)

Why don't you see if you can do better than I did? Draw yourself a regular pentagram, measure these distances, and calculate the ratios.