Reading:

Year 10+ Plane Geometry

Areas of Compound Shapes

Compound shapes are made up of two or more simple shapes. The area of a flat shape is the amount of space it takes up. In other words, it is the size of a surface.

Let's start by recalling the formulas for the areas of some plane shapes, and then look at a few examples of how these may be combined to find the areas of compound shapes.

Area Formulas for Simple Shapes

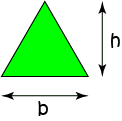
Triangle

$\text{Area} = \dfrac{1}{2} \times b \times h$

$b$ is the length of the base, and $h$ is the height of the triangle.

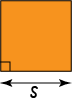
Square

$\text{Area} = s^2$

$s$ is the side-length of the square.

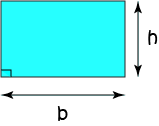
Rectangle

$\text{Area} = b \times h$

$b$ is the base (or length) of the rectangle.

$h$ is the height of the rectangle.

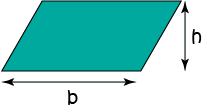
Parallelogram

$\text{Area} = b \times h$

$b$ is the base (or length) of the parallelogram.

$h$ is the height of the parallelogram.

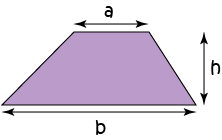
Trapezium

$\text{Area} = \dfrac{1}{2}(a + b) \times h$

$a$ and $b$ are the parallel sides of the trapezium.

$h$ is the height of the trapezium.

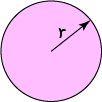
Circle

$\text{Area} = \pi r^2$

$r$ is the radius of the circle.

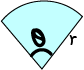
Sector

$\text{Area} = \dfrac{1}{2} \times r^2 \times \theta$

Note: for this to work, the angle must be measured in radians

Here, $r$ is the radius and $\theta$ is the angle at the centre, in radians.

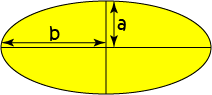
Ellipse

$\text{Area} = \pi ab$

$a$ and $b$ are half the lengths of the axes of the ellipse.

Note: In the above, the height is always perpendicular to the base of the shape.

Example 1

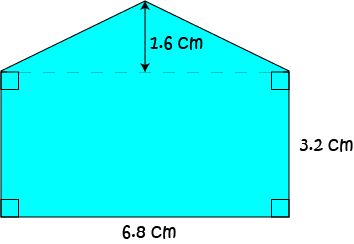
What is the area of the region that is coloured blue in the picture?

Solution:

This compound shape is made up of a rectangle of base-length 6.8 cm and height 3.2 cm, and a triangle of base-length 6.8 cm and height 1.6 cm. Its area is

$ \begin{align*} \text{Area} &= \text{Area Rectangle} + \text{Area Triangle}\\ &= b_{\text{rectangle}} \times h_{\text{rectangle}} + \dfrac{1}{2} b_{\text{triangle}}\times h_{\text{triangle}}\\ &= 6.8 \times 3.2 + \dfrac{1}{2} (6.8)(1.6)\\ &= 21.76 + 5.44\\ &= 27.2 \text{ cm}^2 \end{align*}$

Example 2

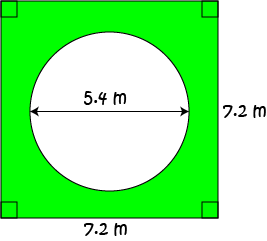
What is the area of the region that is coloured green in the picture?

Solution:

This compound shape is made up of a square of side-length 7.2 m from which a circle of diameter 5.4 m has been cut out. The radius of the circle is $r = 5.4 \div 2 = 2.7 \text{ m}$. Its area is

$ \begin{align*} \text{Area} &= \text{Area Square} - \text{Area Circle}\\ &= (\text{side-length})^2 - \pi r^2\\ &= (7.2)^2 - \pi (2.7)^2\\ &\approx 28.94 \text{ m}^2 \end{align*}$

Example 3

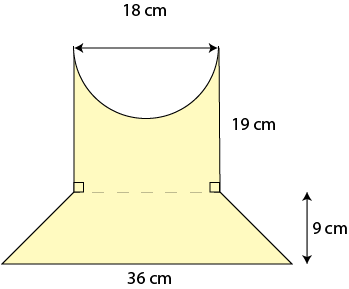
What is the area of the region that is coloured yellow in the picture?

Solution:

This compound shape is made up of a rectangle of side-lengths 19 cm and 18 cm from which a semicircle of diameter 18 cm has been cut out, together with a trapezium of parallel side-lengths 36 cm and 18 cm, and height 9 cm. The radius of the semicircle is $r = 18 \div 2 = 9 \text{ cm}$. Its area is

$ \begin{align*} \text{Area} &= \text{Area Rectangle} - \text{Area Semicircle} + \text{Area Trapezium}\\ &= b_{\text{rectangle}}h_{\text{rectangle}} - \dfrac{1}{2}\pi r^2 + \dfrac{h_{\text{trapezium}}}{2}(a + b) \\ &= 19 \times 18 - \dfrac{1}{2}\pi (9)^2 + \dfrac{9}{2}(18 + 36)\\ &\approx 457.77 \text{ cm}^2 \end{align*}$

One Last Example

Sam has a part-time job, mowing the oval-shaped park shown below.

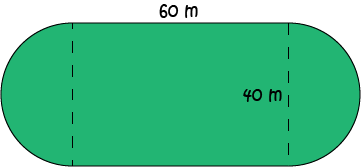
If he is paid $\$0.02$ per square metre mown, how much does he earn each time he mows the park?

Solution: We need to find the area of the oval in square metres and multiply it by $\$0.02$ to find Sam's earnings.

The oval is made up of two straight sides of length $60$ m, and two semi-circles of radius $\dfrac{1}{2}(40) = 20 \text{ m}$. So, its area is equal to the area of a circle of radius $20$ m, plus the area of a rectangle with base length $60$ m and height $40$ m:

$ \begin{align*} \text{Area} &= \pi r^2 + b \times h\\ &= \pi (20)^2 + (60)(40)\\ &= 400 \pi + 2,400 \text{ m}^2\\ &\approx 3656.64 \text{ m}^2. \end{align*} $

So, Sam is paid

$ \text{Wage} = 3656.64 \times 0.02 = \$73.13 $

for the job.

Description

In these chapters you will learn about plane geometry topics such as

Area (Irregular polygons, plane shapes etc)
Perimeter
Conic sections (Circle, Ellipse, Hyperbola etc)
Polygons (Congruent, polygons, similar, triangles etc)
Transformations and symmetry (Reflection, symmetry, transformations etc)

etc

Even though these chapters are marked for Year 10 or higher students, several topics are for students in Year 8 or higher

Audience

Year 10 or higher, suitable for Year 8 + students as well.

Learning Objectives

Learn about Plane Geometry

Author: Subject Coach
Added on: 28th Sep 2018

You must be logged in as Student to ask a Question.

None just yet!

Year 10+ Plane Geometry

Chapters

Areas of Compound Shapes

Areas of Compound Shapes

Area Formulas for Simple Shapes

Example 1

Example 2

Example 3

One Last Example

Description

Audience

Learning Objectives

THANK YOU FOR STOPPING BY!