Year 10+ Plane Geometry
Chapters
Exterior Angles of Polygons
Exterior Angles of Polygons
A polygon is any plane (flat) shape with straight edges. The exterior angles of polygons are the angles formed by any edge of the polygon and a line extended from the next edge of the polygon, as shown in the pictures
below:

interior angles of the polygon are the angles
inside the polygon between any two adjacent sides. A straight angle (\(180^\circ\)) is also marked. This is because the interior and exterior angles are angles along the same
straight line, and so they add up to \(180^\circ\). We call them
supplementary angles.
Examples
Let's look at a couple of examples in which we find exterior angles of polygons.
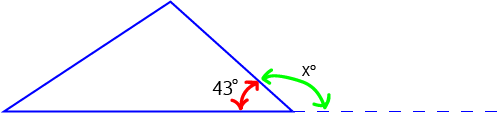
In this example, the interior angle corresponding to the exterior angle marked by the green arrow is \(43^\circ\). Since the exterior and interior angles at a given vertex must add up to \(180^\circ\), the exterior angle is \(180^\circ - 43^\circ = 137^\circ\). So, \(x = 137\).
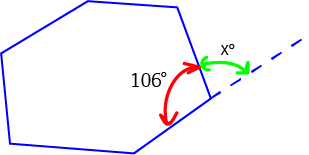
In this example, the interior angle corresponding to the exterior angle marked by the green arrow is \(106^\circ\). Since the exterior and interior angles at a given vertex must add up to \(180^\circ\), the exterior angle is \(180^\circ - 106^\circ = 74^\circ\). So, \(x = 74\).
The Sum of the Exterior Angles of a (Convex) Polygon
The exterior angles of a convex polygon (one with no dents) sum to \(360^\circ\)
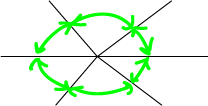
In the picture, we've joined all the exterior angles of a hexagon together. They take us right around the circle, forming a full revolution, so they add to \(360^\circ\). Note that this only works for convex polygons: ones with no dents.
Exterior Angles of Regular Polygons
All the interior angles of a regular polygon have the same size. Since the interior and exterior angles at a vertex of a polygon are supplementary, this means that all the exterior angles of a regular polygon are also equal. This is great, because it means we can find the size of the exterior angles of a regular polygon without knowing any of the interior angles. We simply divide \(360^\circ\) by the number of sides of the polygon. Once we know the size of the exterior angles, we can subtract it from \(180^\circ\) to find the size of the interior angles of the regular polygon. Let's look at an example.
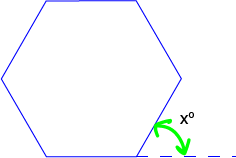
The hexagon in the picture is regular, so each of its exterior angles has the same size. We know that they add up to \(360^\circ\) as the regular hexagon is a convex polygon, and there are 6 of them because the hexagon has 6 sides. So, the size of each exterior angle is \(360 \div 6 = 60^\circ\), and \(x^\circ = 60^\circ\). Because the interior and exterior angles are supplementary, each interior angle of the hexagon is equal to \(180^\circ - 60^\circ = 120^\circ\).
Description
In these chapters you will learn about plane geometry topics such as
- Area (Irregular polygons, plane shapes etc)
- Perimeter
- Conic sections (Circle, Ellipse, Hyperbola etc)
- Polygons (Congruent, polygons, similar, triangles etc)
- Transformations and symmetry (Reflection, symmetry, transformations etc)
etc
Even though these chapters are marked for Year 10 or higher students, several topics are for students in Year 8 or higher
Audience
Year 10 or higher, suitable for Year 8 + students as well.
Learning Objectives
Learn about Plane Geometry
Author: Subject Coach
Added on: 28th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!