Year 10+ Plane Geometry
Chapters
Quadrilaterals
Quadrilaterals
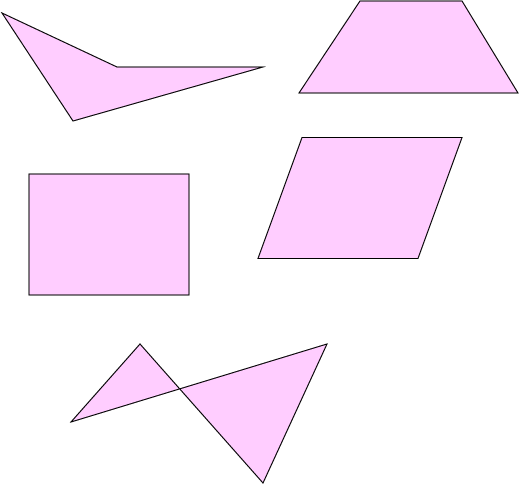
Quadrilaterals are plane (flat) shapes with 4 straight edges and 4 angles.
They are a type of polygon, so they need to be closed (the ends need to meet up).
Each quadrilateral has
- 4 straight edges
- 4 vertices (corners)
- An angle sum (sum of the interior angles) of \(360^\circ\).
The picture on the left shows a few different examples of quadrilaterals.
Some other names for quadrilaterals are quadrangles and tetragons.
Some More Examples
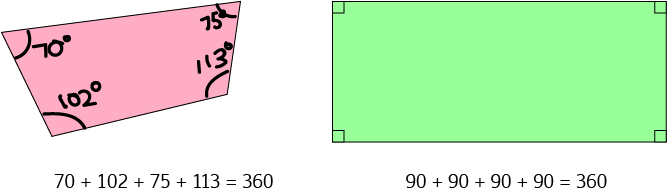
The sum of the angles in each of these quadrilaterals is \(360^\circ\) (don't forget that a right angle (marked by the little square in the green quadrilateral) is \(90^\circ\)).
There are a number of different special classes of quadrilaterals. They include rectangles, squares, rhombuses, parallelograms, kites and trapeziums. Let's have a look at each of these special types individually, and then we'll look at how they all fit together.
Rectangles

Rectangles have
- 2 pairs of opposite sides that are equal and parallel (one pair is marked in green on the diagram, and the other is red).
- 4 right angles
Squares
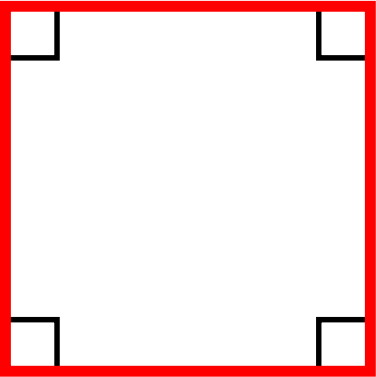
Squares have
- 2 pairs of opposite sides that are parallel.
- All sides equal in length.
- 4 right angles
Parallelograms

Parallelograms have
- 2 pairs of opposite sides that are equal and parallel (one pair is marked in green on the diagram, and the other is red).
- 2 pairs of opposite angles that are equal (one pair is marked green, and the other is marked red)
Rhombuses
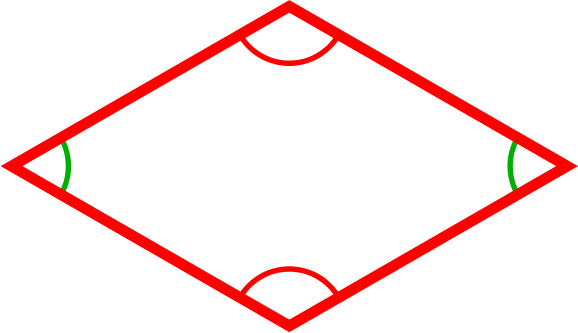
Rhombuses have
- 2 pairs of opposite sides that are parallel.
- 4 equal sides.
- 2 pairs of opposite angles that are equal (one pair is marked green, and the other is marked red)
Note: Rhombuses, squares and rectangles are all parallelograms. A rectangle is a parallelogram with one angle that is a right angle. A square is a parallelogram with all sides equal, and one angle a right angle. A rhombus is a parallelogram with all sides equal in length.
Trapeziums and Trapezoids
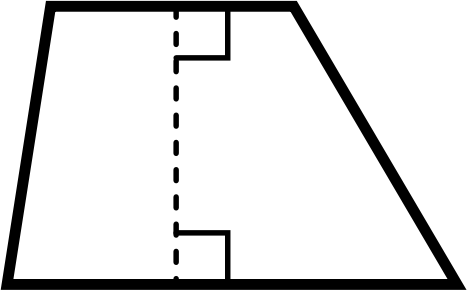
A trapezium is a quadrilateral that has
- One pair of opposite sides that is parallel.
isosceles trapezium also has two pairs of equal angles as shown in the diagram:
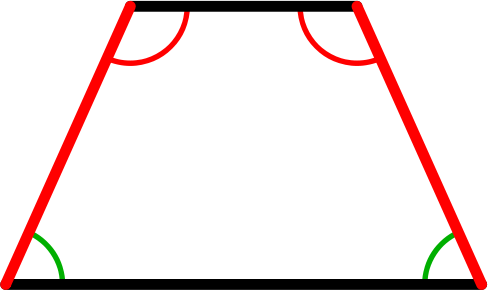
trapezoid is any old quadrilateral that has no parallel sides.
Fun Fact: If you do a web search for trapezoid, you'll find the definition of a trapezium, because people in the US and Canada call trapeziums trapezoids, and trapezoids trapeziums. The reason for this is due to an error in Hutton's Mathematical Dictionary, written in 1795, which was the first mathematical dictionary to appear in the US. Unfortunately, the error stuck, and now the definitions are reversed in North America.
Kites
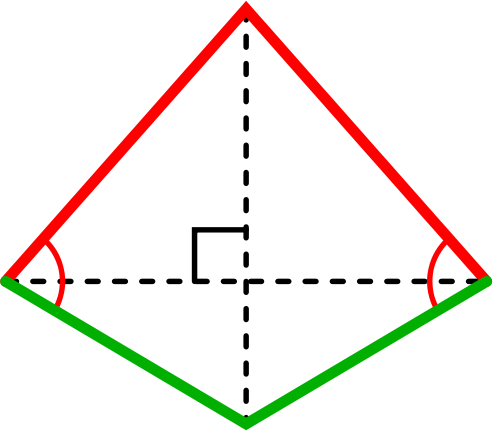
Kites have
- 2 pairs of adjacent sides that are equal (marked red and green on the diagram).
- Diagonals that intersect at right angles. One diagonal cuts the other one in half.
- One pair of equal and opposite angles.
Irregular Quadrilaterals
Every quadrilateral except for a square is an irregular quadrilateral, so there are plenty of them. Even though a rhombus has four equal sides, not all of its angles are equal.
Relationships Between Quadrilaterals
Squares are Rectangles, Rectangles and Squares are Parallelograms, Rhombuses and Parallelograms and so on. The diagram below shows you all the relationships between the different special quadrilaterals:
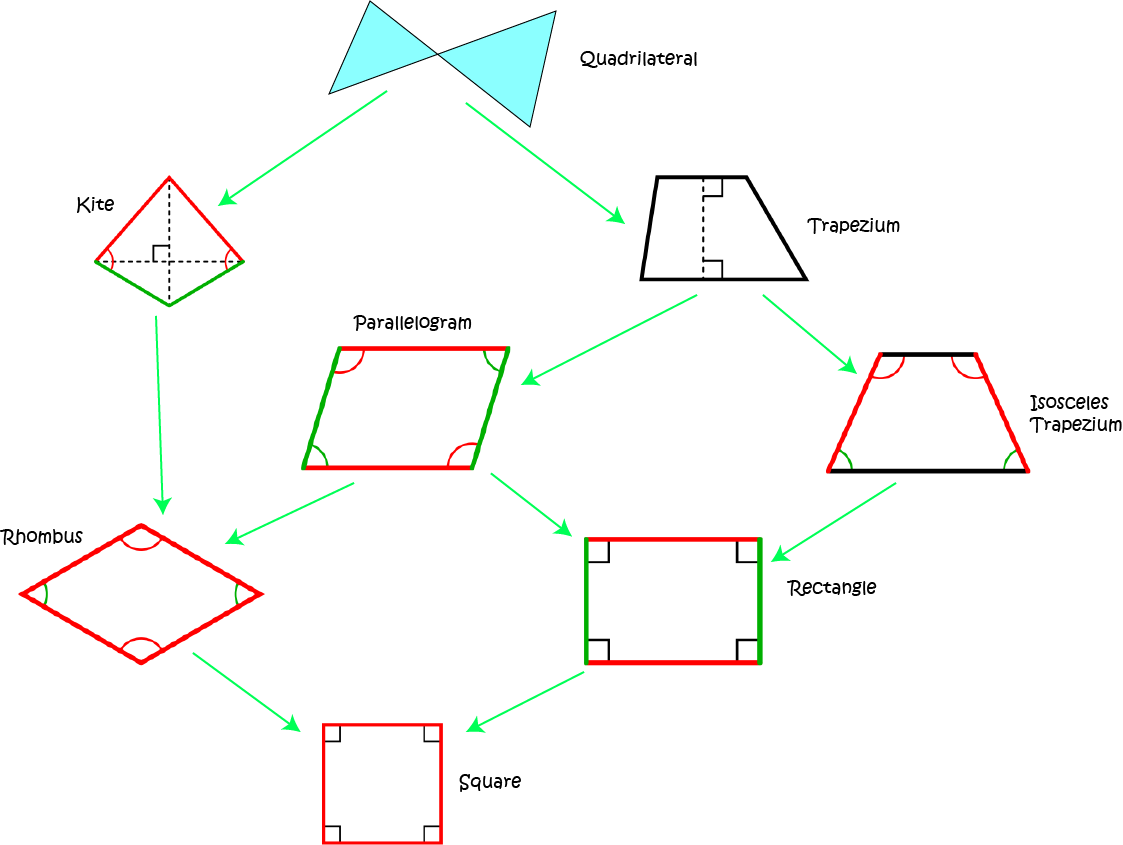
So, we can make the following statements:
- A parallelogram is a trapezium.
- A square is a rhombus.
- A rhombus is a kite.
Quadrilaterals Are Polygons
Quadrilaterals are 4-sided polygons. See the article on polygons for more information.
Just like polygons, quadrilaterals can be complex: this means that their sides can cross over like the ones in the diagram below.

Description
In these chapters you will learn about plane geometry topics such as
- Area (Irregular polygons, plane shapes etc)
- Perimeter
- Conic sections (Circle, Ellipse, Hyperbola etc)
- Polygons (Congruent, polygons, similar, triangles etc)
- Transformations and symmetry (Reflection, symmetry, transformations etc)
etc
Even though these chapters are marked for Year 10 or higher students, several topics are for students in Year 8 or higher
Audience
Year 10 or higher, suitable for Year 8 + students as well.
Learning Objectives
Learn about Plane Geometry
Author: Subject Coach
Added on: 28th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!