Polygons

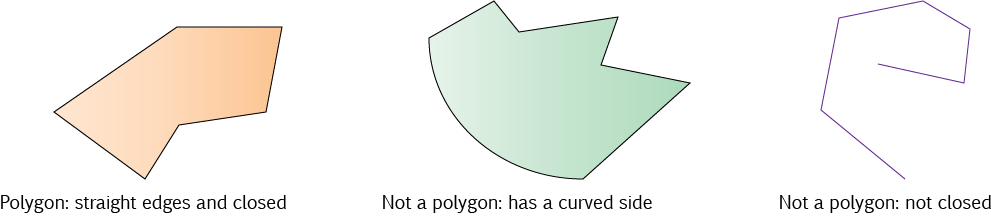
A polygon is any plane (flat) shape with straight edges.

How Do You Tell if It's a Polygon?

There are two things to check:

1. All the edges are straight
2. The shape is closed. That is, there aren't any gaps as the final edge ends where the first edge begins.

Top Secret Polygon Terminology

Well, maybe not. But here are some terms that are used to describe polygons.

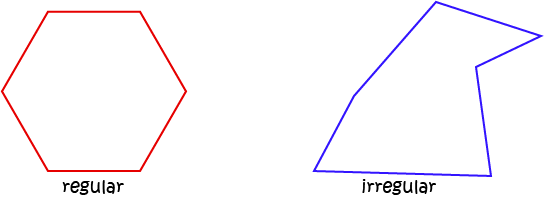
Regular and Irregular

In a regular polygon, all the edges have the same length and all the angles have the same size. In an irregular polygon, they don't.

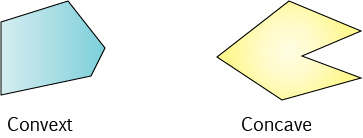
Concave and Convex

A convex polygon is one that doesn't have any dents in it: none of its interior angles are bigger than \(180^\circ\). A convex polygon looks a bit like a cave: it has at least one interior angle that is bigger than \(180^\circ\), so it has a dent in it.

Another way of thinking of this is that any line segment joining any two points inside a convex polygon stays entirely inside the polygon. You can find two points of a concave polygon that can't be joined by a line segment that stays entirely inside the polygon. See if you can find two points like this in the concave polygon in the picture below.

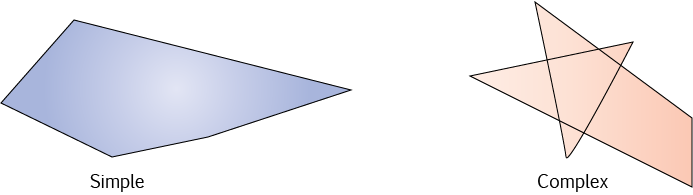
Simple and Complex

In a simple polygon, the edges only meet at the vertices (corner points). In a complex polygon, the edges can cross at points other than the vertices. Mathematicians say that a complex polygon intersects itself.

Lots of facts about polygons only work for simple polygons, so be careful about the facts you try to apply to complex polygons. In the pictures, the simple polygon is a pentagon (has 5 edges), and the complex polygon is a hexagon (has 6 edges).

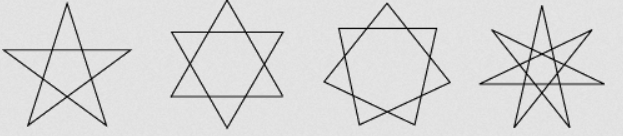
Star Polygons

Enough said, really. These are all complex pentagons. Here are a few of them:

Naming Polygons

There's a complex system of naming polygons available using all sorts of Greek prefixes. For example, you could call a 97-sided polygon a enneacontaheptagon if you really wanted to. However, once we get past about 12 sides, it really makes more sense to refer to a polygon with \(n\) sides as an \(n\)-gon. Let's have a look at the names of some common polygons, and the sizes of their interior angles.

Name of Polygon	Number of Sides	Picture	Interior Angles if Regular
Triangle	3		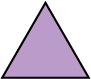\(60^\circ\)
Quadrilateral	4		\(90^\circ\)
Pentagon	5		\(108^\circ\)
Hexagon	6		\(120^\circ\)
Heptagon (or Septagon)	7		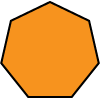\(128.57\dots^\circ\)
Octagon	8		\(135^\circ\)
Nonagon	9		\(140^\circ\)
Decagon	10		\(144^\circ\)
Hendecagon (or undecagon)	11		\(147.27^\circ\)
Dodecagon	12		\(150^\circ\)	Icosagon	20		\(162^\circ\)
30-gon	30		\(168^\circ\)
90-gon	90		\(176^\circ\)
1,000,000-gon	1,000,000		\(180^\circ\) (about)
n-gon	n		\(\dfrac{n}{n-2} \times 180^\circ\)

As the number of sides of a regular polygon gets larger, the interior angles get closer and closer to \(180^\circ\).

Polygons in Nature and Architecture

How many triangles can you spot in this stained glass ceiling? This ceiling is part of the National Gallery of Victoria in Melbourne.

The faces of salt crystals are shaped like quadrilaterals (squares).

Bees build the cells of their honeycomb in the shape of hexagons.

This, very originally named, building at the University of Heidelberg is called the Octagon Building.

Have a look around you and see if you can spot any more examples of polygons in nature, art or architecture. Have fun!