Areas of Polygons

In this article we're going to talk about a technique that can be used to program a computer to find the area of any polygon you like. The polygon can be regular (all sides and angles equal) or irregular. It really doesn't matter.

We'll work through the technique using this polygon:

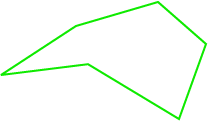
Step 1: Turn the Vertices into Coordinates

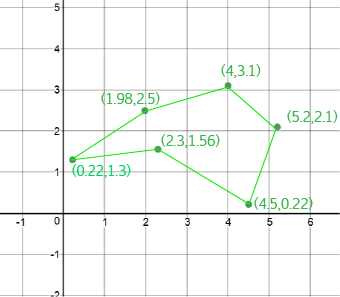
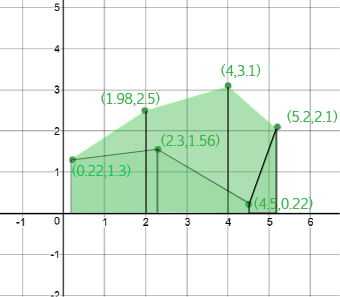
Essentially, we're going to plot the polygon in the \(xy\)-plane. Find \(xy\)-coordinates for each vertex:

Step 2: Find the Areas Under Each Line Segment

For each line segment (edge), we're going to work out the area between the edge and the \(x\)-axis. Here's a picture of one of them:

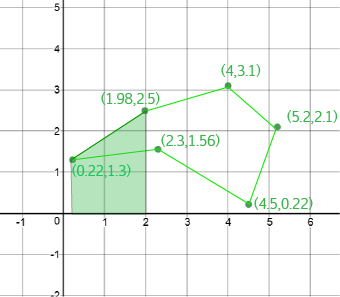
Do you see that the shape we need to find the area of is a trapezium? The lengths of the two parallel sides are the heights (or \(y\)-coordinates) of the vertices that form the end points of the line segment, and the height of the trapezium is the difference between the two \(x\)-coordinates of these points.

So that's the area of the first one. Next, we need to calculate all the others.

We always move clockwise around the polygon, and subtract the first vertex we come across as the end-point of a line segment away from the second vertex of the line segment. This will mean that some of the areas we calculate will be negative, but that's OK. I'll explain why in a little while. Here are the calculations:

Add up the Areas

Next we add up the areas under the line segments that we just found (make sure you keep track of the signs from the table, or you'll end up with an area that's too big.)

The area of the polygon is:

Why Do We Need Some of the Areas to be Negative?

If we add up the areas under the line segments at the top of the polygon (the ones we got positive areas for), we end up with the area shown below:

This is bigger than the area of the polygon. How much bigger? The area under the bottom line segments bigger! So, we need to take the areas under the bottom line segments away:

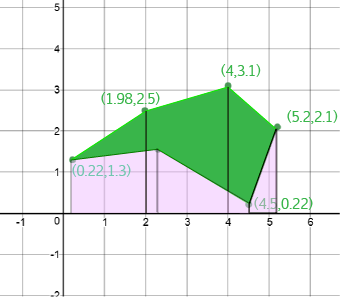
The area of our polygon is equal to the green area in the picture directly above, which is the same as the area shaded green on the first picture in this section minus the area shaded pink in the picture directly above. That's why some of our areas have to be negative.

This automatically happens when we walk around the shape clockwise, because the sides we walk along backwards are exactly the ones on the bottom of the polygon. That is, the ones that we need to take the areas away for.

Conclusion

So, that's it. You can use this technique to find the area of any polygon you like. The hardest part is finding the coordinates of the vertices. However, it is rather tedious, so if you know how, it's probably a good idea to program a computer to do all the calculations for you. Have fun!