Year 10+ Plane Geometry
Chapters
Ellipses
Ellipses
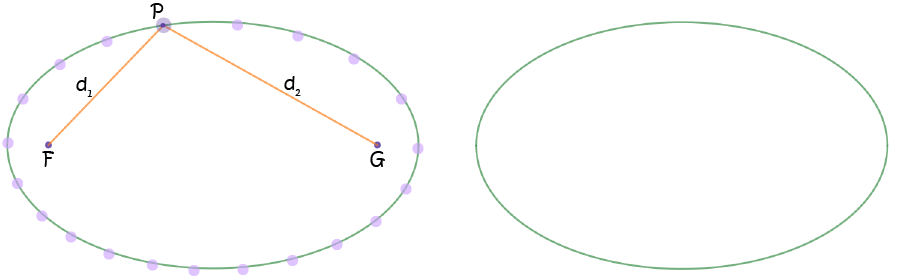
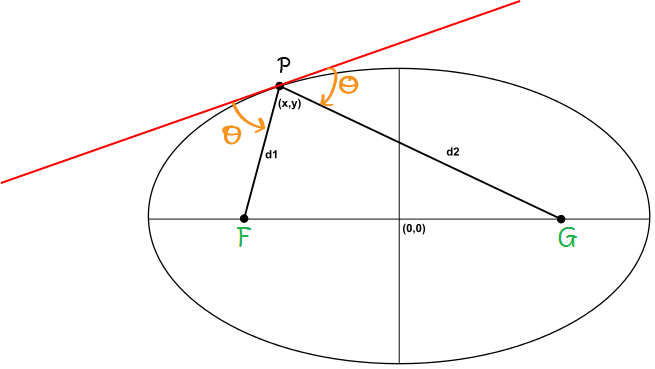
An ellipse is the locus of a point which moves so that the sum of its distances (\(d_1 + d_2\) in the diagram) from two fixed points called the foci
(F and G in the diagram is constant: \(d_1 + d_2 = \text{constant}\).
Ellipses look like squashed circles.
Drawing an Ellipse

Put a piece of paper on top of a board. Stick drawing pins into the paper at two points. Make a loop out of a piece of string, and place it around the two drawing pins.
Take your trusty pencil, put it inside the loop, and use it to stretch out the loop of string so that it forms a triangle.
Keeping the string stretched, draw a curve. Your pencil will trace out an ellipse.
If you only use one drawing pin, you get a circle. A circle is an ellipse in which the two foci are in the same place.
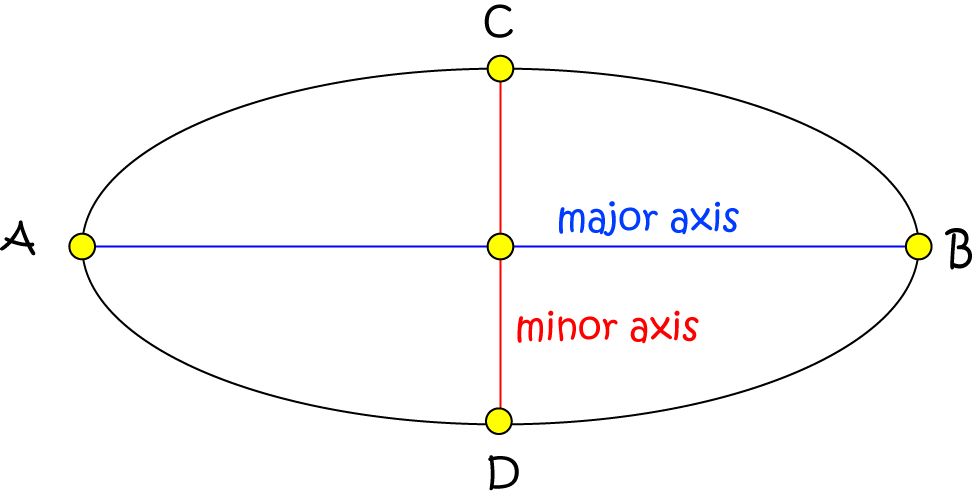
Axes of an Ellipse
The axes of an ellipse cut it in half. The major axis is the longest diameter of the ellipse, and the minor axis is the shortest diameter of the ellipse. Each passes through the centre of the ellipse.
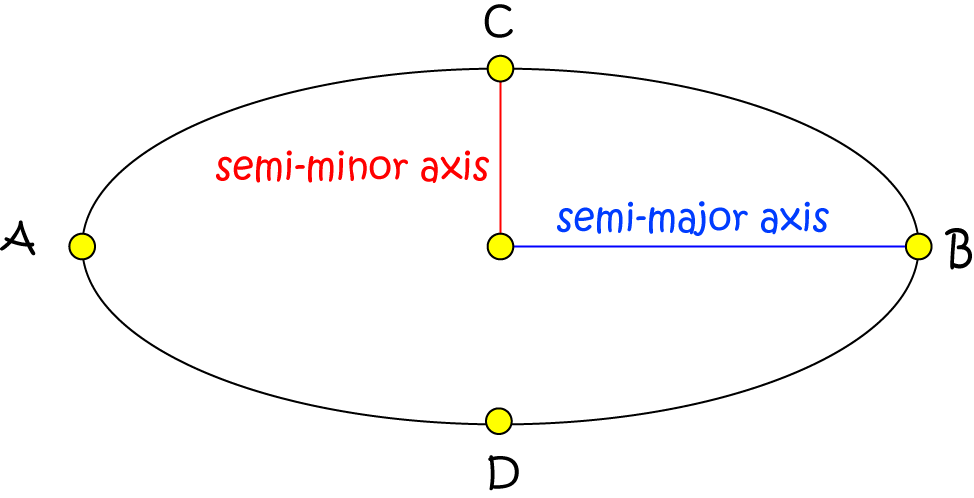
As their names suggest, the semi-major axis is half of the major axis of the ellipse, and the semi-minor axis is half of the minor axis
of the ellipse.
Area and Perimeter of an Ellipse
Area
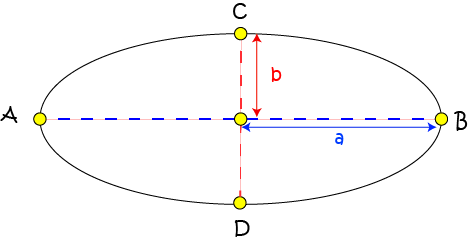
The formula for the area of an ellipse is exactly what you would expect: \(\text{Area} = \pi a b\), where \(a\) and \(b\) are the lengths of the semi-minor and semi-major axes. The formula for the area of a circle is a special case of this as both semi-major and semi-minor axes of a circle have the same length (the radius of the circle): \(\pi r^2\).
Perimeter
It is really, very, super hard to find the perimeter of an ellipse. I recommend taking that loop of string you used to draw your ellipse, untying the ends and using it, together with a ruler, to measure the perimeter of the ellipse.
For centuries, mathematicians have worked on finding simple approximations for the perimeter of the ellipse. There are exact formulas, but they involve adding up infinite series. The article on finding the perimeter of an ellipse explores some of these approximations. Here's an approximation that was recently found:
Tangents to Ellipses
A tangent is a line that touches a curve at a single point. There's an interesting result about the tangents to ellipses: the tangent at the point \(P\) forms equal angles with the lines joining each of the two foci of the ellipse to the point \(P\). Of course, the tangent to a circle at a point \(P\) is at right angles to the radius that ends at the point \(P\).
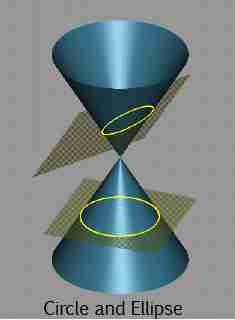
An Ellipse as a Conic Section
When you cut a slice through a cone, parallel to the base, you get a circle. When you slice through a cone, at a slight angle to the base, you get an ellipse.
This is why we say that ellipses are conic sections. The article on conic sections will tell you more about the other conic sections.
Each conic section is assigned a number, called the eccentricity, that tells you how close it is to being a circle. A circle has eccentricity \(0\), and the eccentricity of an ellipse is somewhere between \(0\) and \(1\).
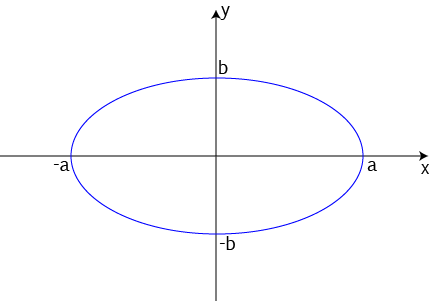
The Equation of an Ellipse
We can plot ellipses in the \(xy\)-plane. If we put the centre of the ellipse at the origin, its major axis along the \(x\)-axis, and its minor axis along the \(y\)-axis, then the equation of the ellipse is:
Here's the graph:
If you've read the article, or know about, hyperbolas, then you'll realise that this equation is similar to the equation of a hyperbola. The difference is that the equation for a hyperbola has a minus in the middle.
Description
In these chapters you will learn about plane geometry topics such as
- Area (Irregular polygons, plane shapes etc)
- Perimeter
- Conic sections (Circle, Ellipse, Hyperbola etc)
- Polygons (Congruent, polygons, similar, triangles etc)
- Transformations and symmetry (Reflection, symmetry, transformations etc)
etc
Even though these chapters are marked for Year 10 or higher students, several topics are for students in Year 8 or higher
Audience
Year 10 or higher, suitable for Year 8 + students as well.
Learning Objectives
Learn about Plane Geometry
Author: Subject Coach
Added on: 28th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!