Properties of Regular Polygons

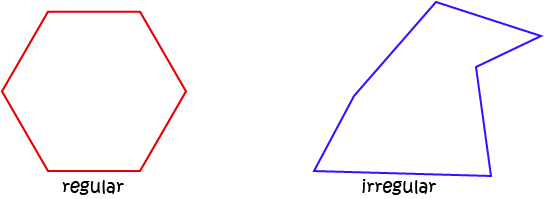
A polygon is any plane (flat) shape with straight edges.

A regular polygon is a polygon with

• All sides of equal length.
• All angles the same size.

Polygons that are not regular are called irregular

Exterior Angles of Polygons

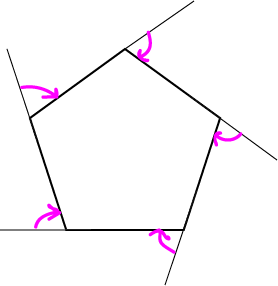
Exterior angles are angles that lie between a line extended from one edge of the polygon and the next edge (moving clockwise) as shown in the picture.

No matter how many sides a polygon has, its exterior angles add up to \(360^\circ\)

So, each exterior angle of a regular polygon with \(n\) sides is equal to

\(\dfrac{360^\circ}{n}\)

Example

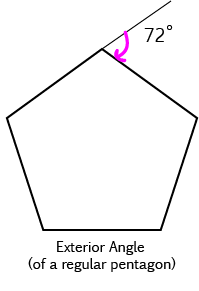
A pentagon has 5 sides, so each exterior angle of a regular pentagon is equal to

\(\dfrac{360^\circ}{5} = 72^\circ\)

Interior Angles of Polygons

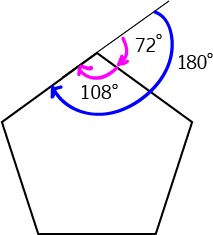
The interior angles are the ones inside the polygon between two adjacent edges. As the interior and exterior angles lie on the same straight line, they add up to \(180^\circ\).

Let's work out the sizes of the interior angles in a regular polygon with \(n\) sides:

Each Interior Angle \(= 180^\circ -\) Exterior Angle

Each Exterior Angle is

\(\dfrac{360^\circ}{n}\)

So each Interior Angle is

\(180^\circ - \dfrac{360^\circ}{n}\)

We can arrange this as follows:

\(\begin{align*} \text{Interior Angle} &= 180^\circ - \dfrac{360^\circ}{n} \\ &= \left(n \times \dfrac{180^\circ}{n}\right) - \left( 2 \times \dfrac{180^\circ}{n}\right)\\ &= (n - 2) \times \dfrac{180^\circ}{n} \end{align*} \)

So, each interior angle is equal to

\( (n - 2) \times \dfrac{180^\circ}{n}\)

Example

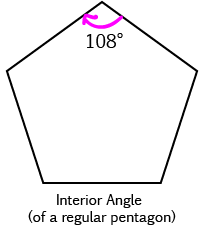
A pentagon has 5 sides, so each exterior angle of a regular pentagon is equal to

\(\dfrac{360^\circ}{5} = 72^\circ\)

and each interior angle is equal to

\(180^\circ - 72^\circ = 108^\circ\)

Alternatively, we could use the formula to find

\( \begin{align*} \text{Interior Angle} &= (n - 2) \times \dfrac{180^\circ}{n}\\ &= ( 5 - 2) \times \dfrac{180^\circ}{5}\\ &= 3 \times 36^\circ\\ &= 108^\circ \end{align*} \)

Example:

Find the interior and exterior angles of a regular decagon.

A decagon has 10 sides, so each exterior angle of a regular pentagon is equal to

\(\dfrac{360^\circ}{10} = 36^\circ\)

and each interior angle is equal to

\(180^\circ - 36^\circ = 144^\circ\)

Alternatively, we could use the formula to find

\( \begin{align*} \text{Interior Angle} &= (n - 2) \times \dfrac{180^\circ}{n}\\ &= ( 10 - 2) \times \dfrac{180^\circ}{10}\\ &= 8 \times 18^\circ\\ &= 144^\circ \end{align*} \)

Secret Regular Polygon Business

Not really secret, but there is special terminology associated with regular polygons that you may not have heard before.

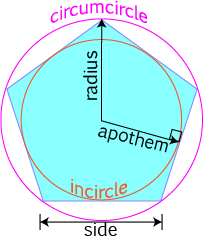
A circle drawn around a regular polygon that passes through all of its vertices is called a circumcircle. It is the smallest circle you can draw around a polygon.

The largest circle you can draw inside a regular polygon touches each side exactly once (at its midpoint). It is called an incircle.

The radius of the circumcircle is also called the radius of the polygon.

The radius of the incircle is called the apothem of the polygon.

Polygons and Triangles

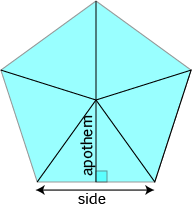
We can split a regular polygon with \(n\) sides up into \(n\) triangles as shown in the picture on the left.

The base of each triangle is equal to the side-length of the polygon.

The other two sides are equal to the radius of the polygon.

The height of each triangle is equal to the apothem of the polygon.

We can find the area of each triangle, and then multiply by \(n\) to give a formula for the area of the polygon:

\(\begin{align*} \text{Area of Triangle} &= \dfrac{1}{2} \; \text{base} \times \text{height}\\ &= \dfrac{1}{2}\;\text{side} \times \text{apothem} \end{align*} \)

So the area of the polygon is given by

\(\begin{align*} \text{Area of Polygon} &= n \times \text{Area of Triangle}\\ &= n \times \dfrac{1}{2}\;\text{side} \times \text{apothem}\\ &= \text{perimeter} \times \dfrac{1}{2} \times \text{apothem} \end{align*} \)

More Area Formulas

Each triangle is cut in half by the apothem:

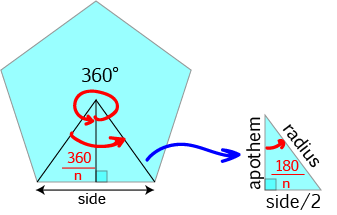
The smaller triangles formed like this are right-angled triangles because the apothem is the perpendicular bisector of the side of the polygon.

As the polygon can be split up into \(n\) triangles, the apex angle of the larger triangle is \(\dfrac{360^\circ}{n}\). So, the apex angle of the right-angled triangle is \(\dfrac{1}{2} \times \dfrac{360^\circ}{n} = \dfrac{180^\circ}{n}\).

We can use the right-angled trigonometric ratios to find relationships between the side, radius, apothem and \(n\) for the polygon.

• Using \(\sin \left(\dfrac{\pi}{n}\right) = \dfrac{\text{side}/2}{\text{radius}}\) gives \(\text{side} = 2 \times \text{radius} \times \sin \left(\dfrac{\pi}{n}\right)\).
• Using \(\cos \left(\dfrac{\pi}{n}\right) = \dfrac{\text{apothem}}{\text{radius}}\) gives \(\text{apothem} = \text{radius} \times \cos \left(\dfrac{\pi}{n}\right)\).
• Using \(\tan \left(\dfrac{\pi}{n}\right) = \dfrac{\text{side}/2}{\text{apothem}}\) gives \(\text{side} = 2 \times \text{apothem} \times \tan\left(\dfrac{\pi}{n}\right)\).

Using these relationships, we can find some more formulas for the area of the polygon.

If We Only Know the Apothem

The area of the smallest triangle is given by

From above, we know that

Since the whole polygon is made up of \(2n\) smaller triangles, the area of the polygon is given by

We can find other formulas involving only the radius or the side using a similar approach. They are:

We can find other formulas involving only the radius or the side using a similar approach. They are:

The table below shows the angle sums of polygons of various sizes, and the sizes of the interior angles of various polygons:

Name of Regular Polygon	Number of Sides	Picture	Interior Angles	Radius	Side	Apothem	Area
Equilateral Triangle	3		\(60^\circ\)	1	\(\sqrt{3} \approx 1.732\)	0.5	\(\dfrac{3}{4}\sqrt{3} \approx 1.299\)
Square	4		\(90^\circ\)	1	\(\sqrt{2} \approx 1.414\)	\(\dfrac{1}{\sqrt{2}} \approx 0.707\)	\(2\)
Pentagon	5		\(108^\circ\)	1	1.176	0.809	2.378
Hexagon	6		\(120^\circ\)	1	1	\(\dfrac{1}{2}\sqrt{3} \approx 0.866\)	\(\dfrac{3}{2} \sqrt{3} \approx 2.598\)
Heptagon (or Septagon)	7		\(128.57\dots^\circ\)	1	0.868	0.901	2.736
Octagon	8		\(135^\circ\)	1	0.765	0.924	2 \sqrt{2} \approx 2.828
Nonagon	9		\(140^\circ\)	1	0.684	0.940	2.893
Decagon	10		\(144^\circ\)	1	0.618	0.951	2.939

In general, as the number of sides becomes larger, and the radius is fixed at \(1\):

• The length of the sides gets smaller (approaches zero)
• The length of the apothem approaches 1 (which is the radius)
• The area of the polygon approaches \(\pi = 3.14159\dots\)

This is because, as we add in more sides, the polygon becomes more like a circle of radius 1, which has area \(\pi (1)^2 = \pi\). As the sides get shorter, the apothem gets closer and closer to the radius of the polygon (which is also the radius of the circle that the polygon is approaching).